推荐系统三十六式--学习笔记（11-13 矩阵分解）

11.【矩阵分解】那些在Netflix Prize中大放异彩的推荐算法

评分预测问题只是很典型，其实并不大众,数据难收集，属于精英问题。
行为预测，才是平民级推荐问题，处处可见。

缘起

评分预测问题之所以“虽然小众却十分重要”，这一点得益于十多年前 Netflix Prize 的那一百万美元的悬赏效应。

公元 2006 年 10 月 2 号，对于很多人来说，这只是平凡了无新意的一天，但对于推荐系统从业者来说，这是不得了的一天，美国著名的光盘租赁商 Netflix 突然广发英雄帖，放下“豪”言，这个就是土豪的“豪”，凡是能在他们现有推荐系统基础上，把均方根误差降低 10% 的大侠，可以瓜分 100 万美元。消息一出，群贤毕至。

最为著名的就是一系列矩阵分解模型，而最最著名的模型就是 SVD 以及其各种变体。

矩阵分解

为什么要矩阵分解

几点近邻模型的问题：

物品之间存在相关性，信息量并不随着向量维度增加而线性增加；
矩阵元素稀疏，计算结果不稳定，增减一个向量维度，导致近邻结果差异很大的情况存在。

矩阵分解，直观上说来简单，就是把原来的大矩阵，近似分解成两个小矩阵的乘积，在实际推荐计算时不再使用大矩阵，而是使用分解得到的两个小矩阵。

$U_{m \times k}V_{n \times k}^T \approx A_{m \times n}$

评分矩阵 A 是 m 乘以 n 维，即一共有 m 个用户，n 个物品。k 比 m 和 n 都小很多。这就是SVD，但是SVD 和矩阵分解不能划等号。

基础的 SVD 算法

SVD 全称奇异值分解，然而在推荐算法中实际上使用的并不是正统的奇异值分解，而是一个伪奇异值分解。

首先介绍基础的 SVD 算法，然后是考虑偏置信息，接着是超越评分矩阵增加多种输入，最后是增加时间因素。

矩阵分解，就是把用户和物品都映射到一个 k 维空间中，不一定具有非常好的可解释性，每一个维度也没有名字，所以常常叫做隐因子。举个例子，用户 u 的向量是 $p_u$，物品 i 的向量是 $q_i$，那么，要计算物品 i 推荐给用户 u 的推荐分数，直接计算点积即可：

$\hat r_{ui}=p_uq_i^T$

难在如何得到每一个用户，每一个物品的 k 维向量。需要考虑两个核心要素：

损失函数；
优化算法。

SVD 的损失函数是这样定义的：

$\min_{q^*,p^*}\sum_{(u,i)\in \mathcal K}(r_{ui}-p_uq_i^T)^2+\lambda (||q_i||^2+||p_u||^2)$

这个损失函数由两部分构成，加号前一部分控制着模型的偏差，加号后一部分控制着模型的方差。

前一部分就是：用分解后的矩阵预测分数，要和实际的用户评分之间误差越小越好。

整个 SVD 的学习过程就是（梯度下降（GD），另一个是交替最小二乘（ALS），这里以梯度下降为例）：

准备好用户物品的评分矩阵，每一条评分数据看做一条训练样本；

给分解后的 P 矩阵和 Q 矩阵随机初始化元素值；

用 P 和 Q 计算预测后的分数；

计算预测的分数和实际的分数误差；

按照梯度下降的方向更新 P 和 Q 中的元素值；

重复步骤 3 到 5，直到达到停止条件。

梯度下降算法的一个关键点在于计算损失函数对于每个参数的梯度。

$\frac{\partial}{\partial p_{uk}}e_{ui}^2=-2(r_{ui}-\sum_{k=1}^Kp_{uk}q_{ik})q_{ik}=-2e_{ui}q_{ik}$ $\frac{\partial}{\partial q_{ik}}e_{ui}^2=-2(r_{ui}-\sum_{k=1}^Kp_{uk}q_{ik})p_{uk}=-2e_{ui}p_{uk}$

求出了梯度之后，接下来是沿着负梯度的方向来更新每个参数。

$p_{uk} ：= p_{uk} - \alpha \frac{\partial }{\partial p_{uk}}e_{ui}^2 = p_{uk} + 2\alpha e_{ui}q_{ik}$ $q_{ik} ：= q_{ik} - \alpha \frac{\partial }{\partial q_{ik}}e_{ui}^2 = q_{ik} + 2\alpha e_{ui}p_{uk}$

其中, α 表示随机梯度的学习率。
在实际应用中，为了保证模型拥有更好的泛化效果，会在损失函数中加入 L2 正则化。

$e_{ui}^{2} = (r_{u,i} - \sum_{k=1}^{K}p_{uk}q_{ik})^{2} + \lambda \sum_{k=1}^{K}(p_{uk}^2 + q_{ik}^2)$

加入正则化之后，对损失函数求梯度，得到：

$\frac{\partial }{\partial p_{uk}}e_{ui}^2=-2\left ( r_{ui}-\sum_{k=1}^{K}p_{uk}q_{ik} \right )q_{ik} + 2 \lambda p_{uk} =-2e_{ui}q_{ik} + 2 \lambda p_{uk}$ $\frac{\partial }{\partial q_{ik}}e_{ui}^2=-2\left ( r_{ui}-\sum_{k=1}^{K}p_{uk}q_{ik} \right )p_{uk} + 2 \lambda q_{ik} = -2e_{ui}p_{uk} + 2 \lambda q_{ik}$

沿着负梯度的方向来更新每个参数：

$p_{uk} := p_{uk} - \alpha \frac{\partial }{\partial p_{uk}}e_{ui}^2 = p_{uk} + 2\alpha (e_{ui}q_{ik} - \lambda p_{uk} )$ $q_{ik} := q_{ik} - \alpha \frac{\partial }{\partial q_{ik}}e_{ui}^2 = q_{ik} + 2\alpha (e_{ui}p_{uk} - \lambda q_{ik})$

2 增加偏置信息

有一些用户会给出偏高的评分，比如标准宽松的用户；有一些物品也会收到偏高的评分，比如一些目标观众为铁粉的电影，甚至有可能整个平台的全局评分就偏高,评分 = 兴趣 + 偏见。所以，原装的 SVD 就有了第一个变种：把偏置信息抽出来的 SVD。

$\hat{r_{ui}} = \mu + b_{i} + b_{u} + p_{u}q_{i}^{T}$

从左往右，全局平均分、物品的评分偏置、用户评分的偏置、用户和物品之间的兴趣偏好。增加了偏置信息的 SVD 模型目标函数稍有改变：

$e_{ui}^{2} = (r_{u,i} - (\mu + b_{i} + b_{u} + \sum_{k=1}^{K}p_{uk}q_{ik}))^{2} + \lambda \left (\sum_{k=1}^{K}(p_{uk}^2 + q_{ik}^2) + b_{i}^{2} + b_{u}^{2}\right)$

和基本的 SVD 相比，要想学习两个参数：用户偏置和物品偏置。学习的算法还是一样的。

3 增加历史行为

有的用户评分比较少。事实上这很常见，相比沉默的大多数，主动点评电影或者美食的用户是少数。显式反馈比隐式反馈少，那么能不能利用隐式反馈来弥补这一点呢？另外，再考虑多一点，对于用户的个人属性，比如性别等。
在 SVD 中结合用户的隐式反馈行为和属性，这套模型叫做 SVD++。

隐式反馈加入的方法是：除了假设评分矩阵中的物品有一个隐因子向量外，用户有过行为的物品集合也都有一个隐因子向量，维度是一样的。把用户操作过的物品隐因子向量加起来，用来表达用户的兴趣偏好。

类似的，用户属性，全都转换成 0-1 型的特征后，对每一个特征也假设都存在一个同样维度的隐因子向量，一个用户的所有属性对应的隐因子向量相加，也代表了他的一些偏好。

评分=显式兴趣 + 隐式兴趣 + 偏见，此时的评分估计为：

$\hat{r_{ui}} = \mu + b_{i} + b_{u} + (p_{u} + |N(u)|^{-0.5} \sum_{i\in{N(u)}}{x_{i}}+\sum_{a\in A_u}y_{a})q_{i}^{T}$

学习的参数多了两个向量：x 和 y。一个是隐式反馈的物品向量，另一个用户属性的向量。

4 考虑时间因素

需要考虑的是：人是善变的。

在 SVD 中考虑时间因素，有几种做法：

对评分按照时间加权，让久远的评分更趋近平均值；

对评分时间划分区间，不同的时间区间内分别学习出隐因子向量，使用时按照区间使用对应的隐因子向量来计算；

对特殊的期间，如节日、周末等训练对应的隐因子向量。

12.【矩阵分解】Facebook是怎么为十亿人互相推荐好友的

回顾矩阵分解

矩阵分解两个矩阵有这么几个特点：

每个用户对应一个 k 维向量，每个物品也对应一个 k 维向量，就是所谓的隐因子向量，因为是无中生有变出来的，所以叫做“隐因子”；
两个矩阵相乘后，就得到了任何一个用户对任何一个物品的预测评分，具体这个评分靠不靠谱，那就是看功夫了。

在优化目标函数的时候，优化方法常用的选择有两个，一个是随机梯度下降（SGD），另一个是交替最小二乘（ALS）。在实际应用中，交替最小二乘更常用一些，这也是社交巨头 Facebook 在他们的推荐系统中选择的主要矩阵分解方法。

交替最小二乘原理 (ALS)

任务是找到两个矩阵 P 和 Q，让它们相乘后约等于原矩阵 R：

$R_{m \times n}=P_{m \times k} \times Q_{n \times k}^T$

难点在于P和Q均是位置的，如果知其一就可以接触另一个，例如，若一直Q：

$P_{m \times k} = R_{m \times n} \times Q_{n \times k}^{-1}$

于是我们可以通过交替最小二乘通过迭代的方式解决这个难题：

初始化随机矩阵 Q 里面的元素值；
把 Q 矩阵当做已知的，直接用线性代数的方法求得矩阵 P；
得到了矩阵 P 后，把 P 当做已知的，故技重施，回去求解矩阵 Q；

交替最小二乘有这么几个好处：

在交替的其中一步，也就是假设已知其中一个矩阵求解另一个时，要优化的参数是很容易并
行化的；
在不那么稀疏的数据集合上，交替最小二乘通常比随机梯度下降要更快地得到结果，事实上
这一点就是我马上要说的，也就是关于隐式反馈的内容。

隐式反馈

矩阵分解算法，是为解决评分预测问题而生的,相比“预测用户会打多少分”，“预测用户会不会去浏览”更加有意义。收集到的数据只有明确的一类：用户干了某件事，而用户明确“不干”某件事的数据却没有明确表达。所以这就是 One-Class 的由来，One-Class 数据也是隐式反馈的通常特点。

对隐式反馈的矩阵分解，需要将交替最小二乘做一些改进，改进后的算法叫做加权交替最小二乘：Weighted-ALS。也就是说，行为的次数是对行为的置信度反应，也就是所谓的加权。

加权交替最小二乘这样对待隐式反馈：

如果用户对物品无隐式反馈则认为评分是 0；

如果用户对物品有至少一次隐式反馈则认为评分是 1，次数作为该评分的置信度。

现在的目标函数在原来的基础上变成这样：

$\min_{q^*,p^*}\sum_{(u,i)\in \mathcal K}c_{ui}(r_{ui}-p_uq_i^T)^2+\lambda (||q_i||^2+||p_u||^2)$

多出来的 $c_{ui}$ 就是置信度，在计算误差时考虑反馈次数，次数越多，就越可信。置信度一般也不是直接等于反馈次数，根据一些经验，置信度 $c_{ui}$ 这样计算：

$c_{ui}=1 + \alpha C$

阿尔法是一个超参数，需要调，默认值取 40 可以得到差不多的效果，C 就是次数了。

注：那些没有反馈的缺失值，就是在我们的设定下，取值为 0 的评分就非常多，有两个原因导致在实际使用时要注意这个问题：

本身隐式反馈就只有正类别是确定的，负类别是我们假设的，你要知道，One-Class 并不是随便起的名字；

这会导致正负类别样本非常不平衡，严重倾斜到 0 评分这边。

不能使所有的缺失值作为负类别，矩阵分解的初心就是要填充这些值，如果都假设他们为 0 了，那就忘记初心了。应对这个问题的做法就是负样本采样：挑一部分缺失值作为负类别样本即可。怎么挑？有两个方法：

随机均匀采样和正类别一样多；
按照物品的热门程度采样。

第一种不是很靠谱，第二种在实践中经过了检验。

按照物品热门程度采样的思想就是：一个越热门的物品，用户越可能知道它的存在。那这种情况下，用户还没对它有反馈就表明：这很可能就是真正的负样本。

13.【矩阵分解】如果关注排序效果，那么这个模型可以帮到你

矩阵分解在推荐系统中的地位非常崇高，恐怕本专栏介绍的其他算法模型都不能轻易地撼动它。

矩阵分解的不足

得到这样的矩阵分解结果后，常常在实际使用时，又是用这个预测结果来排序。在排序学习中的行话叫做 point-wise，其中 point 意思就是：只单独考虑每个物品，每个物品像是空间中孤立的点一样。与之相对的，还有直接预测物品两两之间相对顺序的问题，就叫做 pair-wise，pair，顾名思义就是成对比较。

前面讲的矩阵分解都属于 point-wise 模型。这类模型的尴尬是：只能收集到正样本，没有负样本，于是认为缺失值就是负样本，再以预测误差为评判标准去使劲逼近这些样本。虽然进行了负样本采样来优化，但还是出现不好的负样本。

更直接的推荐模型应该是：能够较好地为用户排列出更好的物品相对顺序，而非更精确的评分。贝叶斯个性化排序，简称 BPR 模型。

贝叶斯个性化排序

均方根误差，用于评价模型预测精准程度的。那么现在要关注的是相对排序，用什么指标比较好呢？答案是 AUC，AUC 全称是 Area Under Curve，意思是曲线下的面积，这里的曲线就是 ROC 曲线。

ROC曲线

二分类预测的混淆矩阵：

—	Truth Positive	Truth Negative	Sum
Estimate Positive	TP	FP	$N_+$=TP+FP
Estimate Negative	FN	TN	$N_-$=FN+TN
Sum	$N_+$=TP+FN	$N_-$=FP+TN	N=TP+FP+FN+TN

真正例率（True Positive Rate , TPR）：

$TPR=\frac{TP}{N_+} \approx p(\hat y=1|y=1)$

假正例率(False Positive Rate , FPR):

$FPR=\frac{FP}{N_-} \approx p(\hat y=1|y=0)$

TPR-FPR的相关图就是ROC曲线：

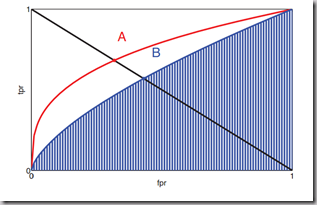
AUC

AUC 这个值在数学上等价于：模型把关心的那一类样本排在其他样本前面的概率。最大是 1，完美结果，而 0.5 就是随机排列，0 就是完美地全部排错。

AUC的计算步骤：

用模型给样本计算推荐分数，比如样本都是用户和物品这样一对一对的，同时还包含了有无反馈的标识；

得到打过分的样本，每条样本保留两个信息，第一个是分数，第二个是 0 或者 1，1 表示用户消费过，是正样本，0 表示没有，是负样本；

按照分数对样本重新排序，降序排列；

给每一个样本赋一个排序值，第一位 $r_1 = n$，第二位 $r_2 = n-1$，以此类推；其中要注意，如果几个样本分数一样，需要将其排序值调整为他们的平均值；

终按照下面这个公式计算就可以得到 AUC 值。 $AUC=\frac {\sum_{i\in (sample)r_i-\frac{M \times (M+1)}{2}}}{M \times N}$ 公式两部分构成：
第一部分：分母是所有我们关心的那类样本，也就是正样本，有 M 个，以及其他样本有 N 个，这两类样本相对排序总共的组合可能性，是 M x N；
第二部分：分子也不复杂，原本是这样算的：第一名的排序值是 $r_1$，它在排序上不但比过了所有的负样本，而且比过了自己以外的正样本。但后者是自己人，所以组合数要排除，于是就有 n - M 种组合，以此类推，排序值为 $r_M$ 的就贡献了 $r_M$ - 1，把这些加起来就是分子。

BPR 模型，它提出了一个优化准则和学习框架,主要有三点：

一个样本构造方法；
一个模型目标函数；
一个模型学习框架。
通过这三步可以脱离评分预测，来做专门优化排序的矩阵分解。

构造样本

前面介绍的矩阵分解，在训练时候处理的样本是：用户、物品、反馈，这样的三元组形式。其中反馈又包含真实反馈和缺失值，缺失值充当的是负样本职责。BPR 则不同，提出要关心的是物品之间对于用户的相对顺序，于是构造的样本是：用户、物品 1、物品 2、两个物品相对顺序，这样的四元组形式。

其中，“两个物品的相对顺序”，取值是：

如果物品 1 是消费过的，而物品 2 不是，那么相对顺序取值为 1，是正样本；

如果物品 1 和物品 2 刚好相反，则是负样本；

样本中不包含其他情况：物品 1 和物品 2 都是消费过的，或者都是没消费过的。

目标函数

BPR 怎么完成矩阵分解，依然需要像交替最小二乘那样的思想。先假装矩阵分解结果已经有了，于是就计算出用户对于每个物品的推荐分数，只不过这个推荐分数可能并不满足均方根误差最小，而是满足物品相对排序最佳。
那么对于四元组中两个产品的预测分数的差定为：$X_{u12}$。表示的是对用户 u，物品 1 和物品 2 的矩阵分解预测分数差。然后再用 sigmoid 函数把这个分数差压缩到 0 到 1 之间。

$\Theta = \frac {1}{1+e^{-(X_{u12})}}$

其实就是用这种方式预测了物品 1 排在物品 2 前面的似然概率，所以最大化交叉熵就是目标函数了。

目标函数通常还要防止过拟合，加上正则项，正则项其实认为模型参数还有个先验概率，这是贝叶斯学派的观点，也是 BPR 这个名字中“贝叶斯”的来历。BPR 认为模型的先验概率符合正态分布，对应到正则化方法就是 L2 正则:

$\prod_{u,i,j}p(i>_u j|\theta)p(\theta)$

所有样本都计算：模型参数先验概率$p(\theta)$，和似然概率的乘积，最大化这个目标函数就能够得到分解后的矩阵参数，其中 $\theta$ 就是分解后的矩阵参数。把这个目标函数化简和变形后，和把 AUC 当成目标函数是非常相似的，也正因为如此，BPR 模型的作者敢于宣称该模型是为 AUC 而生的。

训练方法

首选梯度下降，但又有批量梯度和随机梯度下降两个选择，前者收敛慢，后者训练快却不稳定。因此 BPR 的作
者使用了一个介于两者之间的训练方法，结合重复抽样的梯度下降。具体来说是这样做的：

从全量样本中有放回地随机抽取一部分样本；

用这部分样本，采用随机梯度下降优化目标函数，更新模型参数；

重复步骤 1，直到满足停止条件。

矩阵分解