稀疏矩阵(Sparse Matrix)

1 背景

在企业的深度学习项目中，Sparse稀疏矩阵这个词想必大家都不陌生。在模型的矩阵计算中，往往会遇到矩阵较为庞大且非零元素较少。由其是现在深度学习中embedding大行其道，稀疏矩阵成为必不可少的基建。而这种情况下，如果依然使用dense的矩阵进行存储和计算将是极其低效且耗费资源的。Sparse稀疏矩阵就称为了救命稻草。在拜读多篇优秀博客后，这里做一些自己的汇总和填补。

2 稀疏矩阵

2.1 定义

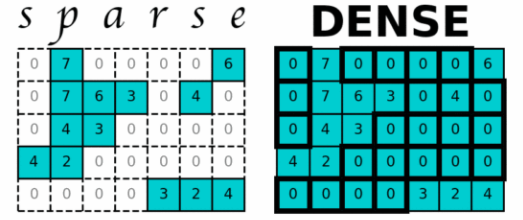
sparseMatrix1

如上所示，一般当矩阵非零项较少的时候，就称为非零矩阵，也即其中只有少量的有用信息-非零项。

那么可以做一个更为书面的定义：
具有少量非零项的矩阵 - Number of Non-Zero (NNZ) < 0.5

在矩阵中，若数值0的元素数目远多于非0元素的数目，并且非0元素分布没有规律。

矩阵的稠密度

非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。

2.2 压缩存储

存储矩阵的一般方法是采用二维数组，其优点是可以随机地访问每一个元素，因而能够容易实现矩阵的各种运算，如转置运算、加法运算、乘法运算等。

对于稀疏矩阵，它通常具有很大的维度，有时甚大到整个矩阵（零元素）占用了绝大部分内存，采用二维数组的存储方法既浪费大量的存储单元来存放零元素，又要在运算中浪费大量的时间来进行零元素的无效运算。因此必须考虑对稀疏矩阵进行压缩存储（只存储非零元素）。

我们可以通过python的scipy包看到一些压缩方式：

from scipy import sparse
help(sparse)

'''
Sparse Matrix Storage Formats
There are seven available sparse matrix types:

        1. csc_matrix: Compressed Sparse Column format
        2. csr_matrix: Compressed Sparse Row format
        3. bsr_matrix: Block Sparse Row format
        4. lil_matrix: List of Lists format
        5. dok_matrix: Dictionary of Keys format
        6. coo_matrix: COOrdinate format (aka IJV, triplet format)
        7. dia_matrix: DIAgonal format
        8. spmatrix: Sparse matrix base clas
'''

其中一般较为常用的是csc_matrix，csr_matrix和coo_matrix。

2.3 一些属性和通用方法

我们还是以python的scipy包为例，来介绍一些稀疏矩阵的属性和通用方法。

稀疏属性

from scipy.sparse import csr_matrix

### 共有属性
mat.shape  # 矩阵形状
mat.dtype  # 数据类型
mat.ndim  # 矩阵维度
mat.nnz   # 非零个数
mat.data  # 非零值, 一维数组

### COO 特有的
coo.row  # 矩阵行索引
coo.col  # 矩阵列索引

### CSR\CSC\BSR 特有的
bsr.indices    # 索引数组
bsr.indptr     # 指针数组
bsr.has_sorted_indices  # 索引是否排序
bsr.blocksize  # BSR矩阵块大小

通用方法

import scipy.sparse as sp

### 转换矩阵格式
tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil()
mat.toarray()  # 转为array
mat.todense()  # 转为dense
# 返回给定格式的稀疏矩阵
mat.asformat(format)
# 返回给定元素格式的稀疏矩阵
mat.astype(t)  

### 检查矩阵格式
issparse、isspmatrix_lil、isspmatrix_csc、isspmatrix_csr
sp.issparse(mat)

### 获取矩阵数据
mat.getcol(j)  # 返回矩阵列j的一个拷贝，作为一个(mx 1) 稀疏矩阵 (列向量)
mat.getrow(i)  # 返回矩阵行i的一个拷贝，作为一个(1 x n)  稀疏矩阵 (行向量)
mat.nonzero()  # 非0元索引
mat.diagonal()   # 返回矩阵主对角元素
mat.max([axis])  # 给定轴的矩阵最大元素

### 矩阵运算
mat += mat     # 加
mat = mat * 5  # 乘
mat.dot(other)  # 坐标点积

3 常用压缩方法

3.1 COO

全称是Coordinate Matrix对角存储矩阵，这里是官方文档。

定义详解

采用三元组(row, col, data)(或称为ijv format)的形式来存储矩阵中非零元素的信息;

三个数组 row 、col 和 data 分别保存非零元素的行下标、列下标与值（一般长度相同;

故 coo[row[k]][col[k]] = data[k] ，即矩阵的第 row[k] 行、第 col[k] 列的值为 data[k];

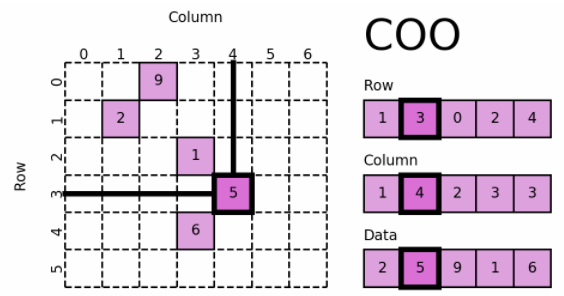
sparseMatrix2

适用场景

主要用来创建矩阵，因为coo_matrix无法对矩阵的元素进行增删改等操作
一旦创建之后，除了将之转换成其它格式的矩阵，几乎无法对其做任何操作和矩阵运算

优点

转换成其它存储格式很快捷简便（tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil()）
能与CSR / CSC格式的快速转换
允许重复的索引（例如在1行1列处存了值2.0，又在1行1列处存了值3.0，则转换成其它矩阵时就是2.0+3.0=5.0）

缺点

不支持切片和算术运算操作
如果稀疏矩阵仅包含非0元素的对角线，则对角存储格式(DIA)可以减少非0元素定位的信息量
这种存储格式对有限元素或者有限差分离散化的矩阵尤其有效

属性

data：稀疏矩阵存储的值，是一个一维数组
row：与data同等长度的一维数组，表征data中每个元素的行号
col：与data同等长度的一维数组，表征data中每个元素的列号

code case

# 数据
row = [0, 1, 2, 2]
col = [0, 1, 2, 3]
data = [1, 2, 3, 4]

# 生成coo格式的矩阵
# <class 'scipy.sparse.coo.coo_matrix'>
coo_mat = sparse.coo_matrix((data, (row, col)), shape=(4, 4),  dtype=np.int)

# coordinate-value format
print(coo)
'''
(0, 0)        1
(1, 1)        2
(2, 2)        3
(3, 3)        4
'''

# 查看数据
coo.data
coo.row
coo.col

# 转化array
# <class 'numpy.ndarray'>
coo_mat.toarray()
'''
array([[1, 0, 0, 0],
       [0, 2, 0, 0],
       [0, 0, 3, 4],
       [0, 0, 0, 0]])
'''

3.2 CSR

全称是Compressed Sparse Row Matrix压缩稀疏行格式，这里是官方文档。

定义详解

csr_matrix是按行对矩阵进行压缩的
通过 indices, indptr，data 来确定矩阵。
data 表示矩阵中的非零数据
对于第 i 行而言，该行中非零元素的列索引为 indices[indptr[i]:indptr[i+1]]
可以将 indptr 理解成利用其自身索引 i 来指向第 i 行元素的列索引
根据[indptr[i]:indptr[i+1]]，我就得到了该行中的非零元素个数，如
1. 若 index[i] = 3 且 index[i+1] = 3 ，则第 i 行的没有非零元素
2. 若 index[j] = 6 且 index[j+1] = 7 ，则第 j 行的非零元素的列索引为 indices[6:7]
得到了行索引、列索引，相应的数据存放在： data[indptr[i]:indptr[i+1]]

sparseMatrix3

构造方法

对于矩阵第 0 行，我们需要先得到其非零元素列索引
1. 由 indptr[0] = 0 和 indptr[1] = 2 可知，第 0 行有两个非零元素。
2. 它们的列索引为 indices[0:2] = [0, 2] ，且存放的数据为 data[0] = 8 ， data[1] = 2
3. 因此矩阵第 0 行的非零元素 csr[0][0] = 8 和 csr[0][2] = 2
对于矩阵第 4 行，同样我们需要先计算其非零元素列索引
1. 由 indptr[4] = 3 和 indptr[5] = 6 可知，第 4 行有3个非零元素。
2. 它们的列索引为 indices[3:6] = [2, 3，4] ，且存放的数据为 data[3] = 7 ，data[4] = 1 ，data[5] = 2
3. 因此矩阵第 4 行的非零元素 csr[4][2] = 7 ， csr[4][3] = 1 和 csr[4][4] = 2

适用场景
常用于读入数据后进行稀疏矩阵计算，运算高效。

优点

高效的稀疏矩阵算术运算
高效的行切片
快速地矩阵矢量积运算

缺点

较慢地列切片操作（可以考虑CSC）
转换到稀疏结构代价较高（可以考虑LIL，DOK）

属性

data ：稀疏矩阵存储的值，一维数组
indices ：存储矩阵有有非零值的列索引
indptr ：类似指向列索引的指针数组
has_sorted_indices：索引 indices 是否排序

code case

# 生成数据
indptr = np.array([0, 2, 3, 3, 3, 6, 6, 7])
indices = np.array([0, 2, 2, 2, 3, 4, 3])
data = np.array([8, 2, 5, 7, 1, 2, 9])

# 创建矩阵
csr = sparse.csr_matrix((data, indices, indptr))

# 转为array
csr.toarray()
'''
array([[8, 0, 2, 0, 0],
       [0, 0, 5, 0, 0],
       [0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0],
       [0, 0, 7, 1, 2],
       [0, 0, 0, 0, 0],
       [0, 0, 0, 9, 0]])
'''

3.3 CSC

全称是Compressed Sparse Column Matrix压缩稀疏列矩阵，这里是官方文档。

定义详解

csc_matrix是按列对矩阵进行压缩的
通过 indices, indptr，data 来确定矩阵，可以对比CSR
data 表示矩阵中的非零数据
对于第 i 列而言，该行中非零元素的行索引为indices[indptr[i]:indptr[i+1]]
可以将 indptr 理解成利用其自身索引 i 来指向第 i 列元素的列索引
根据[indptr[i]:indptr[i+1]]，我就得到了该行中的非零元素个数，如
1. 若 index[i] = 1 且 index[i+1] = 1 ，则第 i 列的没有非零元素
2. 若 index[j] = 4 且 index[j+1] = 6 ，则第 j列的非零元素的行索引为 indices[4:6]
得到了列索引、行索引，相应的数据存放在： data[indptr[i]:indptr[i+1]]

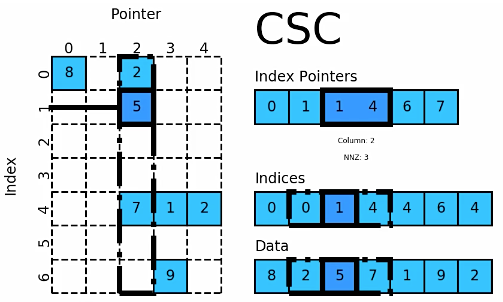
sparseMatrix4

构造方法

对于矩阵第 0 列，我们需要先得到其非零元素行索引
1. 由 indptr[0] = 0 和 indptr[1] = 1 可知，第 0列行有1个非零元素。
2. 它们的行索引为 indices[0:1] = [0] ，且存放的数据为 data[0] = 8
3. 因此矩阵第 0 行的非零元素 csc[0][0] = 8
对于矩阵第 3 列，同样我们需要先计算其非零元素行索引
1. 由 indptr[3] = 4 和 indptr[4] = 6 可知，第 4 行有2个非零元素。
2. 它们的行索引为 indices[4:6] = [4, 6] ，且存放的数据为 data[4] = 1 ，data[5] = 9
3. 因此矩阵第 i 行的非零元素 csr[4][3] = 1 ， csr[6][3] = 9

应用场景和优缺点基本上与CSR互相对应。

特殊属性

data ：稀疏矩阵存储的值，一维数组
indices ：存储矩阵有有非零值的行索引
indptr ：类似指向列索引的指针数组
has_sorted_indices ：索引是否排序

code case

# 生成数据
row = np.array([0, 2, 2, 0, 1, 2])
col = np.array([0, 0, 1, 2, 2, 2])
data = np.array([1, 2, 3, 4, 5, 6])

# 创建矩阵
csc = sparse.csc_matrix((data, (row, col)), shape=(3, 3)).toarray()

# 转为array
csc.toarray()
'''
array([[1, 0, 4],
       [0, 0, 5],
       [2, 3, 6]], dtype=int64)
'''

# 按col列来压缩
# 对于第i列，非0数据行是indices[indptr[i]:indptr[i+1]] 数据是data[indptr[i]:indptr[i+1]]
# 在本例中
# 第0列，有非0的数据行是indices[indptr[0]:indptr[1]] = indices[0:2] = [0,2]
# 数据是data[indptr[0]:indptr[1]] = data[0:2] = [1,2],所以在第0列第0行是1，第2行是2
# 第1行，有非0的数据行是indices[indptr[1]:indptr[2]] = indices[2:3] = [2]
# 数据是data[indptr[1]:indptr[2] = data[2:3] = [3],所以在第1列第2行是3
# 第2行，有非0的数据行是indices[indptr[2]:indptr[3]] = indices[3:6] = [0,1,2]
# 数据是data[indptr[2]:indptr[3]] = data[3:6] = [4,5,6],所以在第2列第0行是4，第1行是5,第2行是6

3.4 BSR

全称是Block Sparse Row Matrix分块压缩稀疏行格式，这里是官方文档。

定义详解

基于行的块压缩，与csr类似，都是通过data，indices，indptr来确定矩阵
与csr相比，只是data中的元数据由0维的数变为了一个矩阵（块），其余完全相同
块大小 blocksize
1. 块大小 (R, C) 必须均匀划分矩阵 (M, N) 的形状。
2. R和C必须满足关系：M % R = 0 和 N % C = 0
3. 适用场景及优点参考csr

特殊属性

data ：稀疏矩阵存储的值，一维数组
indices ：存储矩阵有有非零值的列索引
indptr ：类似指向列索引的指针数组
blocksize ：矩阵的块大小
has_sorted_indices：索引 indices 是否排序

code case

# 生成数据
indptr = np.array([0,2,3,6])
indices = np.array([0,2,2,0,1,2])
data = np.array([1,2,3,4,5,6]).repeat(4).reshape(6,2,2)

# 创建矩阵
bsr = bsr_matrix((data, indices, indptr), shape=(6,6)).todense()

# 转为array
bsr.todense()
matrix([[1, 1, 0, 0, 2, 2],
        [1, 1, 0, 0, 2, 2],
        [0, 0, 0, 0, 3, 3],
        [0, 0, 0, 0, 3, 3],
        [4, 4, 5, 5, 6, 6],
        [4, 4, 5, 5, 6, 6]])

3.5 LIL

全称是Linked List Matrix链表矩阵格式，这里是官方文档。

定义详解

使用两个列表存储非0元素data
rows保存非零元素所在的列
可以使用列表赋值来添加元素，如 lil[(0, 0)] = 8

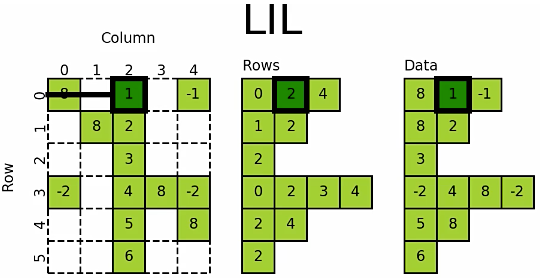
sparseMatrix5

构造方法

lil[(0, -1)] = 4 ：第0行的最后一列元素为4
lil[(4, 2)] = 5 ：第4行第2列的元素为5

适用场景

适用的场景是逐渐添加矩阵的元素（且能快速获取行相关的数据）
需要注意的是，该方法插入一个元素最坏情况下可能导致线性时间的代价，所以要确保对每个元素的索引进行预排序

优点

适合递增的构建成矩阵
转换成其它存储方式很高效
支持灵活的切片

缺点

当矩阵很大时，考虑用coo
算术操作，列切片，矩阵向量内积操作慢

属性

data：存储矩阵中的非零数据
rows：存储每个非零元素所在的列（行信息为列表中索引所表示）

code case

# 创建矩阵
lil = sparse.lil_matrix((6, 5), dtype=int)

# 设置数值
# set individual point
lil[(0, -1)] = -1
# set two points
lil[3, (0, 4)] = [-2] * 2
# set main diagonal
lil.setdiag(8, k=0)

# set entire column
lil[:, 2] = np.arange(lil.shape[0]).reshape(-1, 1) + 1

# 转为array
lil.toarray()
'''
array([[ 8,  0,  1,  0, -1],
       [ 0,  8,  2,  0,  0],
       [ 0,  0,  3,  0,  0],
       [-2,  0,  4,  8, -2],
       [ 0,  0,  5,  0,  8],
       [ 0,  0,  6,  0,  0]])
'''

# 查看数据
lil.data
'''
array([list([0, 2, 4]), list([1, 2]), list([2]), list([0, 2, 3, 4]),
       list([2, 4]), list([2])], dtype=object)
'''
lil.rows
'''
array([[list([8, 1, -1])],
       [list([8, 2])],
       [list([3])],
       [list([-2, 4, 8, -2])],
       [list([5, 8])],
       [list([6])]], dtype=object)
'''

3.6 DIA

全称是Diagonal Matrix对角存储格式格式，这里是官方文档。

定义详解

最适合对角矩阵的存储方式
dia_matrix通过两个数组确定： data 和 offsets
data ：对角线元素的值
offsets ：第 i 个 offsets 是当前第 i 个对角线和主对角线的距离
data[k:] 存储了 offsets[k] 对应的对角线的全部元素

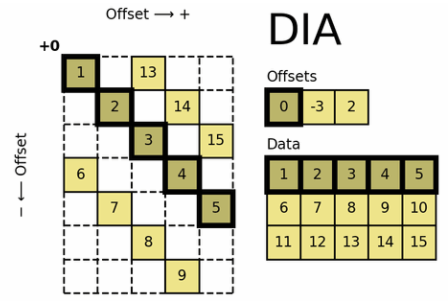
sparseMatrix6

构造方法

当 offsets[0] = 0 时，表示该对角线即是主对角线，相应的值为 [1, 2, 3, 4, 5]
当 offsets[2] = 2 时，表示该对角线为主对角线向上偏移2个单位，相应的值为 [11, 12, 13, 14, 15]
但该对角线上元素仅有三个，于是采用先出现的元素无效的原则
即前两个元素对构造矩阵无效，故该对角线上的元素为 [13, 14, 15]

属性

data：存储DIA对角值的数组
offsets：存储DIA对角偏移量的数组

code case

# 生成数据
data = np.array([[1, 2, 3, 4], [5, 6, 0, 0], [0, 7, 8, 9]])
offsets = np.array([0, -2, 1])

# 创建矩阵
dia = sparse.dia_matrix((data, offsets), shape=(4, 4))

# 查看数据
dia.data
'''
array([[[1 2 3 4]
        [5 6 0 0]
        [0 7 8 9]])
'''

# 转为array
dia.toarray()
'''
array([[1 7 0 0]
       [0 2 8 0]
       [5 0 3 9]
       [0 6 0 4]])
'''

参考文献
经典算法之稀疏矩阵
 Sparse稀疏矩阵主要存储格式总结
 20190624_稀疏矩阵存储及计算介绍
 sparse matrix 的分布式存储和计算