向量检索算法

1 基础知识

1.1 背景

在深度学习大兴的时代，embeding无处不在，不论是在搜索推荐领域还是cv领域亦或nlp领域。俗话说得好，万物皆可embeding，那么对于embeding化后的对象我们在做topk检索/召回的时候怎么提效呢？毕竟候选集往往都是在千万级或者亿级的时候，计算量是相当大的。这时候，向量检索算法就发挥了作用。在我理解的向量检索一般可以分为两个方向，一种是精确化检索，需要遍历每个样本，计算量往往很大，基本上被淘汰了。另一种就是近似检索，学术上对应的专有名词叫Approximate Nearest Neighbor Search (ANNS)，即近似最近邻搜索。为什么是近似，而不是我们想要的精确？这就是精度与时间、算力资源的折中，采用了牺牲精度换取时间和空间的方式，从海量的样本中实时获取跟查询最相似的样本。

1.2 向量距离

深度学习时代用的最多的就是embeding向量，而向量的基础形式往往就是一个数组，我们一般所需要的任务就是找出按照候选集中各个向量与目标向量的相似度倒排后的topK个。既然谈到向量之间的相似度，那么就要引入向量间的距离来进行刻画了。在实际中常用的向量距离主要有以下四种：

1. 欧式距离(Euclidean Distance)

   d_{12} = \sqrt{\sum_{k=1}^n(x_{1k}-x_{2k})^2}

   两点间的真实距离，值越小，说明距离越近；

2. 夹角余弦(Cosine)

   cos \theta = \frac{x_1x_2 + y_1y_2}{\sqrt{x_1^2 + y_1^2} \sqrt{x_2^2+y_2^2}}

   就是两个向量围成夹角的 cosine 值，cosine 值越大，越相似；

3. 汉明距离(Hamming distance)

   d(x,y)=\sum x_i \oplus y_i

   一般作用于二值化向量，二值化的意思是向量的每一列只有 0 或者 1 两种取值。汉明距离的值就两个向量每列数值的异或和，值越小说明越相似，一般用于图片识别；

4. 杰卡德相似系数(Jaccard similarity coefficient)

   J(A,B)=\frac{A \cap B}{A \cup B}

   把向量作为一个集合，所以它可以不仅仅是数字代表，也可以是其他编码，比如词，该值越大说明越相似，一般用于相似语句识别；

1.3 Brute Force

提到向量检索，最简单，最准确但最低效的方法就是 Brute Force，顾名思义，就是暴力比对每一条向量的距离。一般可以作为其他检索方法的baseline，尤其是独一召回率的参考。
值得一提的是阿里使用 BinaryDocValues 实现了 ES 上的 BF 插件。更进一步，要加速计算，所以使用了 JAVA Vector API 。JAVA Vector API 是在 openJDK project Panama 项目中的，它使用了 SIMD 指令优化。

import jdk.panama.vector.*;
import jdk.panama.vector.Vector.Shape;

Species = FloatVector.species(Shape.S_256_BIT);

// 求平方和
vecSquare = Species.broadcast(0);
for(i=0; i+(Species.length()) <+ size; i+= Species.length()){
    // 可以直接从byte数组计算，减少一步byte[]转floast[]
    vec = Species.fromByteArray(array, i>>2);
    vecSquare = vec.mul(vec).add(vecSquare);
    }
    sum = vecSquare.addAll();

使用 avx2 指令优化，100w 的 256 维向量，单分片比对，RT 在 260ms，是常规 BF 的 1/6。 ElasticSearch 官方在7.3版本也发布了向量检索功能，底层也是基于 Lucene 的 BinaryDocValues，并且它还集成入了 painless 语法中，使用起来更加灵活。

2 向量检索模型

一个高效的向量检索模型网网需要满足下面三个条件才能达到工业级可用：

• 实时查询，支持海量（百亿、千亿级别）规模库量级的；
• 存储高效，要求构建的向量索引模型数据压缩比高，达到大幅缩减内存使占用的目的；
• 召回精度好，top@K有比较好的召回率，跟暴力搜索（brute-force search）的结果相比；

前面提到向量检索按照思想可以分为精确检索和金丝检索，这里按照召回具体方法分为四大类：基于树的方法、哈希方法、矢量量化方法、图索引量化方法。

2.1 基于树的方法

KNN 算法表示的是准确的召回 topK 的向量，这里主要有两种算法，一种是 KDTtree，一种是 Brute Force。我们首先分析了 KDTree 的算法，发现 KDTree 并不适合高维向量召回。

2.1.1 KDTree 算法

简单来讲，就是把数据按照平面分割，并构造二叉树代表这种分割，在检索的时候，可以通过剪枝减少搜索次数。

构建树KD

树选择从哪一维度进行开始划分的标准，采用的是求每一个维度的方差，然后选择方差最大的那个维度开始划分。

为何要选择方差作为维度划分选取的标准？
我们知道，方差的大小可以反映数据的波动性。方差大表示数据波动性越大，选择方差最大作为划分空间标准的好处在于，可以使得所需的划分面数目最小，反映到树的数据结构上，可以使得我们构建的 KD 树的树深度尽可能小。

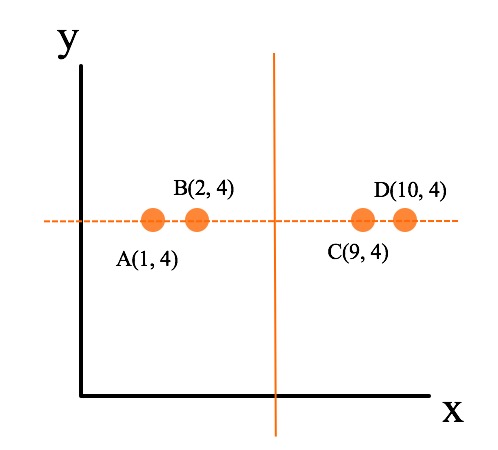
如上图为例，假设不以方差最大的x轴为划分面(x_var = 16.25)，而是以y轴(y_var = 0.0)轴为划分面，如图中虚线所示，可以看到，该划分使得图中的四个点都落入在同一个子空间中，从而使得该划分成为一个无效的划分，体现在以树结构上，就是多了一层无用的树深度。而以x轴为初始划分则不同(图像实线所示)，以x轴为初始划分可以得到数据能够比较均匀的散布在左右两个子空间中，使得整体的查找时间能够最短。注意，在实际的kd树划分的时候，并不是图中虚线所示，而是选取中值最近的点。

以二维平面点 (x,y) 的集合 (2,3),(5,4),(9,6),(4,7),(8,1),(7,2) 为例构建树：

1. 构建根节点时，x 维度上面的方差较大，如上点集合在 x 维从小到大排序为 (2,3)，(4,7)，(5,4)，(7,2)，(8,1)，(9,6)；
2. 其中值为 (7,2)。(2,3)，(4,7)，(5,4) 挂在 (7,2) 节点的左子树，(8,1)，(9,6) 挂在 (7,2) 节点的右子树。
3. 构建 (7,2) 节点的左子树时，点集合 (2,3)，(4,7)，(5,4) 此时的切分维度为 y，中值为 (5,4) 作为分割平面，(2,3) 挂在其左子树，(4,7) 挂在其右子树。
4. 构建 (7,2) 节点的右子树时，点集合 (8,1)，(9,6) 此时的切分维度也为 y，中值为 (9,6) 作为分割平面，(8,1) 挂在其左子树。

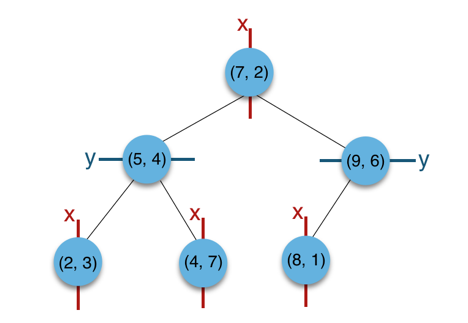
上述的构建过程结合下图可以看出，构建一个 KDTree 即是将一个二维平面逐步划分的过程。

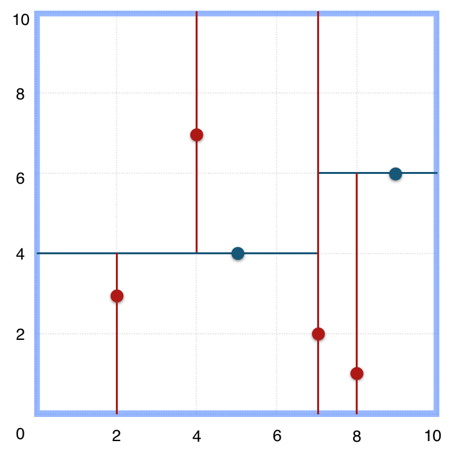
搜索 (3,5) 的最近邻

1. 首先从根节点 (7,2) 出发，将当前最近邻设为 (7,2)，对该 KDTree 作深度优先遍历。
2. 以 (3,5) 为圆心，其到 (7,2) 的距离为半径画圆（多维空间为超球面），可以看出 (8,1) 右侧的区域与该圆不相交，所以 (8,1) 的右子树全部忽略。
3. 接着走到 (7,2) 左子树根节点 (5,4)，与原最近邻对比距离后，更新当前最近邻为 (5,4)。
4. 以 (3,5) 为圆心，其到 (5,4) 的距离为半径画圆，发现 (7,2) 右侧的区域与该圆不相交，忽略改厕所有节点，这样 (7,2) 的整个右子树被标记为已忽略。
5. 遍历完 (5,4) 的左右叶子节点，发现与当前最优距离相等，不更新最近邻。所以 (3,5) 的最近邻为 (5,4)。

KDTree 的查询复杂度为O(kn(k−1)/k)，k 表示维度，n 表示数据量。说明 k 越大，复杂度越接近线性，所以它并不适合高维向量召回。

2.1.2 Annoy

Annoy是Erik Bernhardsson写的一个以树为作为索引结构的近似最近邻搜索库，并用在Spotify的推荐系统中。

Annoy的核心是不断用选取的两个质心的法平面对空间进行分割，最终将每一个划分的子空间里面的样本数据限制在K以内。对于待插入的样本xi，从根节点依次使用法向量跟xi做内积运算，从而判断使用法平面的哪一边（左子树or右子树）。对于查询向量qi，采用同样的方式（在树结构上体现为从根节点向叶子节点递归遍历），即可定位到跟qi在同一个子空间或者邻近的子空间的样本，这些样本即为qi近邻。

为了提高查询召回率，Annoy采用建立多棵子树的方式，这种方式其实有点类似AdaBoost的意思，即用多个弱分类器构成强单元分类器，NV-tree也采用了这种方式，哈希方法也同样采用了这种方式（构建多表）的方式。

值得注意的是，Annoy如果不保存原始特征，则Annoy只能返回查询的k个近邻，至于这k个里面的排序顺序是怎么样的，它是不知道的，如果需要知道，需要对这k个返回的结果，获取原始特征，再计算各自的相似度，排序一下即可得到这k个结果的排序。

2.2 基于Hash的方法

哈希就是将连续的一系列值映射到较短的离散值，在这里一般是指映射到0、1值。根据学习的策略，可以将哈希方法分为无监督、有监督和半监督三种类型。

2.2.1 LSH(Local Sensitive Hashing)

LSH的中文名称是局部敏感哈希算法，而哈希函数满意局部敏感的定义是在哈希后的空间内，相近的样本点对比相远的样本点更容易发生碰撞。个人理解就是会有一些聚类的效果。

LSH加速检索的原理
如下图所示，我们选取多个局部敏感hash函数，把候选集向量通过平面分割做 hash。0表示点在平面的左侧，1表示点在平面的右侧。由于应用了多个局部敏感hash函数，可以发现hash值相同的点都比较相近，也即查询样本的最近邻将极有可能落在查询样本的cell中。所以我们在检索的时候只需要计算hash值相似的向量就能够召回较为精确度的topK。

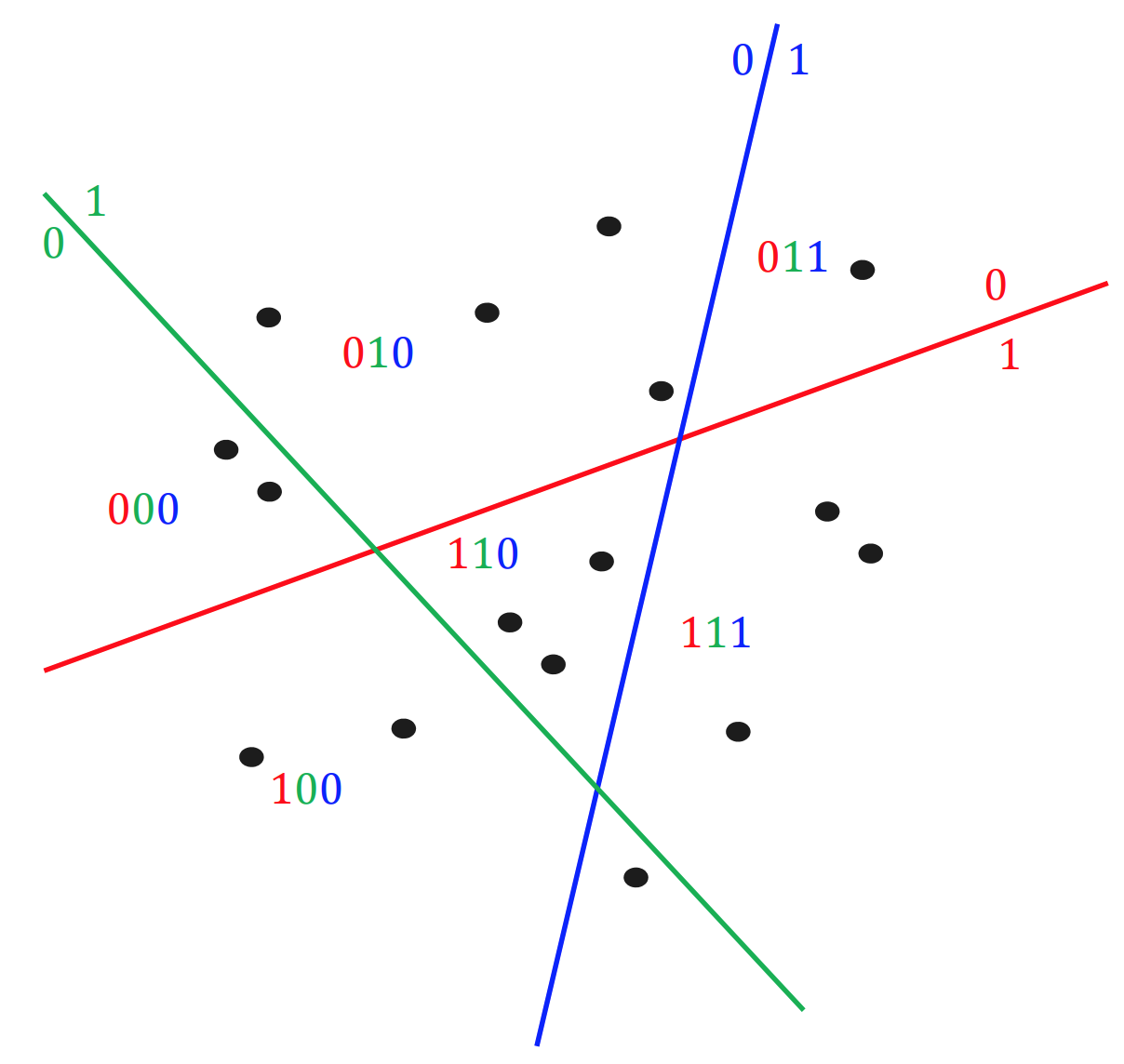
为什么要用多表哈希？
对于单表哈希，当哈希函数数目K（上图中是2）取得太大，查询样本与其对应的最近邻落入同一个桶中的可能性会变得很微弱，针对这个问题，我们可以重复这个过程L次，从而增加最近邻的召回率。这个重复L次的过程，可以转化为构建L（上图中是3）个哈希表，这样在给定查询样本时，我们可以找到L个哈希桶（每个表找到一个哈希桶），然后我们在这L个哈希表中进行遍历。这个过程相当于构建了K*L个哈希函数(注意是“相当”，不要做“等价”理解)。

多表哈希中哈希函数数目K和哈希表数目L如何选取？
哈希函数数目K如果设置得过小，会导致每一个哈希桶中容纳了太多的数据点，从而增加了查询响应的时间；
而当K设置得过大时，会使得落入每个哈希桶中的数据点变小，而为了增加召回率，我们需要增加L以便构建更多的哈希表，但是哈希表数目的增加会导致更多的内存消耗，并且也使得我们需要计算更多的哈希函数，同样会增加查询相应时间。
但是在K过大或过小之间仍然可以找到一个比较合理的折中位置。通过选取合理的K和L，我们可以获得比线性扫描极大的性能提升。

2.2.2 Multiprobe LSH

多probe LSH主要是为了提高查找准确率而引入的一种策略。
原始的LSH: 是对于构建的L个哈希表，我们在每一个哈希表中找到查询样本落入的哈希桶，然后再在这个哈希桶中做遍历.
而Multiprobe: 指的是我们不止在查询样本所在的哈希桶中遍历，还会找到其他的一些哈希桶，然后这些找到的T个哈希桶中进行遍历。
这些其他哈希桶的选取准则是：跟查询样本所在的哈希桶邻近的哈希桶，“邻近”指的是汉明距离度量下的邻近。

如果不使用Multiprobe，我们需要的哈希表数目L在100到1000之间，在处理大数据集的时候，其空间的消耗会非常的高，幸运地是，因为有了上面的Multiprobe的策略，LSH在任意一个哈希表中查找到最近邻的概率变得更高，从而使得我们能到减少哈希表的构建数目。

对于LSH，涉及到的主要的参数有三个：

• K，每一个哈希表的哈希函数（空间划分）数目
• L，哈希表（每一个哈希表有K个哈希函数）的数目
• T，近邻哈希桶的数目，即the number of probes

这三个设置参数可以按照如下顺序进行：

1. 首先，根据可使用的内存大小选取L，然后在K和T之间做出折中：哈希函数数目K越大，相应地，近邻哈希桶的数目的数目T也应该设置得比较大，反之K越小，L也可以相应的减小。
2. 获取K和L最优值的方式可以按照如下方式进行：对于每个固定的K，如果在查询样本集上获得了我们想要的精度，则此时T的值即为合理的值。
3. 在对T进行调参的时候，我们不需要重新构建哈希表，甚至我们还可以采用二分搜索的方式来加快T参数的选取过程。

LSH开源实现

关于LSH开源工具库，有很多，这里推荐两个LSH开源工具包：LSHash和FALCONN, 分别对应于学习和应用场景。

LSHash
LSHash非常适合用来学习，里面实现的是最经典的LSH方法，并且还是单表哈希。哈希函数的系数采用随机的方式生成，具体代码如下：

def _generate_uniform_planes(self):
    """ Generate uniformly distributed hyperplanes and return it as a 2D
    numpy array.
    """

    return np.random.randn(self.hash_size, self.input_dim)

hash_size为哈希函数的数目，即前面介绍的K。如果要在实用中使用LSH，可以使用FALCONN。

2.2.3 FALCONN

FALCONN是经过极致优化的LSH，其对应的论文为NIPS 2015 Practical and Optimal LSH for Angular Distance，Piotr Indyk系作者之一，下面将其Python例子中初始化索引以及构建哈希表的部分提取出来，对其中的参数做一下简要的分析.

# Hyperplane hashing
params_hp = falconn.LSHConstructionParameters()
params_hp.dimension = d
params_hp.lsh_family = 'hyperplane'
params_hp.distance_function = 'negative_inner_product'
params_hp.storage_hash_table = 'flat_hash_table'
params_hp.k = 19
params_hp.l = 10
params_hp.num_setup_threads = 0
params_hp.seed = seed ^ 833840234

print('Hyperplane hash\n')

start = timeit.default_timer()
hp_table = falconn.LSHIndex(params_hp)
hp_table.setup(data)
hp_table.set_num_probes(2464)

有3个很重要的参数，分别是k、l和set_num_probes，对应的具体意义即前面所述。

性能方面FALCONN的索引构建过程非常快，百万量级数据，维度如果是128维，其构建索引时间大概2-3min的样子，实时搜索可以做到几毫秒响应时间。

对于小数据集和中型规模的数据集(几个million-几十个million)， FALCONN和NMSLIB是一个非常不错的选择，如果对于大型规模数据集(几百个million以上)，基于矢量量化的Faiss是一个明智的选择。

遗留问题
FALCONN还不是很完善，比如对于数据的动态增删目前还不支持，NMSLIB目前也不支持。
一般而言，动态的增删在实际应用场合是一个基本的要求，但是我们应注意到，增删并不是毫无限制的，在增删频繁且持续了一段时间后，这时的数据分布已经不是我们原来建索引的数据分布形式了，我们应该重新构建索引。在这一点上，基于矢量量化的方法对数据的动态增删更友好。

在召回率上一般哈希向量量化方法比矢量量化方法要差一些。
一个比较直观的理解是：哈希向量量化后在计算距离的时候，计算的是汉明距离，在向量量化比特位长度相同的条件下，汉明距离表示的距离集合是有限的，而矢量量化计算的距离是一个实数，意味着它构成的距离集合是无限的。

所以，实际工业采用的向量索引方法，主要还是矢量量化方法居多，主要原因有二：

• 矢量量化方法能够较好的兼顾检索召回率以及量化压缩比；
• 增删友好的优点使得构建的服务更稳定；

2.3 矢量量化方法

矢量量化方法，Vector Quantization，定义为：将一个向量空间中的点用其中的一个有限子集来进行编码的过程。其关键是码本的建立和码字搜索算法。

2.3.1 多阶段矢量量化（MSVQ）

多阶段矢量量化（Multi-Stage Vector Quantization，MSVQ）也称为残差矢量量化（Residual Vector Quantization, RVQ）。它是一种思想，即将编码任务分解为一系列级联过程。级联过程可以用下图直观的展示出来：

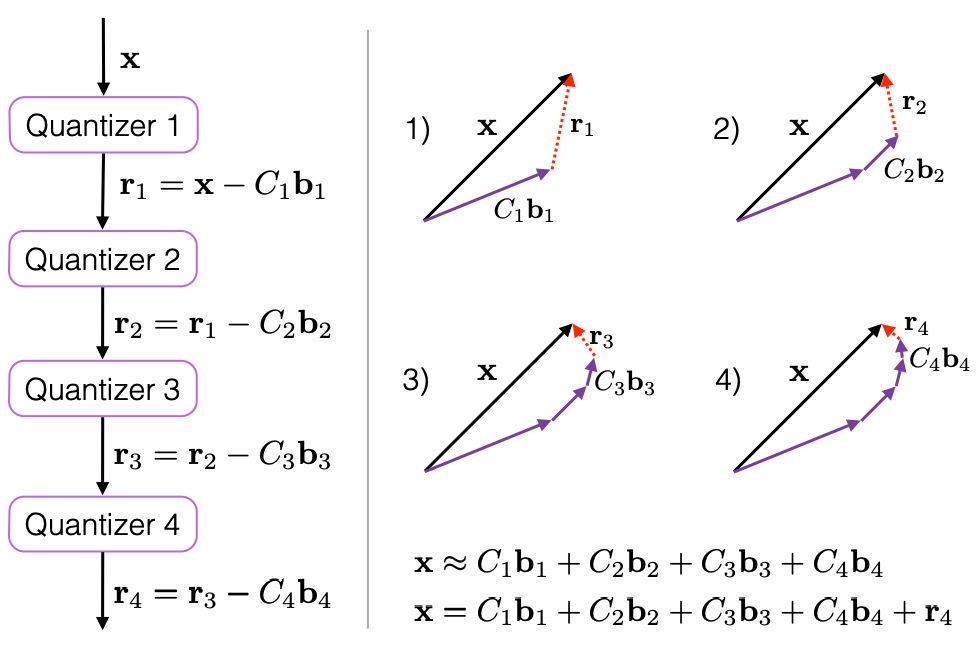
如上图所示，途中quantizer为量化器，可以认为就是码本生成器。对于待量化的向量x：

1. 经过一级量化器quantizer1后，得到的量化残差为r1 = x - C1b1；
2. 其中C1为一级量化器的码本，b1为x经过一级量化器quantizer1后的表示结果；
3. 将一级量化误差r1作为二级量化器的输入，后面过程与此类似。

通过这种级联量化的量化方式，当构建的量化器为无穷个时，x可以被这无穷个码本精确表示。上图右侧子图比较直观的描绘了x被多个码本逐步近似的过程。

码本的构建和查询
图中的C1、C2、…、Ci、… 这些码本在构建的时候，可以采用KMeans等方式得到各个量化器的码本。以上面构建的4个级联的码本为例，当得到码本C1、C2、C3、C4后，x量化的结果即可用[b1, b2, b3, b4]表示。对于xq查询向量与x距离的计算，在计算xq与 C1、C2、…、Ci、… 之间的内积距离表后，可以通过查表的方式，获取到非对称距离。

这种多阶段级联的矢量量化方式，相比单阶段一次性量化，极大的降低了码本在训练过程中消耗的计算资源。

举个例子，4个阶段的MSVQ，每阶段用KMeans只需构建构建256大小的码本，则对空间分割构建的cell数目为$256^4=4294967296$，效率是很高的，但是如果采用单阶段一次性量化构建4294967296大小的码本，这个码本根本没法用KMeans聚出来。
此外在计算距离的时候，采用4阶段的MSVQ方式，只需计算4x256次距离的计算构成距离表，然后采用查表方式计算距离，而单阶段一次性量化需要计算4294967296次的距离计算。MSVQ的进一步加速版本是倒排MSVQ，将一级码本视为倒排链，从而构建倒排结构，构建MSVQ倒排结构。我们可以将MSVQ类比成“深度加深”的过程

2.3.2 乘积量化(PQ)

乘积量化(Product Quantization，PQ)是Herve Jegou在2011年提出的一种非常经典实用的矢量量化索引方法，在工业界向量索引中已得到广泛的引用，并作为主要的向量索引方法，在Fasis有非常高效的实现。

乘积量化的核心思想:分段（划分子空间）和聚类，或者说具体应用到ANN近似最近邻搜索上，KMeans是PQ乘积量化子空间数目为1的特例。

PQ乘积量化生成码本和量化的过程可以用如下图示来说明：

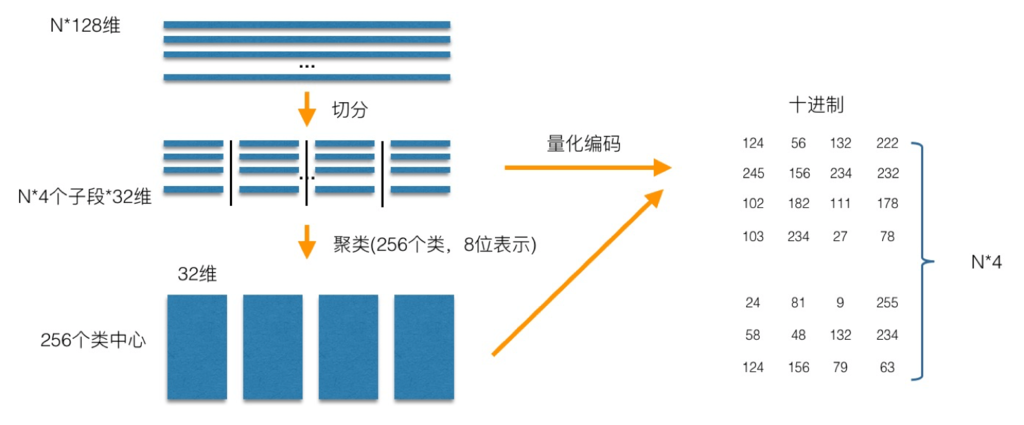
在训练阶段:

1. 针对N个训练样本，假设样本维度为128维，我们将其切分为4个子空间，则每一个子空间的维度为32维;
2. 然后我们在每一个子空间中，对子向量采用K-Means对其进行聚类(图中示意聚成256类)，这样每一个子空间都能得到一个码本。
3. 这样训练样本的每个子段，都可以用子空间的聚类中心来近似，对应的编码即为类中心的ID。
4. 如图所示，通过这样一种编码方式，训练样本仅使用的很短的一个编码得以表示，从而达到量化的目的。
5. 对于待编码的样本，将它进行相同的切分，然后在各个子空间里逐一找到距离它们最近的类中心，然后用类中心的id来表示它们，即完成了待编码样本的编码。

在查询阶段:

1. PQ同样在计算查询样本与dataset中各个样本的距离，只不过这种距离的计算转化为间接近似的方法而获得。
2. PQ乘积量化方法在计算距离的时候，有两种距离计算方式，一种是对称距离，另外一种是非对称距离。
3. 非对称距离的损失小(也就是更接近真实距离)，实际中也经常采用这种距离计算方式。

下面过程示意的是查询样本来到时，以非对称距离的方式(红框标识出来的部分)计算到dataset样本间的计算示意：

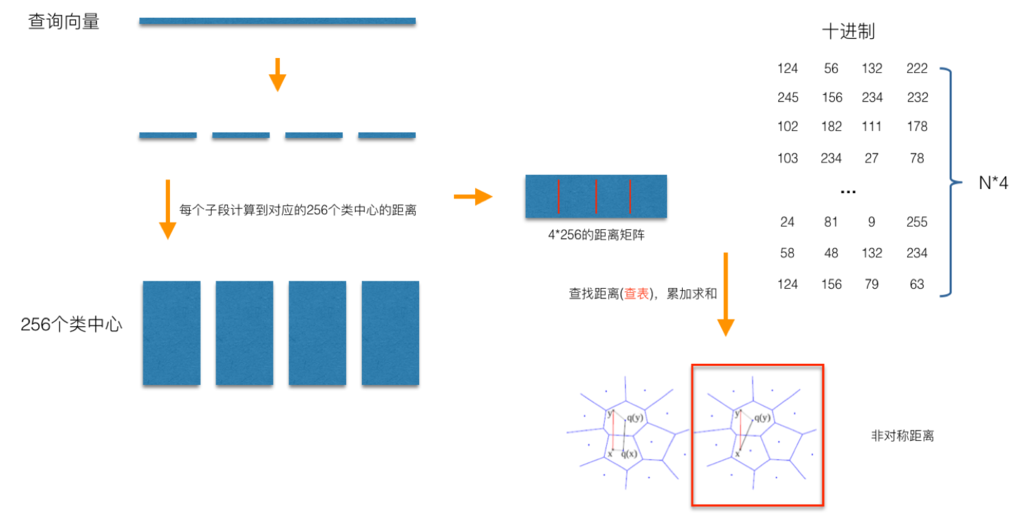
查询向量来到时:

1. 按训练样本生成码本的过程，将其同样分成相同的子段，然后在每个子空间中，计算子段到该子空间中所有聚类中心得距离。(如图中所示，可以得到4x256个距离，这里为便于后面的理解说明，可以把这些算好的距离称作距离表)。
2. 在计算库中某个样本到查询向量的距离时，比如编码为(124, 56, 132, 222)这个样本到查询向量的距离时，我们分别到距离表中取各个子段对应的距离即可。(比如编码为124这个子段，在第1个算出的256个距离里面把编号为124的那个距离取出来就可)。
3. 所有子段对应的距离取出来后，将这些子段的距离求和相加，即得到该样本到查询样本间的非对称距离。
4. 所有距离算好后，排序后即得到我们最终想要的结果。

PQ乘积量化能够加速索引的原理：
即将全样本的距离计算，转化为到子空间类中心的距离计算。

• 比如上面所举的例子，原本brute-force search的方式计算距离的次数随样本数目N成线性增长，但是经过PQ编码后，对于耗时的距离计算，只要计算4x256次，几乎可以忽略此时间的消耗。
• 另外，从上图也可以看出，对特征进行编码后，可以用一个相对比较短的编码来表示样本，自然对于内存的消耗要大大小于brute-force search的方式。

在某些特殊的场合，我们总是希望获得精确的距离，而不是近似的距离，并且我们总是喜欢获取向量间的余弦相似度（余弦相似度距离范围在[-1,1]之间，便于设置固定的阈值），针对这种场景，可以针对PQ乘积量化得到的前top@K做一个brute-force search的排序。

2.3.3 倒排乘积量化（IVFPQ）

倒排PQ乘积量化(IVFPQ)是PQ乘积量化的更进一步加速版。其加速的本质依然是加速原理：为了加快查找的速度，几乎所有的ANN方法都是通过对全空间分割，将其分割成很多小的子空间，在搜索的时候，通过某种方式，快速锁定在某一（几）子空间，然后在该（几个）子空间里做遍历。

仔细观察PQ乘积量化存在一定的优化空间：
其在计算距离的时候，虽然已经预先算好了，但是对于每个样本到查询样本的距离，还是得老老实实挨个去求和相加计算距离。
实际上我们感兴趣的是那些跟查询样本相近的样本（姑且称这样的区域为感兴趣区域），也就是说老老实实挨个相加其实做了很多的无用功。如果能够通过某种手段快速将全局遍历锁定为感兴趣区域，则可以舍去不必要的全局计算以及排序。
倒排PQ乘积量化的”倒排“，正是这样一种思想的体现，在具体实施手段上，采用的是通过聚类的方式实现感兴趣区域的快速定位，在倒排PQ乘积量化中，聚类可以说应用得淋漓尽致。

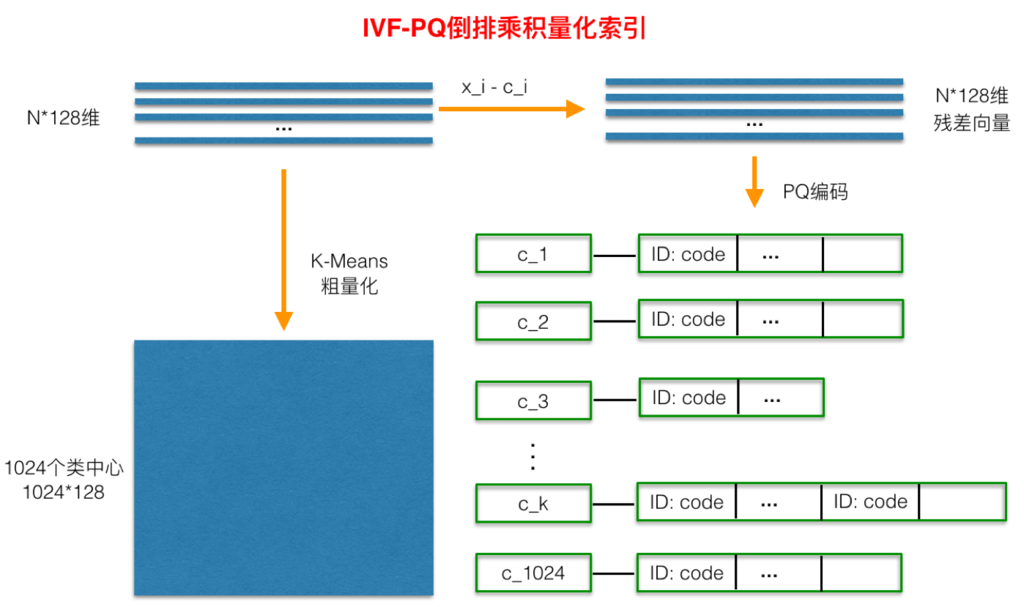
如上图所示：在PQ乘积量化之前，增加了一个粗量化过程。

具体地:

1. 先对N个训练样本采用KMeans进行聚类，这里聚类的数目一般设置得不应过大，一般设置为1024差不多，这种可以以比较快的速度完成聚类过程。
2. 得到了聚类中心后，针对每一个样本x_i，找到其距离最近的类中心c_i后，两者相减得到样本x_i的残差向量(x_i-c_i);
3. 后面剩下的过程，就是针对(x_i-c_i)的PQ乘积量化过程。

在查询的时候，通过相同的粗量化，可以快速定位到查询向量属于哪个c_i（即在哪一个感兴趣区域），然后在该感兴趣区域按上面所述的PQ乘积量化距离计算方式计算距离。

2.3.4 最优乘积量化（OPQ）

最优乘积量化（Optimal Product Quantization, OPQ）是PQ的一种改进版本。其改进体现在，致力于在子空间分割时，对各子空间的方差进行均衡。

Optimal的过程一般实现为一个组件。而用于检索的原始特征维度较高，所以实际在使用PQ等方法构建索引的时候，常会对高维的特征使用PCA等降维方法对特征先做降维处理。

这样降维预处理，可以达到两个目的：

• 一是降低特征维度；
• 二是在对向量进行子段切分的时候要求特征各个维度是不相关的，做完PCA之后，可以一定程度缓解这个问题。

但是这么做了后，在切分子段的时候，采用顺序切分子段仍然存在一定的问题，这个问题可以借用ITQ中的一个二维平面的例子加以说明：

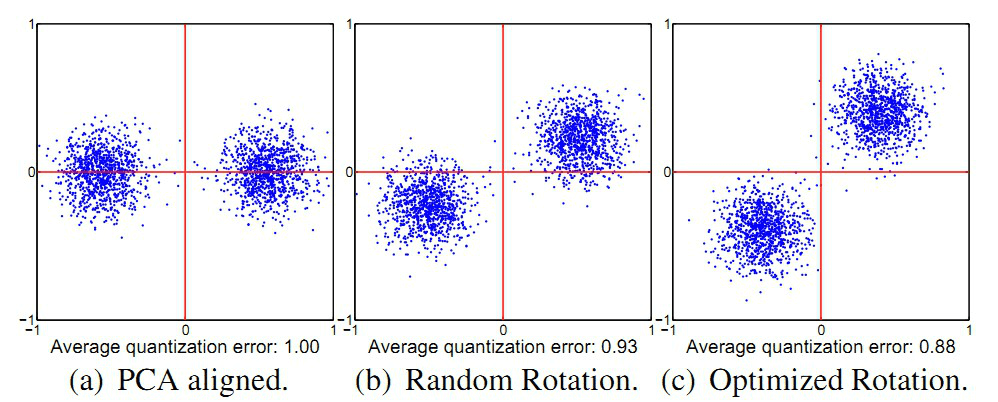
这个问题就是：
如上面a图所示，对于PCA降维后的二维空间，假设在做PQ的时候，将子段数目设置为2段，即切分成x和y两个子向量，然后分别在x和y上做聚类（假设聚类中心设置为2）。
对a图和c图聚类的结果进行比较，可以明显的发现，a图在y方向上聚类的效果明显差于c图，而PQ又是采用聚类中心来近似原始向量（这里指降维后的向量），也就是c图是我们需要的结果。

这个问题可以转化为数据方差来描述：在做PQ编码时，对于切分的各个子空间，我们应尽可能使得各个子空间的方差比较接近，最理想的情况是各个子空间的方差都相等。

解决办法：
为了在切分子段的时候，使得各个子空间的方差尽可能的一致，Herve Jegou在Aggregating local descriptors into a compact image representation中提出使用一个正交矩阵来对PCA降维后的数据再做一次变换，使得各个子空间的方差尽可能的一致。

OPQ致力于解决的问题正是对各个子空间方差的均衡。思想主要是在聚类的时候对聚类中心寻找对应的最优旋转矩阵，使得所有子空间中各个数据点到对应子空间的类中心的L2损失的求和最小。

OPQ在具体求解的时候，分为非参求解方法和带参求解方法，具体为：

• 非参求解方法。跟ITQ的求解过程一样。
• 带参求解方法。带参求解方法假设数据服从高斯分布，在此条件下，最终可以将求解过程简化为数据经过PCA分解后，特征值如何分组的问题。在实际中，该解法更具备高实用性。

2.4 基于图索引量化方法

图索引量化是一种将图引入向量索引的方法，由于图索引的高召回特点，近几年基于图索引量化方法出现了不少这方面的工作，比如早期的KNNGraph和最近的将基于图索引量化方法推向成熟应用的HNSW方法。

首先从检索的召回率上来评估，基于图的索引方法要优于目前其他一些主流ANN搜索方法，比如乘积量化方法（PQ、OPQ）、哈希方法等。虽然乘积量化方法的召回率不如HNSW，但由于乘积量化方法具备内存耗用更小、数据动态增删更灵活等特性，使得在工业检索系统中，在对召回率要求不是特别高的场景下，乘积量化方法在工业界，仍然是使用得较多的一种索引方法。

下面是乘积量化和图索引方法特性做的一个对比，以HNSW和OPQ为典型代表：

特性	OPQ	HNSW
内存占用	小	大
召回率	较高	高
数据动态增删	灵活	不易

基于图索引的ANN方法由于数据在插入索引的时候，需要计算（部分）数据间的近邻关系，因而需要实时获取到到数据的原始特征，几乎所有基于图ANN的方法在处理该问题的时候，都是直接将原始特征加载在内存（索引）里，从而造成对内存使用过大，至于召回率图ANN方法要比基于量化的方法要高，这个理解起来比较直观。

2.4.1 NSW

在介绍经典的HNSW之前我们先介绍它的前身NSW，该算法如下图，它是一个顺序构建图流程：

我们以图中第5次构造D点为例来介绍流程：

1. 构建的时候，我们约定每次加入节点只连 3 条边，防止图变大，在实际使用中，要通过自身的数据；
2. 随机一个节点，比如 A，保存下与 A 的距离，然后沿着 A 的边遍历，E 点最近，连边。然后再重新寻找，不能与之前重复，直到添加完 3 条边；

查找流程包含在了插入流程中，一样的方式，只是不需要构建边，直接返回结果。

2.4.2 HNSW

Hierarchical Navigable Small World Graphs (HNSW) 是Yury A. Malkov提出的一种基于图索引的方法，它是Yury A. Malkov在他本人之前工作NSW上一种改进。通过采用层状结构，将边按特征半径进行分层，使每个顶点在所有层中平均度数变为常数，从而将NSW的计算复杂度由多重对数(Polylogarithmic)复杂度降到了对数(logarithmic)复杂度。

HNSW的主要贡献如下：

• 图输入节点明确的选择；
• 使用不同尺度划分链接；
• 使用启发式方式来选择最近邻；

近邻图技术

对于给定的近邻图，在开始搜索的时候，从若干输入点（随机选取或分割算法）开始迭代遍历整个近邻图。

在每一次横向迭代的时候，算法会检查链接或当前base节点之间的距离，然后选择下一个base节点作为相邻节点，使得能最好的最小化连接间的距离。

近邻图主要的缺陷：

1. 在路由阶段，如果随机从一个或者固定的阶段开始，迭代的步数会随着库的大小增长呈现幂次增加；
2. 当使用k-NN图的时候，一个全局连接可能的损失会导致很差的搜索结果。

算法描述

网络图以连续插入的方式构建。对于每一个要插入的元素，采用指数衰变概率分布函数来随机选取整数最大层。HNSW 算法是 NSW 算法的分层优化，借鉴了 skiplist 算法的思想，提升查询性能，开始先从稀疏的图上查找，逐渐深入到底层的图。

• 图构建元素插入过程（Algorithm 1）：从顶层开始贪心遍历graph，以便在某层A中找到最近邻。当在A层找到局部最小值之后，再将A层中找到的最近邻作为输入点（entry point），继续在下一层中寻找最近邻，重复该过程；
• 层内最近邻查找（Algorithm 2）：贪心搜索的改进版本；
• 搜索阶段，维护一个动态列表，用于保持ef个找到的最近邻元素

在搜索的初步阶段，ef参数设置为1。搜索过程包括zoom out和zoom in两个阶段，zoom out是远程路由，zoom in顾名思义就是在定位的区域做精细的搜索过程。
整个过程可以类比在地图上寻找某个位置的过程：

1. 我们可以地球当做最顶层，五大洲作为第二层，国家作为第三层，省份作为第四层……;
2. 现在如果要找海淀五道口，我们可以通过顶层以逐步递减的特性半径对其进行路由（第一层地球->第二层亚洲—>第三层中国->第四层北京->海淀区）;
3. 到了第0层后，再在局部区域做更精细的搜索。

参数详细意义

1. M：参数M定义了第0层以及其他层近邻数目，不过实际在处理的时候，第0层设置的近邻数目是2xM。如果要更改第0层以及其他层层近邻数目，在HNSW的源码中进行更改即可。另外需要注意的是，第0层包含了所有的数据点，其他层数据数目由参数mult定义，详细的细节可以参考HNSW论文。
2. delaunay_type：检索速度和索引速度可以通过该参数来均衡heuristic。HNSW默认delaunay_type为1，将delaunay_type设置为1可以提高更高的召回率(> 80%)，但同时会使得索引时间变长。因此，对于召回率要求不高的场景，推荐将delaunay_type设置为0。
3. post：post定义了在构建图的时候，对数据所做预处理的数量（以及类型），默认参数设置为0，表示不对数据做预处理，该参数可以设置为1和2（2表示会做更多的后处理）。

更详细的参数说明，可以参考parameters说明。

2.4.3 NSG算法

NSG 全写为 Navigating Spreading-out Graph。NSG 围绕四个方向来改进：

• 图的连通性;
• 减少出度;
• 缩短搜索路径;
• 缩减图的大小。

具体是通过建立导航点 (Navigation Point)，特殊的选边策略, 深度遍历收回离散节点（Deep Traversal）等方法。

首先是 Navigation Point，在建图时，首先需要一张预先建立的 K-nearest-neighbor-graph (KNNG) 作为构图基准。随机选择一个点作为 Navigation Point，后续所有新插入的节点在选边时都会将 Navigation Point 加入候选。在建图过程中，逐渐会将子图都和 Navigation point 相连接，这样其他的节点只需保持很少的边即可，从而减少了图的大小。每次搜索从 Navigation Point 出发能够指向具体的子图，从而减少无效搜索，获得更好搜索性能。

NSG 使用的择边策略与 HNSW 类似，但是不同于 HNSW 只选择最短边为有效边，NSG 使用的择边策略如下图。

• 以点 r 为例，当 r 与 p 建立连接时，以 r 和 p 为圆心，r 和 p 的距离为半径，分别做圆，如果两个圆的交集内没有其他与 p 相连接的点，则 r 与 p 相连（见图 3-B）。
• 在连接点 s 时，由于以 s 和 p 距离为半径的交集圆内，已有点 r 与 p 相连，所以 s 和 p 不相连（见图 3-C）。下图中最终与点 p 相连的点只有 r, t 和 q（见图 3-A）。

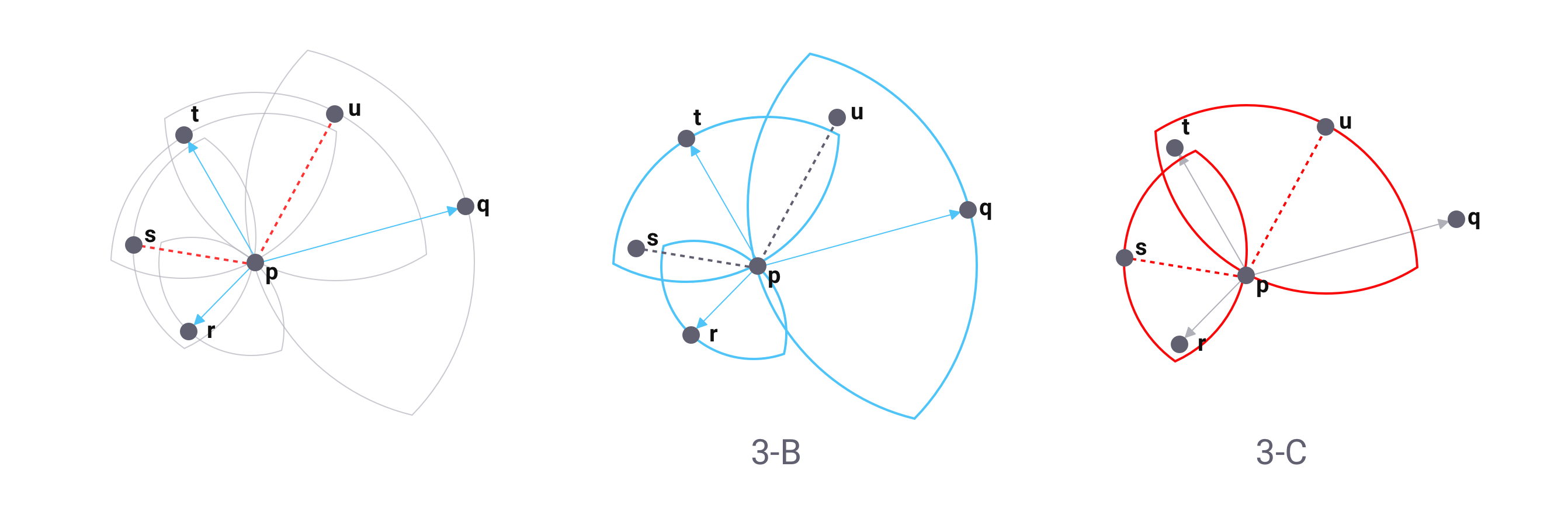
NSG 这样做的原因是考虑到由于边数一多，整个图就会变得稠密，最后在搜索时会浪费大量算力。但是减少边的数量，带来的坏处也比较明显，最后的图会是一张稀疏图，会使得有些节点难以被搜索到。不仅如此，NSG 的边还是单向边。在如此激进的策略下，图的连通性就会产生问题，这时 NSG 选择使用深度遍历来将离群的节点收回到图中。通过以上步骤，图的建立就完成了。

HNSW 和 NSG 的比较

HNSW 从结构入手，利用分层图提高图的导航性减少无效计算从而降低搜索时间，达到优化的目的。

而 NSG 选择将图的整体度数控制在尽可能小的情况下，提高导航性，缩短搜索路径来提高搜索效率。

下面我们从内存占用，搜索速度，精度等方面来比较 HNSW 和 NSG。

1. HNSW 由于多层图的结构以及连边策略，导致搜索时内存占用量会大于 NSG，在内存受限场景下选择 NSG 会更好。
2. 但是 NSG 在建图过程中无论内存占用还是耗时都大于 HNSW。此外 HNSW 还拥有目前 NSG 不支持的特性，即增量索引，虽然耗时巨大。
3. 对比其他的索引类型，无论 NSG 还是 HNSW 在搜索时间和精度两个方面，都有巨大优势。

目前在 Milvus 内部已经实现了 NSG 算法，并将 KNNG 计算放到了 GPU 上进行从而极大地加快了 NSG 图的构建。

3 算法总结

KNN 适合场景：

• 数据量小(单分片100w以下)；
• 先过滤其他条件，只剩少量数据，再向量召回的场景；
• 召回率100%；

ANN 场景：

• 数据量大(千万级以上)；
• 先向量过滤再其他过滤；
• 召回率不需要100%；
• LSH 算法： 召回率性能要求不高，少量增删；
• IVFPQ 算法：召回率性能要求高，数据量大(千万级)，少量增删，需要提前构建；
• HNSW 算法： 召回率性能要求搞，数据量适中(千万以下)，索引全存内存，内存够用；

参考文章
蚂蚁金服 ZSearch 在向量检索上的探索
大规模特征向量检索算法总结 (LSH PQ HNSW)
图像检索：向量索引
Milvus 揭秘系列（一）：向量索引算法 HNSW 和 NSG 的比较