推荐系统三十六式--学习笔记（17-19 MAB问题）

17.【MAB问题】简单却有效的Bandit算法

MAB 问题

Bandit 算法来源于人民群众喜闻乐见的赌博学，它要解决的问题是这样的。

一个赌徒，要去摇老虎机，走进赌场一看，一排老虎机，外表一模一样，但是每个老虎机吐钱的概率可不一样，他不知道每个老虎机吐钱的概率分布是什么，那么想最大化收益该怎么整？

这就是多臂赌博机问题 (Multi-armed bandit problem, K-armed bandit problem, MAB)，简称 MAB 问题。有很多相似问题都属于 MAB 问题。

假设一个用户对不同类别的内容感兴趣程度不同，当推荐系统初次见到这个用户时，怎么快速地知道他对每类内容的感兴趣程度？这也是推荐系统常常面对的冷启动问题。

假设系统中有若干广告库存物料，该给每个用户展示哪个广告，才能获得最大的点击收益，是不是每次都挑收益最好那个呢？

算法工程师又设计出了新的策略或者模型，如何既能知道它和旧模型相比谁更靠谱又对风险可控呢？

推荐系统里面有两个顽疾，一个是冷启动，一个是探索利用问题，后者又称为 EE 问题：Exploit－Explore 问题。针对这两个顽疾，Bandit 算法可以入药。

Bandit 算法

Bandit 算法并不是指一个算法，而是一类算法。首先，来定义一下，如何衡量选择的好坏？Bandit 算法的思想是：看看选择会带来多少遗憾，遗憾越少越好。在 MAB 问题里，用来量化选择好坏的指标就是累计遗憾，计算公式如下所示。

$\begin{align} R_T &= \sum_{i=1}^T(w_{opt}-w_{B(i)})\\ &= Tw^*-\sum_{i=1}^Tw_{B(i)} \end{align}$

公式有两部分构成：一个是遗憾，一个是累积。求和符号内部就表示每次选择的遗憾多少。

$W_{opt}$ 就表示，每次都运气好，选择了最好的选择，该得到多少收益，WBi 就表示每一次实际选择得到的收益，两者之差就是“遗憾”的量化，在 T 次选择后，就有了累积遗憾。

在这个公式中：为了简化 MAB 问题，每个臂的收益不是 0，就是 1，也就是伯努利收益。这个公式可以用来对比不同 Bandit 算法的效果：对同样的多臂问题，用不同的 Bandit 算法模拟试验相同次数，比比看哪个 Bandit 算法的累积遗憾增长得慢，那就是效果较好的算法。

Bandit 算法的套路就是：小心翼翼地试，越确定某个选择好，就多选择它，越确定某个选择差，就越来越少选择它。

如果某个选择实验次数较少，导致不确定好坏，那么就多给一些被选择机会，直到确定了它是金子还是石头。简单说就是，把选择的机会给“确定好的”和“还不确定的”。

Bandit 算法中有几个关键元素：臂，回报，环境。

臂：是每次选择的候选项，好比就是老虎机，有几个选项就有几个臂；

回报：就是选择一个臂之后得到的奖励，好比选择一个老虎机之后吐出来的金币；

环境：就是决定每个臂不同的那些因素，统称为环境。

将这个几个关键元素对应到推荐系统中来。

臂：每次推荐要选择候选池，可能是具体物品，也可能是推荐策略，也可能是物品类别；

回报：用户是否对推荐结果喜欢，喜欢了就是正面的回报，没有买账就是负面回报或者零回报；

环境：推荐系统面临的这个用户就是不可捉摸的环境。

1. 汤普森采样算法

原理：假设每个臂是否产生收益，起决定作用的是背后有一个概率分布，产生收益的概率为 p。每个臂背后绑定了一个概率分布；每次做选择时，让每个臂的概率分布各自独立产生一个随机数，按照这个随机数排序，输出产生最大随机数那个臂对应的物品。

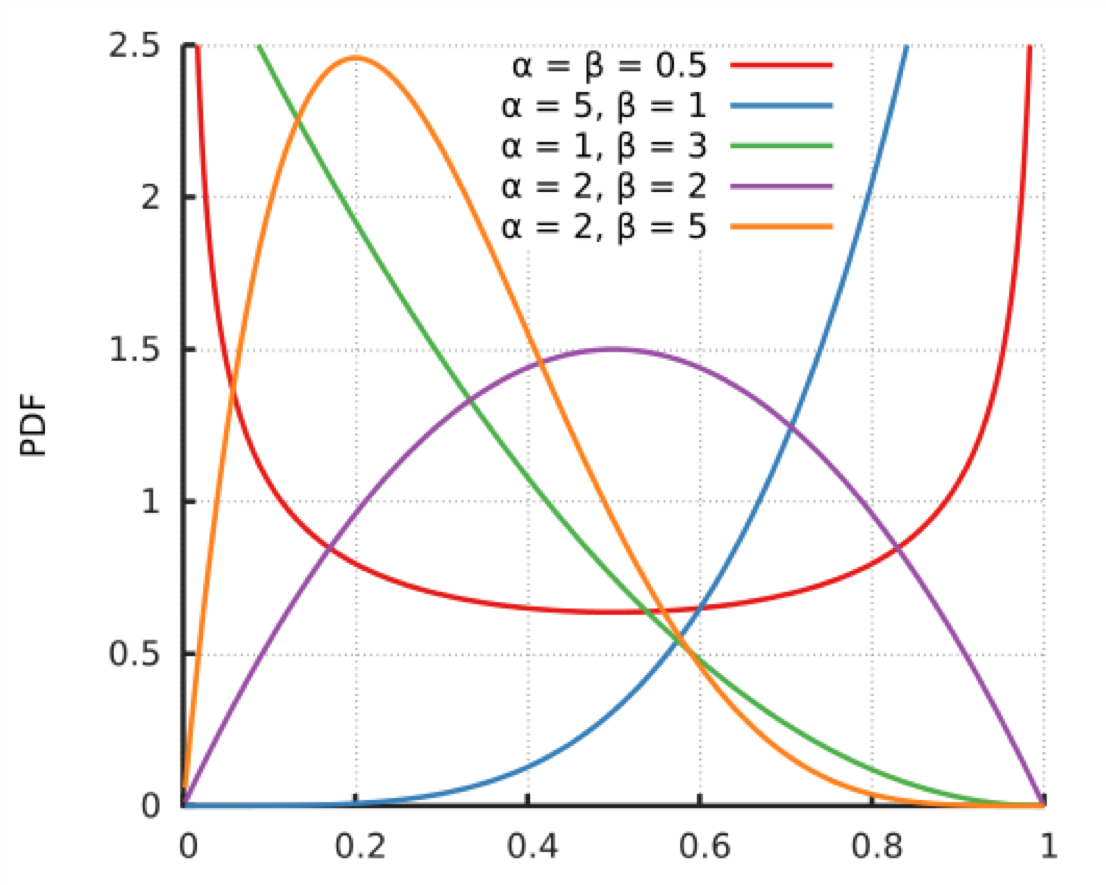
假设每个臂背后的概率分布是上图所示的beta分布，a 和 b 两个参数决定了分布的形状和位置：

当 a+b 值越大，分布曲线就越窄，分布就越集中，这样的结果就是产生的随机数会容易靠近中心位置；
当 a/(a+b) 的值越大，分布的中心位置越靠近 1，反之就越靠近 0，这样产生的随机数也相应第更容易靠近 1 或者 0。

贝塔分布的这两个特点，可以把它分成三种情况：

曲线很窄，而且靠近 1；

曲线很窄，而且靠近 0；

曲线很宽。

把贝塔分布的 a 参数看成是推荐后得到用户点击的次数，把分布的 b 参数看成是没有得到用户点击的次数。按照这个对应，再来叙述一下汤普森采样的过程。

取出每一个候选对应的参数 a 和 b；
为每个候选用 a 和 b 作为参数，用贝塔分布产生一个随机数；
按照随机数排序，输出最大值对应的候选；
观察用户反馈，如果用户点击则将对应候选的 a 加 1，否则 b 加 1；
注意，实际上在推荐系统中，要为每一个用户都保存一套参数，比如候选有 m 个，用户有 n 个，那么就要保存 2mn 个参数。

有效性的原因：

如果一个候选被选中的次数很多，也就是 a+b 很大了，它的分布会很窄，换句话说这个候选的收益已经非常确定了，用它产生随机数，基本上就在中心位置附近，接近平均收益。

如果一个候选不但 a+b 很大，即分布很窄，而且 a/(a+b) 也很大，接近 1，那就确定这是个好的候选项，平均收益很好，每次选择很占优势，就进入利用阶段，反之则几乎再无出头之日。

如果一个候选的 a+b 很小，分布很宽，也就是没有被选择太多次，说明这个候选是好是坏还不太确定，那么用它产生随机数就有可能得到一个较大的随机数，在排序时被优先输出，这就起到了前面说的探索作用。

用 Python 实现汤普森采样就一行：

1
2
3

import numpy
import pymc
choice = numpy.argmax(pymc.rbeta(1 + self.wins, 1 + self.trials - self.wins))

2.UCB 算法

第二个常用的 Bandit 算法就是 UCB 算法，UCB 算法全称是 Upper Confidence Bound，即置信区间上界。它也为每个臂评分，每次选择评分最高的候选臂输出，每次输出后观察用户反馈，回来更新候选臂的参数。每个臂的评分公式为:

$\bar x_j(t)+\sqrt{\frac{2ln t}{T_{j,t}}}$

公式有两部分，加号前面是这个候选臂到目前的平均收益，反应了它的效果，后面的叫做 Bonus，本质上是均值的标准差，反应了候选臂效果的不确定性，就是置信区间的上边界。t 是目前的总选择次数，$T_{jt}$ 是每个臂被选择次数。

思想：

以每个候选的平均收益为基准线进行选择；
对于被选择次数不足的给予照顾；
选择倾向的是那些确定收益较好的候选。

3. Epsilon 贪婪算法

朴素的一个算法，简单有效，类似于模拟退火。具体步骤：

先选一个 (0,1) 之间较小的数，叫做 Epsilon，也是这个算法名字来历。
每次以概率 Epsilon 做一件事：所有候选臂中随机选一个，以 1-Epsilon 的概率去选择平均收益最大的那个臂。
Epsilon 的值可以控制对探索和利用的权衡程度。这个值越接近 0，在探索上就越保守。
相似的，还有一个更朴素的做法：先试几次，等每个臂都统计到收益之后，就一直选均值最大那个臂。

4. 效果对比

对于上述算法，可以用仿真的方法对比效果，结果如下图：

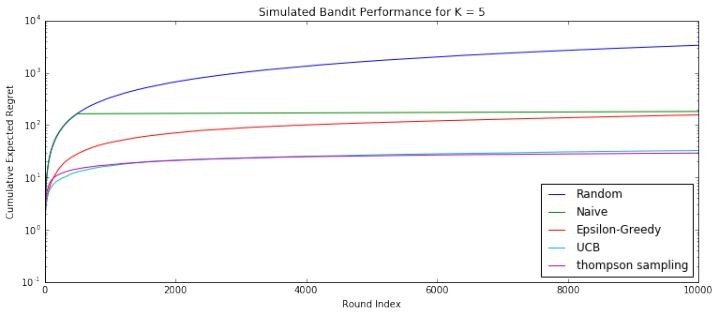
Bandit效果对比图.jpg

从上到下分别是下面几种。

完全随机：就是不顾用户反馈的做法。

朴素选择：就是认准一个效果好的，一直推。

Epsilon 贪婪算法：每次以小概率尝试新的，大概率选择效果好的。

UCB：每次都会给予机会较少的候选一些倾向。

汤普森采样：用贝塔分布管理每一个候选的效果。
UCB 算法和汤普森采样都显著优秀很多。

冷启动

推荐系统冷启动问题可以用 Bandit 算法来解决一部分。
大致思路如下：

用分类或者 Topic 来表示每个用户兴趣，我们可以通过几次试验，来刻画出新用户心目中对每个 Topic 的感兴趣概率。
这里，如果用户对某个 Topic 感兴趣，就表示我们得到了收益，如果推给了它不感兴趣的 Topic，推荐系统就表示很遗憾 (regret) 了。
当一个新用户来了，针对这个用户，我们用汤普森采样为每一个 Topic 采样一个随机数，排序后，输出采样值 Top N 的推荐 Item。注意，这里一次选择了 Top N 个候选臂。
等着获取用户的反馈，没有反馈则更新对应 Topic 的 b 值，点击了则更新对应 Topic 的 a 值。

三种算法的不足

1. Epsilon贪婪算法的不足

(1) Epsilon贪婪算法中的概率值(Epsilon值)定多少是合理的，能由候选集的条件判断比较合理的范围吗？这个值需要做试验和根据算法结果调整吗？
(2) 如果p值是固定的，总有一部分用户是肯定要看到不好的结果的，随着算法搜集到更多的反馈不会改善这个效果。
(3) 如果有大量的劣质资源，即使平均收益最大的臂可能都比整个候选集中最好的臂的收益差很多。Exploration的过程中会导致用户对整个系统丧失耐心，好的坏的都不愿意反馈。这样Exploit到好的候选的几率就更低，时间更长，需要更多的用户来做试验。
(4) 如何在实际环境中衡量Epsilon贪婪算法对整体的贡献，怎么知道多少次点击或多少用户之后的临界值来判断这个算法是对整体起足够多的正面作用的？

2. UCB算法的不足

候选多时，很多候选都没有显示过，平均收益和其标准差会相同。这时候如何排序？如果纯粹随机，就可能需要较长时间得到候选集中更好的结果。UCB算法本质上是“确定性”（Det erministic）算法，随机探索的能力受到一定限制。

3. 汤普森采样的不足

汤普森采样相对已经比较好了，我自己想不出更好的解决办法。当有相当数量的候选点击率和点击次数都很接近时，系统Explore到好的候选需要一些资源 (时间，用户等)。回到上面Epsilon贪婪算法的不足中的(3)。如果开始时有大量的劣质资源，没有人工干预发现好的候选比较耗时，整个系统可能还未来得及给用户推荐好的候选已经进入负循环。

Epsilon贪婪算法的不足的(3)和(4)适用于所有的Bandit算法。

18.【MAB问题】结合上下文信息的Bandit算法

UCB 回顾

这些 Bandit 算法，都有一个特点：完全没有使用候选臂的特征信息。特征可是机器学习的核心要素，也是机器学习泛化推广的依赖要素。UCB 就是置信上边界的简称，所以 UCB 这个名字就反映了它的全部思想。置信区间可以简单直观地理解为不确定性的程度，区间越宽，越不确定，反之就很确定。

每个候选的回报均值都有个置信区间，随着试验次数增加，置信区间会变窄，相当于逐渐确定了到底回报丰厚还是可怜。

每次选择前，都根据已经试验的结果重新估计每个候选的均值及置信区间。

选择置信区间上界最大的那个候选。

选择置信区间上界最大的那个候选”，这句话反映了几个意思：

如果候选的收益置信区间很宽，相当于被选次数很少，还不确定，那么它会倾向于被多次选择，这个是算法冒风险的部分；
如果候选的置信区间很窄，相当于被选次数很多，比较确定其好坏了，那么均值大的倾向于被多次选择，这个是算法保守稳妥的部分；
UCB 是一种乐观冒险的算法，它每次选择前根据置信区间上界排序，反之如果是悲观保守的做法，可以选择置信区间下界排序。

LinUCB

“Yahoo!”的科学家们在 2010 年基于 UCB 提出了 LinUCB 算法，它和传统的 UCB 算法相比，最大的改进就是加入了特征信息，每次估算每个候选的置信区间，不再仅仅是根据实验，而是根据特征信息来估算，这一点就非常的“机器学习”了。

LinUCB 算法做了一个假设：一个物品被选择后推送给一个用户，其收益和特征之间呈线性关系。其简单版本就是让每一个候选臂之间完全互相无关，参数不共享。高级版本就是候选臂之间共享一部分参数。

简单版本

假设此时有一个特征—性别，四个产品需要推荐给用户。

用户	性别	特征
u1	男	$x_1$=[1,0]
u2	女	$x_2$=[0,1]

两个特征就是Bandit算法要面对的上下文，表示成特征就是下面的样子:

参数	候选品（商品）
$\theta_1$=[0.1,0.5]	华歌尔内衣
$\theta_2$=[0.2,0.6]	香奈儿口红
$\theta_3$=[0.9,0.1]	吉利剃须刀
$\theta_4$=[0.5,0.6]	苹果笔记本

每一次推荐时，用特征和每一个候选臂的参数去预估它的预期收益和置信区间。

$x_i \times \theta_j$，这就是给男性用户推荐剃须刀，给女性用户推荐口红，即使是新用户，也可以作出比随机猜测好的推荐，再观察用户是否会点击，用点击信息去更新那个被推荐了的候选臂的参数。
这里的例子简化了没有计算置信区间，这是 UCB 的精髓。下面补上。

假如 D 是候选臂是候选臂在 m 次被选择中积累的特征，相当于就是 m 条样本，特征维度是 d，所以 D 是一个矩阵，维度是 m x d。这 m 次被选择，每次得到用户的点击或者没点击，把这个反馈信息记录为一个 m x 1 的向量，叫做 C。所以这个候选臂对应的参数就是 d x 1 的向量，d 就是特征维度数，记录$\hat \theta$。
按照 LinUCB 认为，参数和特征之间线性相乘就应该得到收益：

$D_{m\times d} \times \hat \theta_{d \times 1} = C_{m \times 1}$

于是(这里D无法直接求逆的，所以下面会进行变换)： $\hat \theta_{d \times 1} = (D_{m \times d}^T)^{-1} C_{m \times 1}$
由于数据稀疏，实际上求参数西塔时是采用岭回归的方法，给原始特征矩阵加上一个单位对角矩阵后再参与计算：

$\hat \theta_{d \times 1} = (D_{m \times d}^T D_{m \times d} + I_{d \times d}) ^{-1} D_{m \times d}^T C_{m \times 1}$

每一个候选臂都像这样去更新它的参数，同时，得到参数后，在真正做选择时，用面对上下文的特征和候选臂的参数一起。除了估算期望收益，还要计算置信区间的上边界，如果 x 是上下文特征，则期望收益和置信上边界的计算方法分别是下面的样子。期望收益：

$\hat r = x_{d \times 1}^T \hat \theta_{d \times 1}$

置信区间上边界：

$\hat b = \alpha \sqrt{x_{d \times 1}^T(D_{m \times d}^T D_{m \times d} + I_{d \times d}) ^{-1} x_{d \times 1}}$

这两个计算结果都是标量数值。置信区间计算公式虽然看起来复杂，实际上反应的思想也很直观，随着被选择次数的增加，也就是 m 增加，这个置信上边界是越来越小的。每一次选择时给每一个候选臂都计算这两个值，相加之后选择最大那个候选臂输出，就是 LinUCB 了。
岭回归（ridge regression）主要用于当样本数小于特征数时，对回归参数进行修正。对于加了特征的 Bandit 问题，正好符合这个特点：试验次数（样本）少于特征数。

LinUCB基本算法描述如下图：

算法详解：

设定一个参数$\alpha$，这个参数决定了我们Explore的程度；
开始试验迭代；
获取每一个arm的特征向量$x_{a,t}$；
开始计算每一个arm的预估回报及其置信区间；
如果arm还从没有被试验过，那么：
用单位矩阵初始化$A_a$；
用0向量初始化$b_a$；
处理完没被试验过的arm；
计算线性参数$\theta$；
用$\theta$和特征向量$x_{a,t}$计算预估回报，同时加上置信区间宽度；
处理完每一个arm；
选择第10步中最大值对应的arm，观察真实的回报$r_t$；
更新$A_{at}$；
更新$b_{at}$；
算法结束。

python代码实现LinUCB：

class LinUCB:
    def __init__(self):
     self.alpha = 0.25 
     self.r1 = 1 # if worse -> 0.7, 0.8
        self.r0 = 0 # if worse, -19, -21
        # dimension of user features = d
        self.d = 6
        # Aa : collection of matrix to compute disjoint part for each article a, d*d
        self.Aa = {}
        # AaI : store the inverse of all Aa matrix
        self.AaI = {}
        # ba : collection of vectors to compute disjoin part, d*1
        self.ba = {}
 
        self.a_max = 0
 
        self.theta = {}
 
        self.x = None
        self.xT = None
        # linUCB
 
    def set_articles(self, art):
        # init collection of matrix/vector Aa, Ba, ba
        for key in art:
            self.Aa[key] = np.identity(self.d)
            self.ba[key] = np.zeros((self.d, 1))
            self.AaI[key] = np.identity(self.d)
            self.theta[key] = np.zeros((self.d, 1))
        # 这里更新参数时没有传入更新哪个arm，因为在上一次recommend的时候缓存了被选的那个arm，所以此处不用传入 
        # 另外，update操作不用阻塞recommend，可以异步执行        
    def update(self, reward):
        if reward == -1:
            pass
        elif reward == 1 or reward == 0:
            if reward == 1:
                r = self.r1
            else:
                r = self.r0
            self.Aa[self.a_max] += np.dot(self.x, self.xT)
            self.ba[self.a_max] += r * self.x
            self.AaI[self.a_max] = linalg.solve(self.Aa[self.a_max], np.identity(self.d))
            self.theta[self.a_max] = np.dot(self.AaI[self.a_max], self.ba[self.a_max])
        else:
        # error
            pass
        # 预估每个arm的回报期望及置信区间
    def recommend(self, timestamp, user_features, articles):
        xaT = np.array([user_features])
        xa = np.transpose(xaT)
        art_max = -1
        old_pa = 0
 
        # 获取在update阶段已经更新过的AaI(求逆结果)
        AaI_tmp = np.array([self.AaI[article] for article in articles])
        theta_tmp = np.array([self.theta[article] for article in articles])
        art_max = articles[np.argmax(np.dot(xaT, theta_tmp) + self.alpha * np.sqrt(np.dot(np.dot(xaT, AaI_tmp), xa)))]
 
        # 缓存选择结果，用于update
        self.x = xa
        self.xT = xaT
        # article index with largest UCB
        self.a_max = art_max
 
        return self.a_max

LinUCB 的重点。

LinUCB 不再是上下文无关地，像盲人摸象一样从候选臂中去选择了，而是要考虑上下文因素，比如是用户特征、物品特征和场景特征一起考虑。

每一个候选臂针对这些特征各自维护一个参数向量，各自更新，互不干扰。

每次选择时用各自的参数去计算期望收益和置信区间，然后按照置信区间上边界最大的输出结果。

观察用户的反馈，简单说就是“是否点击”，将观察的结果返回，结合对应的特征，按照刚才给出的公式，去重新计算这个候选臂的参数。

当 LinUCB 的特征向量始终取 1，每个候选臂的参数是收益均值的时候，LinUCB 就是 UCB。

高级版的 LinUCB

与简单版的相比，就是认为有一部分特征对应的参数是在所有候选臂之间共享的，所谓共享，也就是无论是哪个候选臂被选中，都会去更新这部分参数。在“Yahoo！”的应用中，物品是文章。它对特征做了一些工程化的处理，这里以此为例，可供实际应用时参考借鉴。

首先，原始用户特征有下面几个。

人口统计学：性别特征（2 类），年龄特征（离散成 10 个区间）。
地域信息：遍布全球的大都市，美国各个州。
行为类别：代表用户历史行为的 1000 个类别取值。

其次，原始文章特征有：

URL 类别：根据文章来源分成了几十个类别。
编辑打标签：编辑人工给内容从几十个话题标签中挑选出来的。
原始特征向量先经过归一化，变成单位向量。

再对原始用户特征做第一次降维，降维的方法就是利用用户特征和物品特征以及用户的点击行为去拟合一个矩阵 W。

$\phi_u^T W \phi_a^T$

就用逻辑回归拟合用户对文章的点击历史，得到的 W 直觉上理解就是：能够把用户特征映射到物品特征上，相当于对用户特征降维了，映射方法是下面这样。

$\psi_u = \phi_u^T W$

这一步可以将原始的 1000 多维用户特征投射到文章的 80 多维的特征空间。
然后，用投射后的 80 多维特征对用户聚类，得到 5 个类，文章页同样聚类成 5 个类，再加上常数 1，用户和文章各自被表示成 6 维向量。接下来就应用前面的 LinUCB 算法就是了，特征工程依然还是很有效的。

我们实际上可以考虑三类特征：U（用户），A（广告或文章），C（所在页面的一些信息）。
总结一下LinUCB算法，有以下优点：

由于加入了特征，所以收敛比UCB更快（论文有证明）；
特征构建是效果的关键，也是工程上最麻烦和值的发挥的地方；
由于参与计算的是特征，所以可以处理动态的推荐候选池，编辑可以增删文章；
特征降维很有必要，关系到计算效率。

19.【MAB问题】如何将Bandit算法与协同过滤结合使用

信息茧房

推荐系统中最经典的算法莫过于协同推荐。在技术上，Bandit 算法就是一个权衡探索和利用的好方法。如果把它结合传统的协同过滤来做推荐，那么在一定程度上就可以延缓信息茧房的到来。如何结合协同过滤的群体智慧，与 Bandit 的走一步看一步一起，让两种思想碰撞，这就是 2016 年有人提出的 COFIBA 算法。

COFIBA 算法

思想

很多的推荐场景中都有两个规律。

相似的用户对同一个物品的反馈可能是一样的。也就是对一个聚类用户群体推荐同一个 item，他们可能都会喜欢，也可能都不喜欢，同样的，同一个用户会对相似的物品反馈也会相同。这实际上就是基于用户的协同过滤基本思想。

在使用推荐系统过程中，用户的决策是动态进行的，尤其是新用户。这就导致无法提前为用户准备好推荐候选，只能“走一步看一步”，是一个动态的推荐过程。这是 Bandit 的算法基本思想。

每一个推荐候选物品，都可以根据用户对其偏好的不同，将用户分成不同的群体。然后下一次，由用户所在的群体集体帮他预估可能的收益及置信区间，这个集体就有了协同的效果，然后再实时观察真实反馈，回来更新用户的个人参数用于下次调整收益和置信区间，这就有了 Bandit 的思想在里面。
如果要推荐的候选物品较多，需要对物品聚类，就不用按照每一个物品对用户聚类，而是按照每一个物品所属的类簇对用户聚类，如此一来，物品的类簇数目相对于物品数就要大大减少。

细节

COFIBA 算法要点摘要如下：

在时刻 t，有一个用户来访问推荐系统，推荐系统需要从已有的候选池子中挑一个最佳的物品推荐给他，然后观察他的反馈，用观察到的反馈来更新挑选策略。

这里的每个物品都有一个特征向量，所以这里的 Bandit 算法是 context 相关的，只不过这里虽然是给每个用户维护一套参数，但实际上是由用户所在的聚类类簇一起决定结果的。

这里依然是用岭回归去拟合用户的权重向量，用于预测用户对每个物品的可能反馈（payoff），这一点和我们上一次介绍的 LinUCB 算法是一样的。

算法流程如下图所示：

对比LinUCB 算法，COFIBA 的不同有两点：

基于用户聚类挑选最佳的物品，即相似用户集体动态决策；
基于用户的反馈情况调整用户和物品的聚类结果。

整体算法过程如下，在针对某个用户 i，在每一次推荐时做以下事情：

首先计算用户 i 的 Bandit 参数 W，做法和 LinUCB 算法相同，但是这个参数并不直接参与到选择决策中，注意这和 LinUCB 不同，只是用来更新用户聚类。
遍历候选物品，每一个物品已经表示成一个向量 x 了。
每一个物品都对应一个物品聚类类簇，每一个物品类簇对应一个全量用户聚类结果，所以遍历到每一个物品时，就可以判断出当前用户在当前物品面前，自己属于哪个用户聚类类簇，然后把对应类簇中每个用户的 M 矩阵 (对应 LinUCB 里面的 A 矩阵)，b 向量（表示收益向量，对应 LinUCB 里面的 b 向量）加起来，从而针对这个类簇求解一个岭回归参数（类似
LinUCB 里面单独针对每个用户所做），同时计算其收益预测值和置信区间上边界。
每个待推荐的物品都得到一个预测值及置信区间上界，挑出那个上边界最大的物品作为推荐结果。
观察用户的真实反馈，然后更新用户自己的 M 矩阵和 b 向量，只更新每个用户，对应类簇里其他的不更新。

以上是 COFIBA 算法的一次决策过程。在收到用户真实反馈之后，还有两个计算过程：

更新 user 聚类；
更新 item 聚类。

更新 user 和 item 的聚类的方法如下图所示：

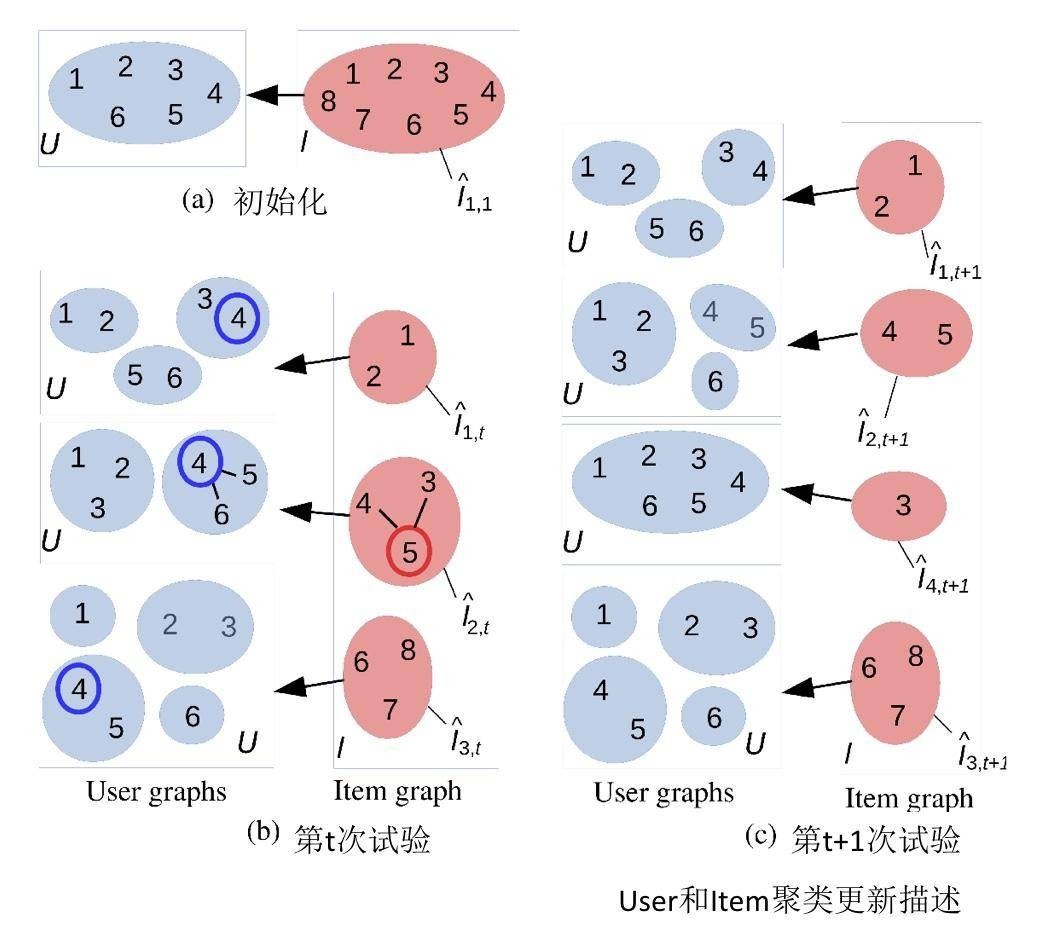
COFIBA更新类别.jpg

步骤详解：
(a) 示意图中有 6 个用户，8 个物品，初始化时，用户和物品的类簇个数都是 1。
(b) 在某一轮推荐时，推荐系统面对的用户是 4。推荐过程就是遍历 1～8 每个物品，然后在面对每个物品时，用户 4 在哪个类簇中，把对应类簇中的用户聚合起来为这个物品集体预测收益值置信上边界。这里假设最终物品 5 胜出，被推荐出去了。

在时刻 t，物品一共有 3 个聚类类簇，需要更新的用户聚类是物品 5 对应的用户 4 所在类簇。
更新方式：看看该类簇里面除了用户 4 之外的用户，对物品 5 的预期收益是不是和用户 4 相近，如果是，则保持原来的连接边，否则删除原来的连接边。删除边之后相当于就重新构建了聚类结果。
这里假设新的聚类结果由原来用户 4 所在的类簇分裂成了两个类簇：4 和 5 成一类，6 单独自成一类。

(c) 更新完用户类簇后，被推荐出去的物品 5，它对应的类簇也要更新。

更新方式是：对于每一个和物品 5 还存在连接边的物品，假如叫做物品 j，都有一个对这个物品 j 有相近收益预估值的近邻用户集合，然后看看近邻用户集合是不是和刚刚更新后的用户 4 所在的类簇相同。
是的话，保留物品 5 和物品 j 之间的连接边，否则删除。这里示意图中是物品 3 和物品 5 之间的连接边被删除。
物品 3 变成了孤家寡人一个，不再和任何物品有链接，独立后就给他初始化了一个全新的用户聚类结果：所有用户是一个类簇。

简单来说就是这样：

用协同过滤来少选可以参与决策的用户代表，用 LinUCB 算法来实际执行选择；
根据用户的反馈，调整基于用户和基于物品的聚类结果，即对物品和用户的群体代表做换届选举；
基于物品的聚类如果变化，又进一步改变了用户的聚类结果；
不断根据用户实时动态的反馈来调整用户决策参数，从而重新划分聚类结果矩阵。

再谈 EE 问题

探索和利用这一对矛盾一直客观存在，而 Bandit 算法是公认的一种比较好的解决 EE 问题的方案。
除了 Bandit 算法之外，还有一些其他的探索兴趣的办法，比如在推荐时，随机地去掉一些用户历史行为（特征）。
解决兴趣探索，势必要冒险，势必要面对用户的未知，而这显然就是可能会伤害当前用户价值的：明知道用户肯定喜欢 A，你还偏偏以某个小概率给推荐非 A。

实际上，很少有公司会采用这些理性的办法做探索，反而更愿意用一些盲目主观的方式。究其原因，可能是因为：

互联网产品生命周期短，而探索又是为了提升长期利益的，所以没有动力做；
用户使用互联网产品时间越来越碎片化，探索的时间长，难以体现出探索的价值；
同质化互联网产品多，用户选择多，稍有不慎，用户用脚投票，分分钟弃你于不顾；
已经成规模的平台，红利杠杠的，其实是没有动力做探索的。

基于这些，我们如果想在自己的推荐系统中引入探索机制，需要注意以下几点：

用于探索兴趣的物品，要保证其本身质量，纵使用户不感兴趣，也不至于引起其反感，损失平台品牌价值；
探索兴趣的地方需要产品精心设计，让用户有耐心陪你玩儿；
深度思考，这样才不会做出脑残的产品，产品不会早早夭折，才有可能让探索机制有用武之地。

Bandit 算法是一种不太常用在推荐系统的算法，究其原因，是它能同时处理的物品数量不能太多。但是，在冷启动和处理 EE 问题时，Bandit 算法简单好用，值得一试。

MBA问题.jpg