Faiss 召回详解

1 引言

向量检索普遍应用于搜索、推荐、以及CV领域，往往候选集合两集都在千万甚至上亿规模。那么，速度很容易成为瓶颈，这时候就需要牺牲一定的精度来换取速度。于是诞生了许多ANN（近邻检索）算法，例如HNSW就是其中一种。但是，不同的ANN具有各自的优劣势，本文主要介绍faiss这一工业界普遍使用的向量检索框架。

Faiss的是由FaceBook的AI团队公开的项目Facebook AI Similarity Search，是针对大规模相似度检索问题开发的一个工具，使用C++编写，有python接口，对10亿量级的索引可以做到毫秒级检索的性能。

其核心思想：把候选向量集封装成一个index数据库，加速检索TopK相似向量的过程，尽量维持召回率，其中部分索引支持GPU构建。

2 原理

Faiss框架中，需要了解k-means、PCA以及PQ等算法。但最需要了解的2个核心原理便是：

• Product Quantizer, 简称PQ.
• Inverted File System, 简称IVF.

2.1 乘积量化(PQ)原理

矢量量化方法，即vector quantization，其具体定义为: 将向量空间的点用一个有限子集来进行编码的过程。常见的聚类算法，都是一种矢量量化方法。向量量化方法又以乘积量化(PQ, Product Quantization)最为典型。

乘积量化的核心思想:分段（划分子空间）和聚类，KMeans是PQ乘积量化子空间数目为1的特例。

PQ乘积量化生成码本和量化的过程可以用如下图示来说明：

在训练阶段:

1. 针对N个训练样本，假设样本维度为128维，我们将其切分为4个子空间，则每一个子空间的维度为32维;
2. 然后我们在每一个子空间中，对子向量采用K-Means对其进行聚类(图中示意聚成256类)，这样每一个子空间都能得到一个码本，这步称为Clustering。
3. 这样训练样本的每个子段，都可以用子空间的聚类中心来近似，对应的编码即为类中心的ID(8bit)，这步称为 Assign。
4. 如图所示，通过这样一种编码方式，训练样本仅使用的很短的一个编码得以表示，从而达到量化的目的。
5. 对于待编码的样本，将它进行相同的操作，在各个子空间里使用距离它们最近类中心的id来表示它们，即完成了编码。

通过下图可以看到，作者做了相应的实验，最终发现，压缩后的类中心ID设置为m=8bit（即上述的256类）效果最好。

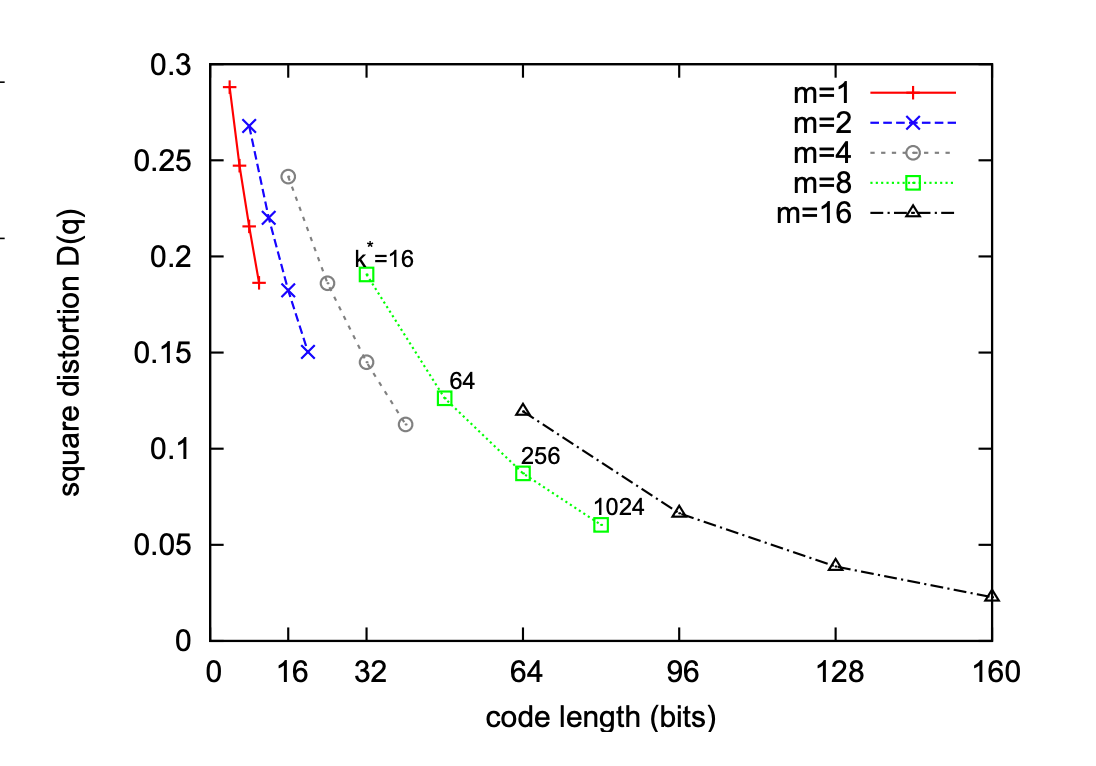
在查询阶段:

下面过程示意的是查询样本来到时，以非对称距离的方式(红框标识出来的部分)计算到dataset样本间的过程：

1. 按生成码本的过程，将其同样分成相同的子段，然后在每个子空间中，计算子段到该子空间中所有聚类中心得距离，得到距离表（维度4x256）。
2. 在计算库中某个样本到查询向量的距离时，比如编码为(124, 56, 132, 222)这个样本，我们分别到距离表中取各个子段对应的距离即可。
3. 所有子段对应的距离取出来后，将这些子段的距离求和相加，即得到该样本到查询样本间的非对称距离。
4. 所有距离算好后，排序后即得到我们最终想要的结果。（实际上距离计算节省了，但是依然要遍历排序查找）

PQ乘积量化能够加速索引的原理：即将全样本的距离计算，转化为到子空间类中心的距离计算。

• 比如上面所举的例子，原本brute-force search的方式计算距离的次数随样本数目N成线性增长，但是经过PQ编码后，对于耗时的距离计算，只要计算4x256次，几乎可以忽略此时间的消耗。
• 另外，从上图也可以看出，对特征进行编码后，可以用一个相对比较短的编码来表示样本，自然对于内存的消耗要大大小于 brute-force search 的方式。

在某些特殊的场合，我们总是希望获得精确的距离，而不是近似的距离，并且我们总是喜欢获取向量间的余弦相似度（余弦相似度距离范围在[-1,1]之间，便于设置固定的阈值），针对这种场景，可以针对PQ乘积量化得到的前top@K做一个brute-force search的排序。

2.2 倒排乘积量化（IVFPQ）原理

如果向量比较多，虽然降低了距离的计算复杂度，但是依然要便利所有的向量，需要进一步优化。倒排PQ乘积量化(IVFPQ)是PQ乘积量化的更进一步加速版。

其加速的本质依然是加速原理：为了加快查找的速度，几乎所有的ANN方法都是通过对全空间分割，将其分割成很多小的子空间，在搜索的时候，通过某种方式，快速锁定在某一（几）子空间，然后在该（几个）子空间里做遍历。

仔细观察PQ乘积量化存在一定的优化空间：

• 实际上我们感兴趣的是那些跟查询样本相近的样本（姑且称这样的区域为感兴趣区域），也就是说老老实实挨个相加其实做了很多的无用功。如果能够通过某种手段快速将全局遍历锁定为感兴趣区域，则可以舍去不必要的全局计算以及排序。
• 倒排PQ乘积量化的”倒排“，正是这样一种思想的体现，在具体实施手段上，采用的是通过聚类的方式实现感兴趣区域的快速定位，在倒排PQ乘积量化中，聚类可以说应用得淋漓尽致。

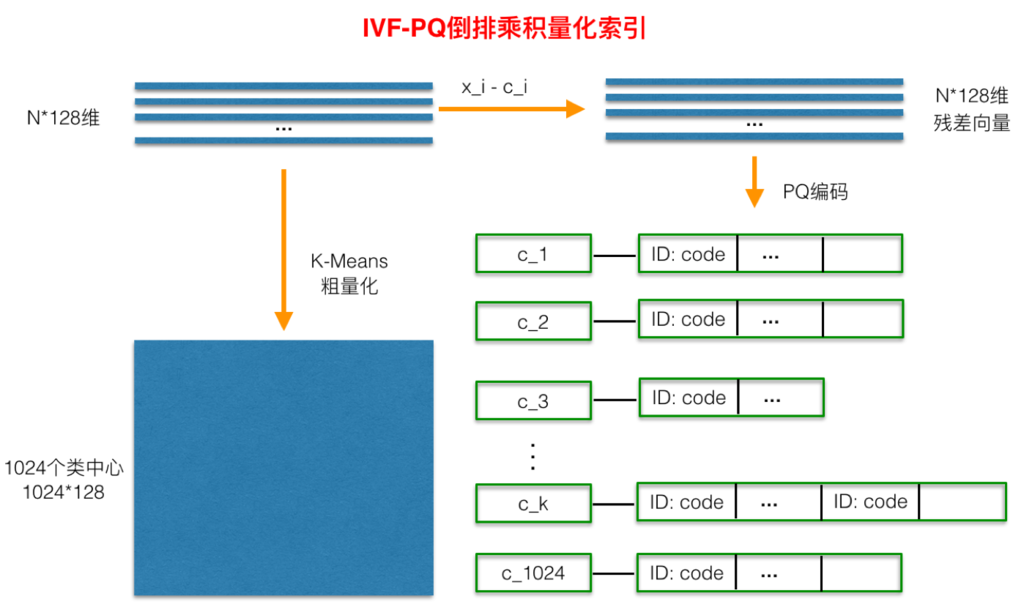
如上图所示：在PQ乘积量化之前，增加了一个粗量化过程。

具体地:

1. 先对N个训练样本采用KMeans聚类，这里聚类的数目一般设置得不应过大，一般设置为1024差不多，这种可以以比较快的速度完成聚类过程。
2. 得到了聚类中心后，针对每一个样本$x_i$，找到其距离最近的类中心$c_i$后，两者相减得到样本$x_i$的残差向量(x_i-c_i);
3. 后面剩下的过程，就是针对$(x_i-c_i)$的PQ乘积量化过程。

在查询的时候，通过相同的粗量化，可以快速定位到查询向量属于哪个$c_i$（即在哪一个感兴趣区域），也可以是多个感兴趣聚类中心，然后在该感兴趣区域按上面所述的 P Q乘积量化距离计算方式计算距离。整体流程如下图所示。

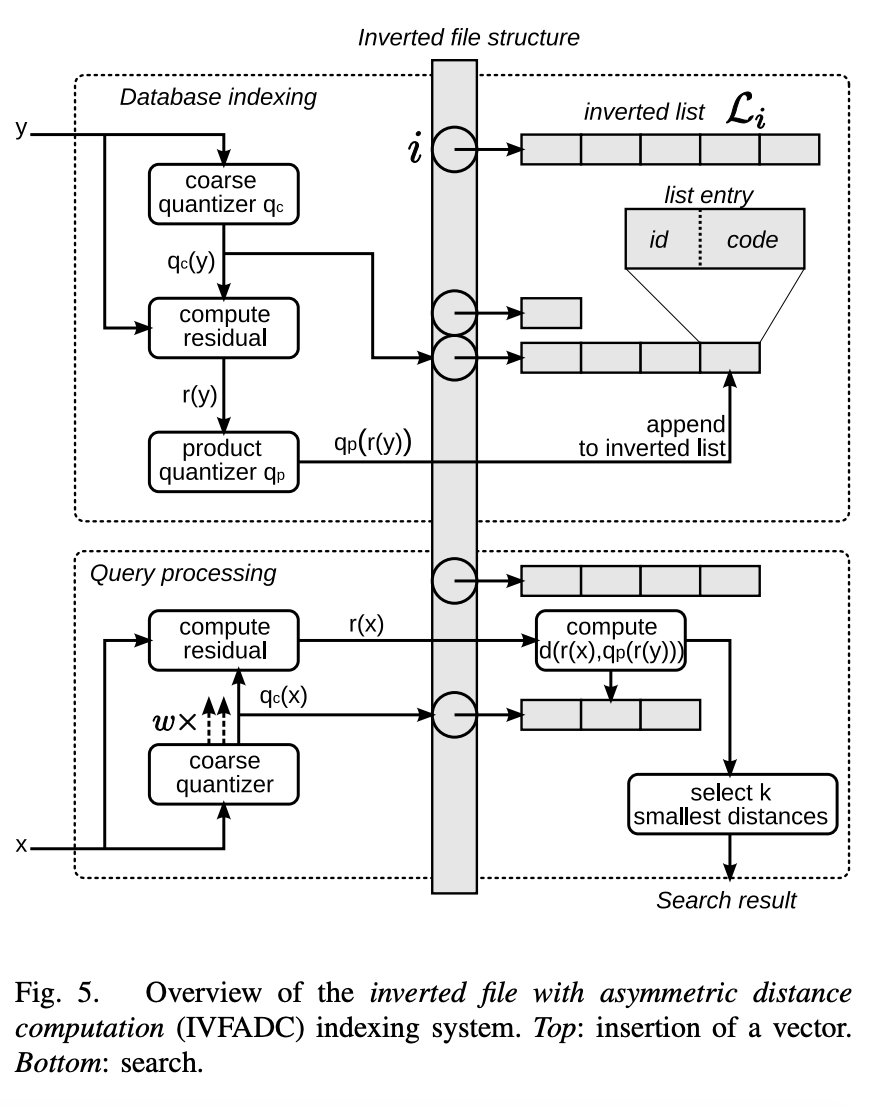
2.3 最优乘积量化（OPQ）

最优乘积量化（Optimal Product Quantization, OPQ）是PQ的一种改进版本。其改进体现在，致力于在子空间分割时，对各子空间的方差进行均衡。

用于检索的原始特征维度较高，所以实际在使用PQ等方法构建索引的时候，常会对高维的特征使用PCA等降维方法对特征先做降维处理。这样降维预处理，可以达到两个目的：

• 一是降低特征维度；
• 二是利用PCA使得在对向量进行子段切分的时候要求特征各个维度尽可能不相关。

但是这么做了后，在切分子段的时候，采用顺序切分子段仍然存在一定的问题，这个问题可以借用ITQ中的一个二维平面的例子加以说明：

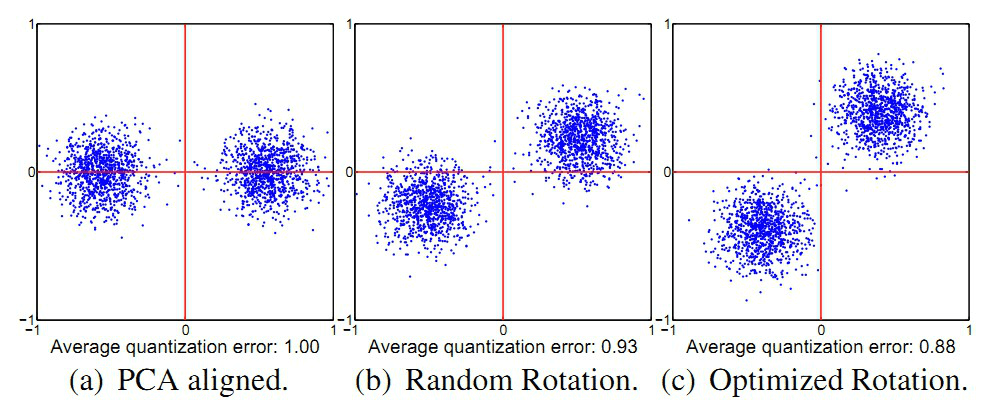
这个问题就是：

• 如上面a图所示，对于PCA降维后的二维空间，假设在做PQ的时候，将子段数目设置为2段，即切分成x和y两个子向量，然后分别在x和y上做聚类（假设聚类中心设置为2）。
• 对a图和c图聚类的结果进行比较，可以明显的发现，a图在y方向上聚类的效果明显差于c图，而PQ又是采用聚类中心来近似原始向量（这里指降维后的向量），也就是c图是我们需要的结果。

这个问题可以转化为数据方差来描述：在做PQ编码时，对于切分的各个子空间，我们应尽可能使得各个子空间的方差比较接近，最理想的情况是各个子空间的方差都相等。

解决办法：
OPQ致力于解决的问题正是对各个子空间方差的均衡。思想主要是在聚类的时候对聚类中心寻找对应的最优旋转矩阵，使得所有子空间中各个数据点到对应子空间的类中心的L2损失的求和最小。具体可以分为非参求解方法和带参求解方法，这里不再赘述。

3 code

注意faiss包的安装：conda install faiss-cpu -c pytorch

Flat ：暴力检索

优点：最准确的，召回率最高；
缺点：速度慢，占内存大。
使用情况：向量候选集很少，在50万以内，并且内存不紧张。

IVFx Flat ：倒排暴力检索

优点：IVF主要利用倒排的思想，会大大减少了检索的时间。具体可以拿出每个聚类中心下的向量ID，每个中心ID后面挂上一堆非中心向量，每次查询向量的时候找到最近的几个中心ID，分别搜索这几个中心下的非中心向量。通过减小搜索范围，提升搜索效率。
缺点：速度也还不是很快。
使用情况：向量候选集很少，在50万以内，并且内存不紧张。

PQx ：乘积量化

优点：利用乘积量化的方法，改进了普通检索，将一个向量的维度切成x段，每段分别进行检索，每段向量的检索结果取交集后得出最后的TopK。因此速度很快，而且占用内存较小，召回率也相对较高。
缺点：召回率相较于暴力检索，下降较多。
使用情况：内存及其稀缺，并且需要较快的检索速度，不那么在意召回率

IVFxPQy 倒排乘积量化

优点：工业界大量使用此方法，各项指标都均可以接受，利用乘积量化的方法，改进了IVF的k-means，将一个向量的维度切成x段，每段分别进行k-means再检索。
缺点：集百家之长，自然也集百家之短
使用情况：一般来说，各方面没啥特殊的极端要求的话，最推荐使用该方法！

import numpy as np
import faiss
from scipy.cluster.vq import vq, kmeans2
from scipy.spatial.distance import cdist


def train(vec, M, Ks):
    """
    :param vec: 向量
    :param M: 子向量组数
    :param Ks: 每组向量聚类个数
    :return: codeword: [M, Ks, Ds]，
        codeword[m][k]表示第m组子向量第k个子向量所属的聚类中心向量
    """
    Ds = int(vec.shape[1] / M)
    codeword = np.empty((M, Ks, Ds), np.float32)

    for m in range(M):
        vec_sub = vec[:, m * Ds: (m + 1) * Ds]
        # 第m组子向量vec_sub聚成Ks类
        # kmeans2返回两个结果，第一个是原始向量归属类目的中心向量，第二个是类目ID
        codeword[m], label = kmeans2(vec_sub, Ks)
    return codeword


def encode(codeword, vec):
    """
    :param codeword: 码本，shape为[M, Ks, Ds]
    :param vec: 原始向量
    :return: pqcode: pq编码结果,
        shape为[N, M]，每个原始向量用M组子向量的聚类中心ID表示
    """
    M, Ks, Ds = codeword.shape
    # pq编码shape为[N, M]
    pqcode = np.empty((vec.shape[0], M), np.int64)
    for m in range(M):
        vec_sub = vec[:, m * Ds: (m + 1) * Ds]
        # 第m组子向量
        # 第m组子向量中每个子向量在第m个码本中查找距离最近的
        pqcode[:, m], dist = vq(vec_sub, codeword[m])
    return pqcode


def search(codeword, pqcode, query):
    """
    :param codeword:
    :param pqcode: pq编码结果, shape为[N, M]，每个原始向量用M组子向量的聚类中心ID表示
    :param query: 查询向量[1, d]
    :return: dist：查询向量与原始向量的距离，shape为[N,]
    """
    M, Ks, Ds = codeword.shape
    # 距离向量表, [M, Ks]
    dist_table = np.empty((M, Ks))
    for m in range(M):
        query_sub = query[m * Ds: (m + 1) * Ds]
        # query_sub向量与第m个码本每个向量距离
        dist_table[m, :] = cdist([query_sub], codeword[m], 'sqeuclidean')[0]

    # dist_table[range(M), pqcode] 为 query向量与原始向量在每个子向量的聚类，shape为[N, M]
    # 每组子向量距离相加
    dist = np.sum(dist_table[range(M), pqcode], axis=1)
    return dist


def PQmain():
    # 数据量
    N = 50000
    # 向量维度
    d = 128
    # 每组子向量聚类个数
    Ks = 32
    # 训练向量[N, d]
    vec_train = np.random.random((N, d))
    # 查询向量[1, d]
    # mock 第100个是距离查询向量最近的
    selected_vec = vec_train[100]
    query_vec = selected_vec + [np.random.uniform(-0.001, 0.001) for _ in range(d)]
    query = np.random.random((1, d))
    # 子向量组数
    M = 4

    # 对原始向量划分子向量组，并对每组子向量进行聚类
    codeword = train(vec_train, M, Ks)
    # pq编码
    pqcode = encode(codeword, vec_train)
    # 查询向量
    dist = search(codeword, pqcode, query_vec)

    sorted_dist = sorted(enumerate(dist), key=lambda x: x[1])
    print(sorted_dist[0])

def test_IndexFlatL2(vec_train, query, top_k=5):
    """
    暴力检索
    """
    N, d = vec_train.shape
    # 1. 创建索引
    index = faiss.IndexFlatL2(d)
    # 2. 添加数据集
    index.add(vec_train)
    # 3. 检索
    dist_list, label_list = index.search(np.array([query]), k=top_k)
    print("=" * 8 + "FlatL2 recall top %d is" % top_k + "=" * 8)
    print("dist:" + str(dist_list))
    print("index:" + str(label_list))


def test_IndexIVFFlat(vec_train, query_vec, top_k=5):
    """
    通过创建倒排索引优化
    流程：使用k-means对train向量进行聚类，查询时query_vec所归属的类目中进行检索
    """
    nlist = 100  # 聚类中心的个数
    N, d = vec_train.shape
    quantizer = faiss.IndexFlatL2(d)  # the other index
    index = faiss.IndexIVFFlat(quantizer, d, nlist, faiss.METRIC_L2)
    # 添加 训练集
    index.train(vec_train)
    index.add(vec_train)
    # 检索
    query_vec = np.reshape(query_vec, [-1,d])
    D, I = index.search(query_vec, top_k)
    print("=" * 8 + "IVFFlat recall top %d is" % top_k + "=" * 8)
    print("dist:" + str(D))
    print("index:" + str(I))

def test_IndexIVFPQ(vec_train, query_vec, top_k=10):
    """
    通过创建倒排索引优化
    流程：使用k-means对train向量进行聚类，查询时query_vec所归属的类目中进行检索
    """
    nlist = 100  # 聚类中心的个数
    m = 8
    N, d = vec_train.shape
    quantizer = faiss.IndexFlatL2(d)  # the other index
    index = faiss.IndexIVFPQ(quantizer, d, nlist, m, 8)
    # 添加 训练集
    index.train(vec_train)
    index.add(vec_train)
    # 检索
    query_vec = np.reshape(query_vec, [-1,d])
    D, I = index.search(query_vec, top_k)
    print("="*8 + "IVFPQ recall top %d is" % top_k+"="*8)
    print("dist:" + str(D))
    print("index:" + str(I))

def faissmain():
    # 数据量
    N = 50000
    # 向量维度
    d = 128
    vec_train = np.ascontiguousarray(np.random.random((N, d)), np.float32)

    # mock 第100个是距离查询向量最近的
    selected_vec = vec_train[100]
    query_vec = selected_vec + [np.random.uniform(-0.001, 0.001) for _ in range(d)]
    query_vec = np.ascontiguousarray(query_vec, np.float32)
    # 1. 暴力检索，全量检索
    test_IndexFlatL2(vec_train, query_vec)
    # 2. 倒排索引
    test_IndexIVFFlat(vec_train, query_vec)
    # 3. 倒排PQ
    test_IndexIVFPQ(vec_train, query_vec)


if __name__ == "__main__":
    PQmain()
    faissmain()

4 相关拓展

IndexIVFPQ（”IVFx,PQy”）的性能损失来自于向量压缩和倒排列表两部分。如果IndexIVFPQ的精度太低，可以：设置nprobe为nlist，以搜索整个数据集，然后查看其性能。请注意，默认nprobe值为1。

单个向量检索的速度慢，Faiss针对批量搜索进行了优化：

• 矩阵-矩阵乘法通常比对应数量的矩阵-向量乘法快得多
• 搜索并行化
• 采用多线程同时执行多个搜索，以完全占用计算机的cores

Faiss不支持字符串ID或in64以外的任何数据类型。

不同框架的召回效果对比如下图，更全的对比可参考ann-Benchmarking Results：

参考文献：

A Survey of Product Quantization
Product quantization for nearest neighbor search
Faiss原理介绍
faiss原理（Product Quantization）
搜索召回 | Facebook: 亿级向量相似度检索库Faiss原理+应用
Fiass - 常见问题总结
推荐系统的向量检索工具: Annoy & Faiss
topk相似度性能比较（kd-tree、kd-ball、faiss、annoy、线性搜索）
annoy(快速近邻向量搜索包)学习小记 - pip命令学习与annoy基础使用

---