布隆过滤器(Bloom Filter)

1 背景

在实际工作中，我们经常涉及判断一个对象或者数据是否存在于内存或者数据库。往往大家会想到HashMap，但是这时候有一个问题,存储容量占比高，考虑到负载因子的存在，通常空间是不能被用满的，而一旦你的值很多例如上亿的时候，可行性就差了。
另一方面，如果很多请求是在请求数据库根本不存在的数据,那么数据库就要频繁响应这种不必要的IO查询,如果再多一些,数据库大多数IO都在响应这种毫无意义的请求操作,为了解决这一个问题，过滤器由此诞生！

2 布隆过滤器

过滤原理：布隆过滤器(Bloom Filter)大概的思路就是,当你请求的信息来的时候,先检查一下你查询的数据我这有没有,有的话将请求压给数据库,没有的话直接返回。

布隆过滤器是一个 bit 向量或者说 bit 数组。

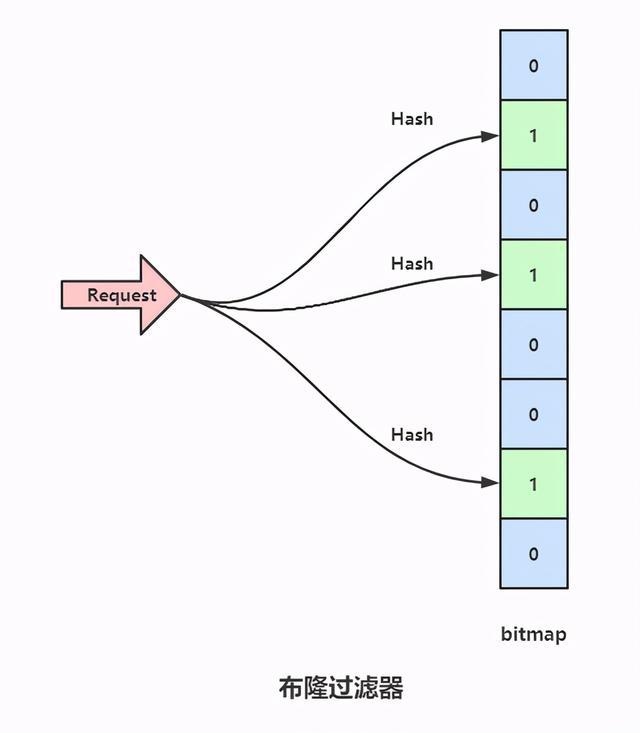
如图,一个bitmap用于记录,bitmap原始数值全都是0,当一个数据存进来的时候,用三个Hash函数分别计算三次Hash值,并且将bitmap对应的位置设置为1,上图中,bitmap 的1,3,6位置被标记为1,这时候如果一个数据请求过来,依然用之前的三个Hash函数计算Hash值,如果是同一个数据的话,势必依旧是映射到1,3,6位,那么就可以判断这个数据之前存储过,如果新的数据映射的三个位置,有一个匹配不上,加入映射到1,3,7位,由于7位是0,也就是这个数据之前并没有加入进数据库,所以直接返回。

3 存在的问题

3.1 误判

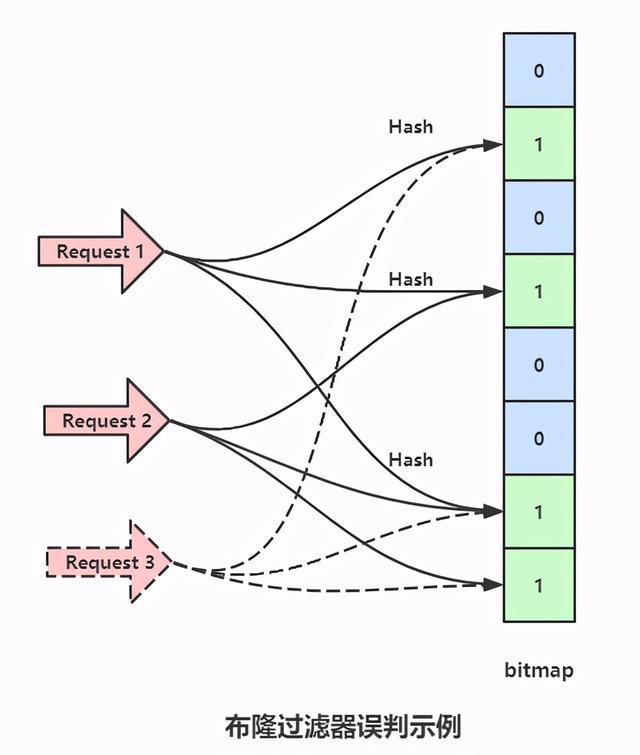
如上图所示，假如有这么一个情景,放入数据包1时,将bitmap的1,3,6位设置为了1,放入数据包2时将bitmap的3,6,7位设置为了1,此时一个并没有存过的数据包请求3,做三次哈希之后,对应的bitmap位点分别是1,6,7,这个数据之前并没有存进去过,但是由于数据包1和2存入时将对应的点设置为了1,所以请求3也会压到数据库上,这种情况,会随着存入的数据增加而增加。

所以，布隆过滤器只能够得出两种结论：

• 当hash对应的位置出现0的时候，就表明一定不存在；
• 当全是1的时候，由于误判的可能，只能表明可能存在。

3.2 无法删除

布隆过滤器无法删除的原因有二：

1. 由于有误判的可能,并不确定数据是否存在数据库里,例如数据包3。
2. 当你删除某一个数据包对应位图上的标志后,可能影响其他的数据包。
   （例如上面例子中,如果删除数据包1,也就意味着会将bitmap1,3,6位设置为0,此时数据包2来请求时,会显示不存在,因为3,6两位已经被设置为0。）

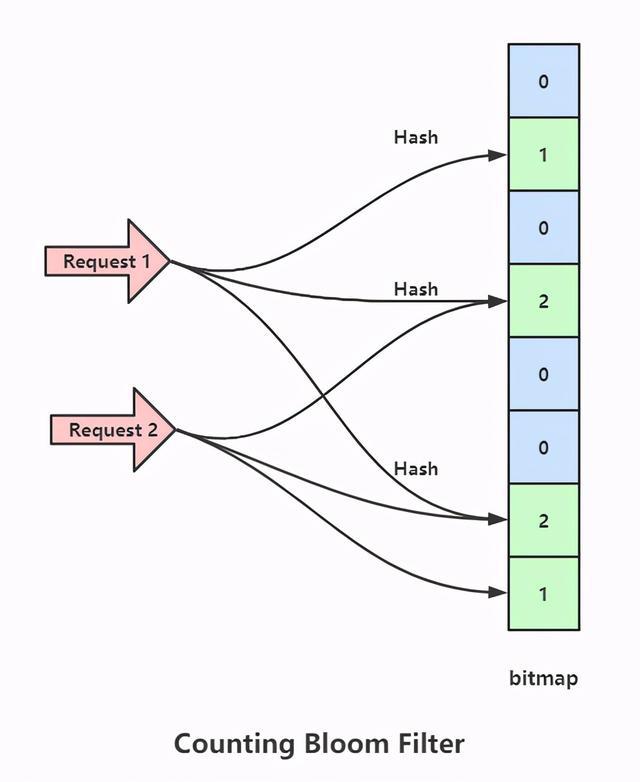
为此还出现了一个改进版的布隆过滤器，即 Counting Bloom filter，可以用来测试元素计数个数是否绝对小于某个阈值，如下图所示。这个过滤器的思路是将布隆过滤器的bitmap更换成数组,当数组某位置被映射一次时就+1,当删除时就-1,这样就避免了普通布隆过滤器删除数据后需要重新计算其余数据包Hash的问题,但实际上也无法解决删除的问题。原因是，由于一开始就存在误判的可能，如果在删除的时候，一个本来不存在的由于误判而进行了删除，就会使得其他原本正确的出现错误计数。

这个问题造就了其软肋，布隆过滤器就好比是印迹，来过来就会有痕迹，就算走了也无法清理干净。比如你的系统里本来只留下 1kw 个元素，但是整体上来过了上亿的流水元素，布隆过滤器很无奈，它会将这些流失的元素的印迹也会永远存放在那里。随着时间的流失，这个过滤器会越来越拥挤，直到有一天你发现它的误判率太高了，不得不进行重建。

3.3 其他问题

查询性能弱
是因为布隆过滤器需要使用多个 hash 函数探测位图中多个不同的位点，这些位点在内存上跨度很大，会导致 CPU 缓存行命中率低。

空间效率低
是因为在相同的误判率下，布谷鸟过滤器的空间利用率要明显高于布隆，空间上大概能节省 40% 多。不过布隆过滤器并没有要求位图的长度必须是 2 的指数，而布谷鸟过滤器必须有这个要求。从这一点出发，似乎布隆过滤器的空间伸缩性更强一些。

3.4 参数选择

布隆过滤器在构建时，有两个重要的参数，一个是Hash函数的个数k，另一个是 bit 数组的大小m。

过小的布隆过滤器很快所有的 bit 位均为 1，那么查询任何值都会返回“可能存在”，起不到过滤的目的了。布隆过滤器的长度会直接影响误报率，布隆过滤器越长其误报率越小。
另外，哈希函数的个数也需要权衡，个数越多则布隆过滤器 bit 位置位 1 的速度越快，且布隆过滤器的效率越低；但是如果太少的话，那我们的误报率会变高。

我们参考如下一个图：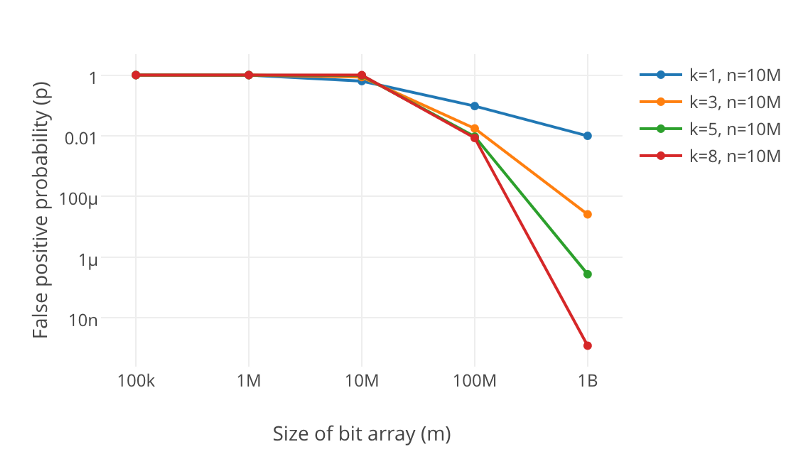

其中：

k是Hash函数的个数；
m是布隆过滤器数组的长度；
n是需要插入元素的个数；
p是误报率。

3.5 误报率

如果 m 是位数组中的比特数，则在插入元素期间某一特定比特位不被某个哈希函数设置为 1 的概率是：

$$1 - \frac{1}{m}$$

如果哈希函数的数量是 k，则通过 k 个哈希函数都未将该位设置为 1 的概率是：

$$(1 - \frac{1}{m})^k$$

那么，如果我们插入了 n 个元素，某个位为1的概率，我们利用反向概率就可以求得为：

$$1 - (1 - \frac{1}{m})^{kn}$$

现在我们要判断一个元素是否在集合中，假设这个元素本不在集合中，理论上来讲，经过 k 个哈希函数计算后得到的位数组的 k 个位置的值都应该是 0，如果发生了误判，即这 k 个位置的值都为 1，这就对应着误判率如下：

$$p=(1 - [1 - \frac{1}{m}]^{kn})^k \approx (1 - e^{-\frac{kn}{m}})^k$$

参考极限公式：

$$\lim_{x \to \infty} (1 - \frac{1}{x})^{-x}=e$$

3.6 最优的k

这里存在两个互斥：

• 如果哈希函数的个数多，那么在对一个不属于集合的元素进行查询时得到0的概率就大；
• 一方面，如果哈希函数的个数少，那么位数组中的0就多。

为了得到最优的哈希函数个数，我们需要根据上一节中的错误率公式进行计算。
我们首先对误判率两边取对数：

$$ln(p) = k ln(1-e^{-\frac{kn}{m}})$$

我们的目的是求最优的k，且最优就表明误判率p要是最小，所以两边对k求导：

$$\frac{1}{p} \cdot p' = ln(1 - e^{-\frac{nk}{m}}) + \frac{k e^{-\frac{nk}{m}} \frac{n}{m}}{1 - e^{-\frac{nk}{m}}}$$

另$p’=0$就有：

$$ln(1 - e^{-\frac{nk}{m}}) + \frac{k e^{-\frac{nk}{m}} \frac{n}{m}}{1 - e^{-\frac{nk}{m}}} = 0$$ $$(1 - e^{-\frac{nk}{m}}) \cdot ln(1 - e^{-\frac{nk}{m}}) = -k e^{-\frac{nk}{m}} \frac{n}{m}$$ $$(1 - e^{-\frac{nk}{m}}) \cdot ln(1 - e^{-\frac{nk}{m}}) = e^{-\frac{nk}{m}}(-\frac{nk}{m})$$

所以：

$$1 - e^{-\frac{nk}{m}} = e^{-\frac{nk}{m}}$$ $$e^{-\frac{nk}{m}} = 1/2$$ $$\frac{kn}{m} = ln2$$ $$k = \frac{m}{n}ln2$$

3.7 最优的m

根据上面求出的最优k，我们带入误判率p的公式就有：

$$p=(1 - e^{-\frac{kn}{m}})^k=(1 - e^{-(\frac{m}{n}ln2)\frac{n}{m}})^k=\frac{1}{2}^k$$

将最优的k代入：

$$p = 2^{-ln2 \cdot\frac{m}{n}}$$

两边同时取ln就有：

$$lnp = ln2 \cdot (-ln2)\frac{m}{n}$$ $$m = -\frac{n \cdot lnp}{(ln2)^2}$$

3.8 估算 BF 的元素数量n

$$n = -\frac{m}{k}ln(1 - \frac{t}{m})$$

其中 n 是估计 BF 中的元素个数，t 是位数组中被置为 1 的位的个数。

4 代码参考

import mmh3
from bitarray import bitarray


# zhihu_crawler.bloom_filter

# Implement a simple bloom filter with murmurhash algorithm.
# Bloom filter is used to check wether an element exists in a collection, and it has a good performance in big data situation.
# It may has positive rate depend on hash functions and elements count.



BIT_SIZE = 5000000

class BloomFilter:
    
    def __init__(self):
        # Initialize bloom filter, set size and all bits to 0
        bit_array = bitarray(BIT_SIZE)
        bit_array.setall(0)

        self.bit_array = bit_array
        
    def add(self, url):
        # Add a url, and set points in bitarray to 1 (Points count is equal to hash funcs count.)
        # Here use 7 hash functions.
        point_list = self.get_postions(url)

        for b in point_list:
            self.bit_array[b] = 1

    def contains(self, url):
        # Check if a url is in a collection
        point_list = self.get_postions(url)

        result = True
        for b in point_list:
            result = result and self.bit_array[b]
    
        return result

    def get_postions(self, url):
        # Get points positions in bit vector.
        point1 = mmh3.hash(url, 41) % BIT_SIZE
        point2 = mmh3.hash(url, 42) % BIT_SIZE
        point3 = mmh3.hash(url, 43) % BIT_SIZE
        point4 = mmh3.hash(url, 44) % BIT_SIZE
        point5 = mmh3.hash(url, 45) % BIT_SIZE
        point6 = mmh3.hash(url, 46) % BIT_SIZE
        point7 = mmh3.hash(url, 47) % BIT_SIZE


        return [point1, point2, point3, point4, point5, point6, point7]

参考文章：
布隆过滤器(Bloom Filter)的原理和实现
聊聊Redis布隆过滤器与布谷鸟过滤器？一文避坑
Counting Bloom Filter 的原理和实现
详解布隆过滤器的原理，使用场景和注意事项