1 背景
在了解了布隆过滤器的缺点之后,如果想要解决就可以来学习一下布谷鸟过滤器。其最早是在2001年的论文《Cuckoo Filter: Practically Better Than Bloom》中提出的。论文中也很直接的抨击布隆过滤器的缺点,表明自己可以有效支持反向删除操作。
2 原理
先来介绍最简单的布谷鸟过滤器的工作原理。假设我们有:
- 两个Hash表,T1和T2;
- 两个Hash函数,H1和H2。
当一个不存在的元素需要进行插入的时候:
- 先使用H1计算出其在T1的位置,如果空就插入;
- 如果不空,就再利用H2计算其在T2的位置,如果空就放入;
- 如果依然不空,那就
鸠占鹊巢,把当前位置的元素踢出去,再把待插入的元素插入即可。这也是布谷鸟过滤器名称的来源。
以上就是布谷鸟过滤器的主要原理,看到这里肯定各种疑问:
被踢出的怎么办?会不会存在循环踢出?等等问题,研究人员也都进行了解决。
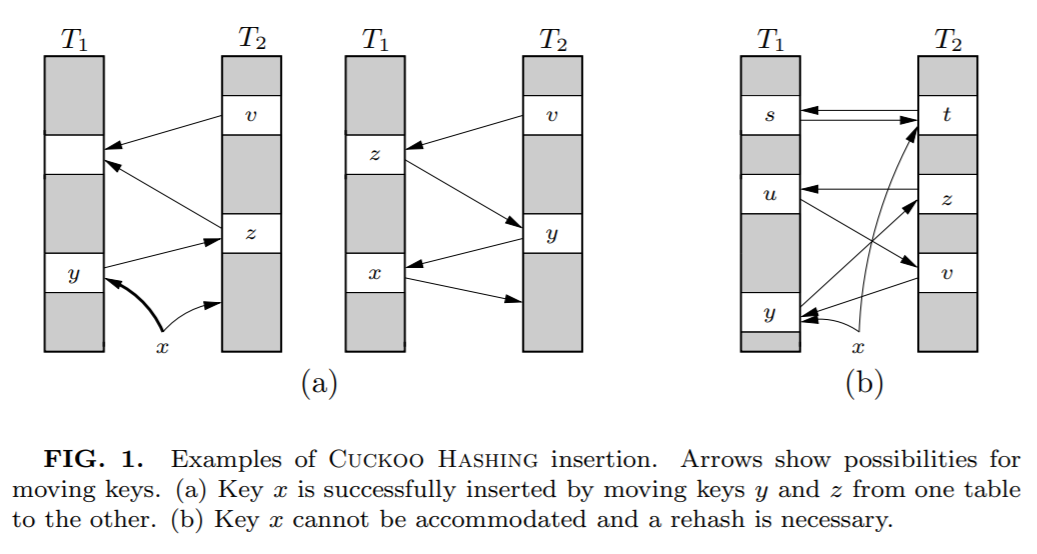
首先,不同于布谷鸟的是,布谷鸟哈希算法会帮这些受害者(被挤走的数据)寻找其它的位置。参考上面论文中的图(a):
当x想要插入的时候,发现在T1和T2中对应的位置都存在了元素,那就随机把 T1 表对应位置上的 y 踢出去吧,而 y 的另一个位置被 z 元素占领了。于是 y 毫不留情把 z 也踢了出去。z 发现自己的备用位置还空着(虽然这个备用位置也是元素 v 的备用位置),赶紧就位。
经过上述的插入过程后,整个数据结构就从(a)图中的左变成了右。这种类似于套娃的解决方式看是可行,但是总是有出现循环踢出导致放不进 x 的问题。比如上图中的(b)。
当遇到这种情况时候,说明布谷鸟 hash 已经到了极限情况,应该进行扩容,或者 hash 函数的优化。所以,你再次去看伪代码的时候,你会明白里面的 MaxLoop 的含义是什么了。这个 MaxLoop 的含义就是为了避免相互踢出的这个过程执行次数太多,设置的一个阈值。
3 优化
3.1 思路
看过上述的原理,相信依然对其性能和效果存在质疑。这里首先抛出论文中提到的短处。
虽然
MaxLoop能够避免太多循环踢出,但是这使得在完美的情况下,也就是没有发生哈希冲突之前,它的空间利用率最高只有 50%。
对于上述的问题,一般会有下面的优化方法:
- 增加 hash 函数,这样可以大大降低碰撞的概率,将空间利用率提高到 95% 左右。
- 在数组的每个位置上挂上多个座位,这样即使两个元素被 hash 在了同一个位置,也可以随意放一个。这种方案的空间利用率只有 85% 左右,但是查询效率会很高。
3.2 特殊的 hash 函数
论文在实际的优化中,一个很重要的就是构建了特殊的 Hash 函数。回忆一下布谷鸟 Hash,它存储的是插入元素的原始值,比如 x 会经过两个 hash 函数,如果我们记数组的长度为 L,那么就是这样的:
- p1 = H1(x) % L
- p2 = H2(x) % L
而布谷鸟过滤器计算位置时候实际上是:
- H1(x) = Hash(x)
- H2(x) = H1(x) $\oplus$ Hash(x’s fingerprint)
可以看到,虽然有两个Hash函数,但实际上内部只有一个Hash函数构成,在H2中使用了H1和待插入元素 x 的指纹Hash结果,然后再做异或运算。
指纹其实就是插入的元素进行一个 Hash 计算,而 Hash 计算的产物就是 几个 bit 位。布谷鸟过滤器里面存储的就是元素的“指纹”。删除数据的时候,也只是抹掉该位置上的“指纹”而已。
注意:异或运算确保了一个重要的性质,这两个位置具有对偶性。
只要保证 Hash(x’s fingerprint) !=0,那么就可以确保 H2!=H1,也就可以确保,不会出现自己踢自己的死循环问题。
为什么要对“指纹”进行一个 hash 计算之后再进行异或运算呢?
如果不进行 hash 计算,假设“指纹”的长度是 8bit,那么其对偶位置算出来,距离当前位置最远也才 256。所以,对“指纹”进行哈希处理可确保被踢出去的元素,可以重新定位到哈希表中完全不同的存储桶中,从而减少哈希冲突并提高表利用率。
它没有对数组的长度进行取模,那么它怎么保证计算出来的下标一定是落在数组中的呢?
其强制数组的长度必须是 2 的指数倍。一定是这样的:10000000…(n个0)。这个限制带来的好处就是,进行异或运算时,可以保证计算出来的下标一定是落在数组中的。
3.3 空间利用率
由于是对元素进行 hash 计算,那么必然会出现“指纹”相同的情况,也就是会出现误判的情况。没有存储原数据,所以牺牲了数据的准确性,但是只保存了几个 bit,因此提升了空间效率。
在完美的情况下,也就是没有发生哈希冲突之前,它的空间利用率最高只有 50%。因为没有发生冲突,说明至少有一半的位置是空着的。这个比率还是很低的,前面提到了优化方案,论文中也是基于只有2个Hash的条件下来进行优化的,也即增加数组的维度。
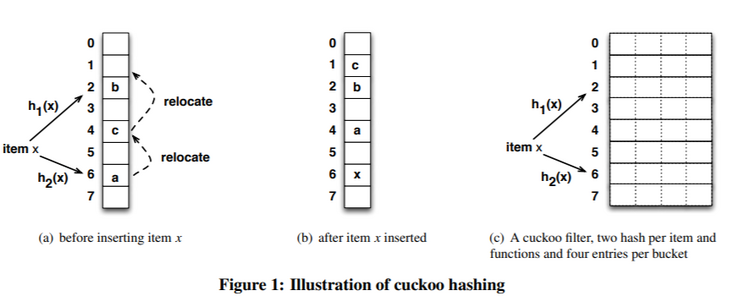
参考上面论文中的图(c),我们可以发现对数组进行展开,从一维变成了二维,这样每个位置可以放4个元素了。如此,论文中表述到,当 hash 函数固定为 2 个的时候,如果一个下标只能放一个元素,那么空间利用率是 50%。
但是如果一个下标可以放 2,4,8 个元素的时候,空间利用率就会飙升到 84%,95%,98%。
3.4 最后的弊端
布谷鸟过滤器整个了解下来,看起来一切都是这么的完美。各项指标都比布隆过滤器好,主打的是支持删除的操作。但实际上其依然存在不小的弊端。
对重复数据进行限制:如果需要布谷鸟过滤器支持删除,它必须知道一个数据插入过多少次。不能让同一个数据插入 kb+1 次。其中 k 是 Hash 函数的个数,b 是一个下标的位置能放几个元素。
举例:比如 2 个 hash 函数,一个二维数组,它的每个下标最多可以插入 4 个元素。那么对于同一个元素,最多支持插入 8 次。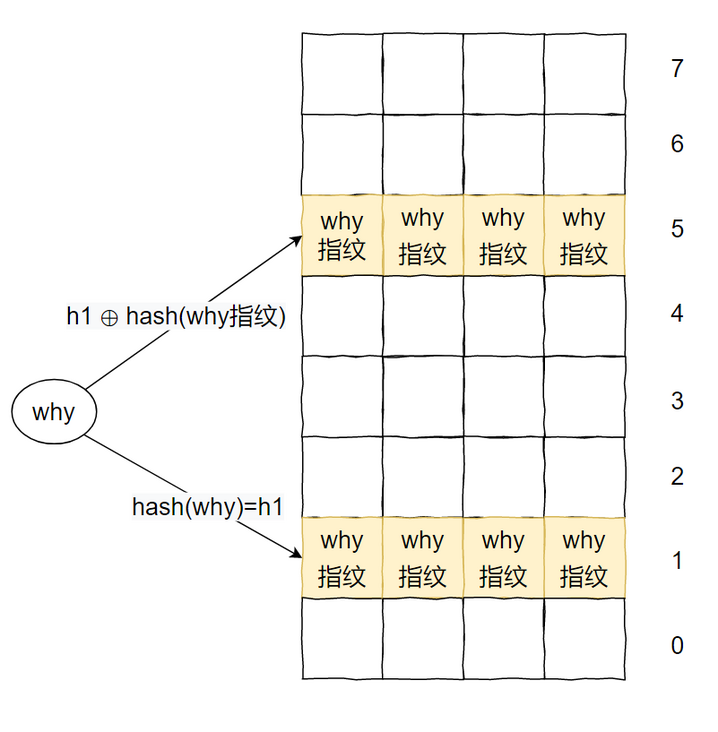
why 已经插入了 8 次了,如果再次插入一个 why,则会出现循环踢出的问题,直到最大循环次数,然后返回一个 false。想要避免这个问题,就需要维护一个记录表,记录每个元素插入的次数就行了。但是这成本一下子就大了起来。
虽然布谷鸟过滤器也不算完美无暇,但是从技术上和实际应用上看,这无异又是人类的一次技术迭代。下面的图是各种过滤器的指标对比。
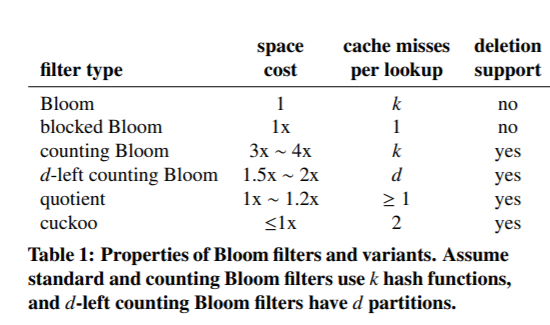
补充一个冷知识,虽然布谷鸟过滤器在2001年就被大佬 Burton Howard Bloom 提出来了,不少海内外博主一直想要看看这位大佬是和容颜。但是,海内外全网都没有,是一个彻彻底底的低调技术大佬。
参考文章
布隆,牛逼!布谷鸟,牛逼!
聊聊Redis布隆过滤器与布谷鸟过滤器?一文避坑
