深度学习中的激活函数们

1 背景

本文参考多方资料总结了一下当前在深度模型中常遇到的几种激活函数。

在神经网络中，激活函数主要有两个用途：

• 引入非线性
• 充分组合特征

其中非线性激活函数允许网络复制复杂的非线性行为。正如绝大多数神经网络借助某种形式的梯度下降进行优化，激活函数需要是可微分（或者至少是几乎完全可微分的）。此外，复杂的激活函数也许产生一些梯度消失或爆炸的问题。因此，神经网络倾向于部署若干个特定的激活函数（identity、sigmoid、ReLU 及其变体）。
因此，神经网络中激励函数的作用通俗上讲就是将多个线性输入转换为非线性的关系。如果不使用激励函数的话，神经网络的每层都只是做线性变换，即使是多层输入叠加后也还是线性变换。通过激励函数引入非线性因素后，使神经网络的表达能力更强了。

2 常见激活函数

下面是多个激活函数的图示及其一阶导数，图的右侧是一些与神经网络相关的属性。

单调性（Montonic）： 单调性使得在激活函数处的梯度方向不会经常改变，从而让训练更容易收敛

连续性（Continuous）：个人认为作者想表达可微性，可微性保证了在优化中梯度的可计算性

非饱和性（saturation）：饱和指的是在某些区间梯度接近于零（即梯度消失），使得参数无法继续更新的问题。

在深度神经网络中，前面层上的梯度是来自于后面层上梯度的乘乘积。当存在过多的层次时，就出现了内在本质上的不稳定场景，如梯度消失和梯度爆炸

梯度消失（Vanishing Gradient）：某些区间梯度接近于零；前面的层比后面的层梯度变化更小，故变化更慢，从而引起了梯度消失问题

梯度爆炸(Exploding Gradient): 某些区间梯度接近于无穷大或者权重过大；前面层比后面层梯度变化更快，会引起梯度爆炸问题

2.1 Step

它的函数和倒数表达式是：

$$f(x)= \left\{\begin{matrix} 1 \quad for \ x \ge 0 \\ 0 \quad for \ x < 0 \end{matrix}\right.$$ $$f'(x)= \left\{\begin{matrix} 0 \quad for \ x \ne 0 \\ ? \quad for \ x = 0 \end{matrix}\right.$$

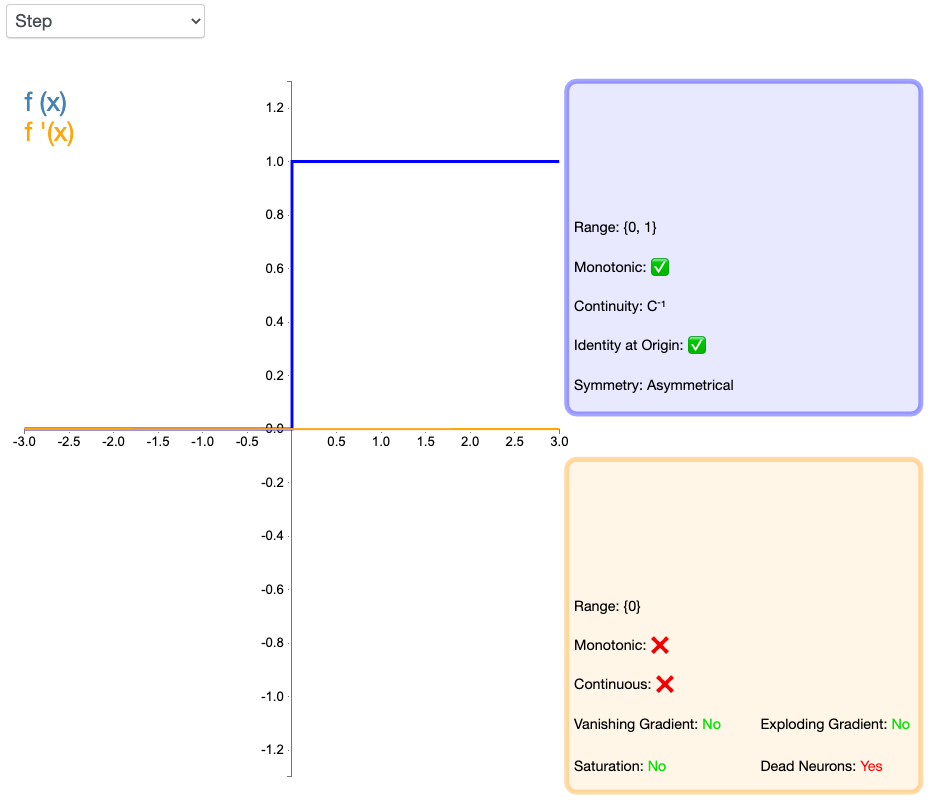
激活函数 Step 更倾向于理论而不是实际，它模仿了生物神经元要么全有要么全无的属性。它无法应用于神经网络，因为其导数是 0（除了零点导数无定义以外），这意味着基于梯度的优化方法并不可行。

2.2 Identity

$$Identity(x)=x$$ $$Identity'(x)=1$$

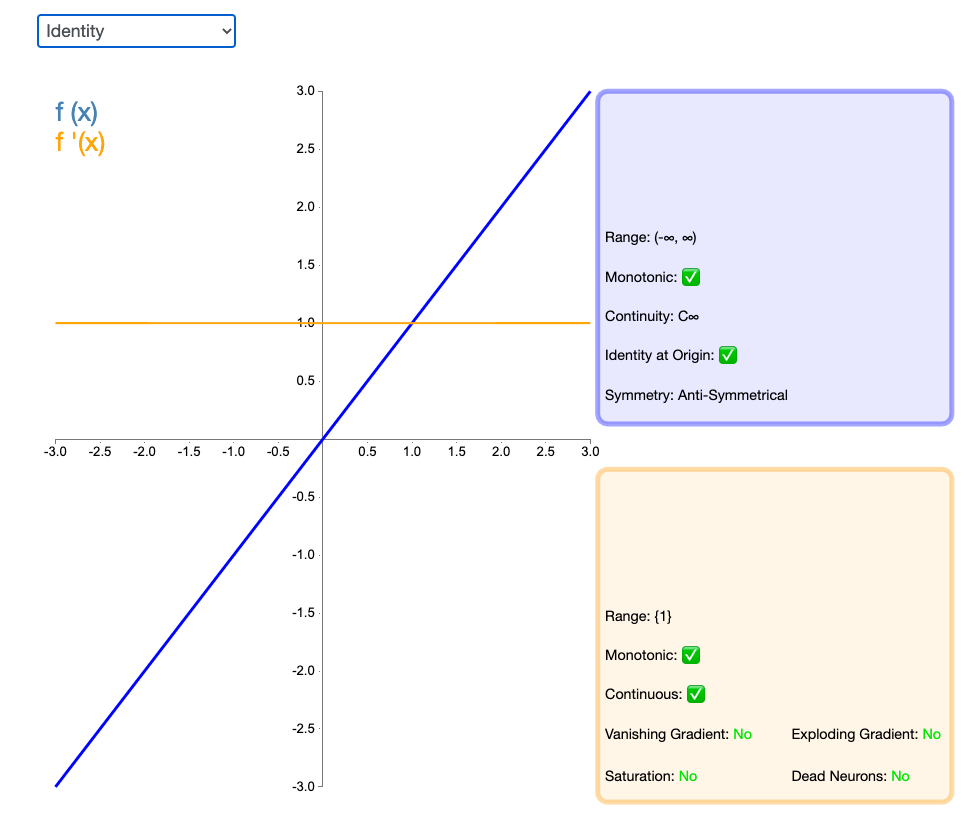
通过激活函数 Identity，节点的输入等于输出。它完美适合于潜在行为是线性（与线性回归相似）的任务。当存在非线性，单独使用该激活函数是不够的，但它依然可以在最终输出节点上作为激活函数用于回归任务。

2.3 ReLU

$$ReLU(x)= \left\{\begin{matrix} x \quad for \ x \ge 0 \\ 0 \quad for \ x < 0 \end{matrix}\right.$$ $$ReLU'(x)= \left\{\begin{matrix} 1 \quad for \ x \ge 0 \\ 0 \quad for \ x < 0 \end{matrix}\right.$$

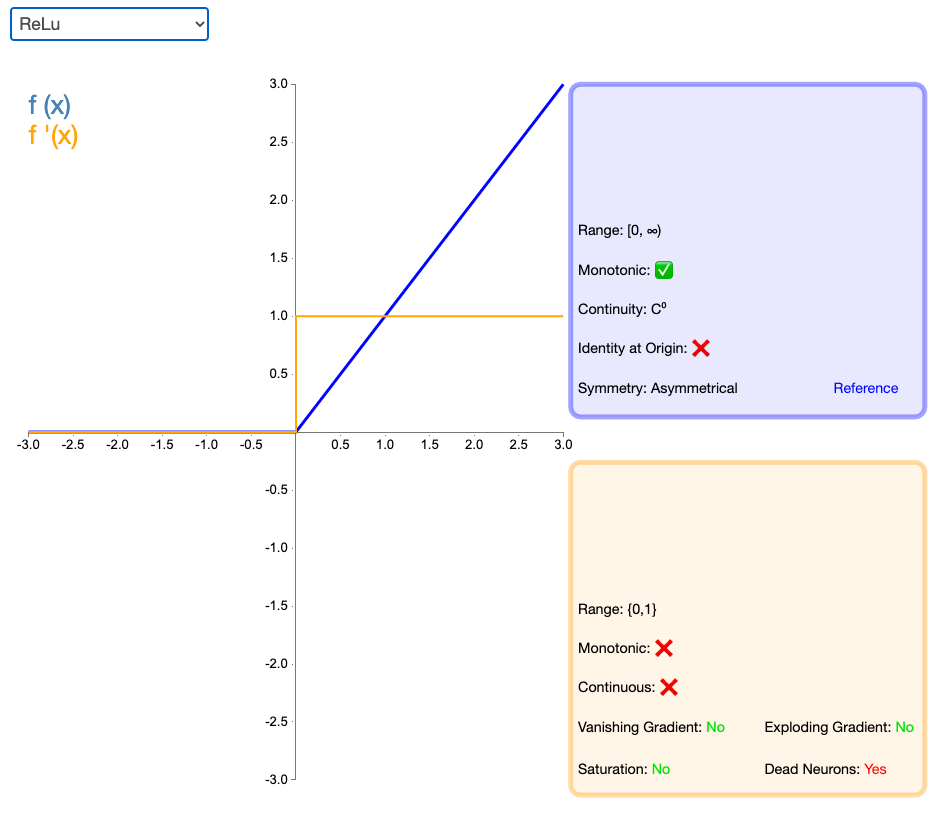
修正线性单元（Rectified linear unit，ReLU）是神经网络中最常用的激活函数。

优点：
1，解决了gradient vanishing （梯度消失）问题（在正区间）
2，计算方便，求导方便，计算速度非常快，只需要判断输入是否大于0
3，收敛速度远远大于 Sigmoid函数和 tanh函数，可以加速网络训练

缺点：

1. 由于负数部分恒为零，会导致一些神经元无法激活
2. 输出不是以0为中心

缺点的致因：

1. 非常不幸的参数初始化，这种情况比较少见
2. learning rate 太高，导致在训练过程中参数更新太大，不幸使网络进入这种状态。

另，ReLU 激活函数在零点不可导，求导按左导数来计算，是0。

2.4 Sigmoid

$$Sig(x)=\frac{1}{1 + e^{-x}}$$ $$Sig'(x)=Sig(x)(1-Sig(x))$$

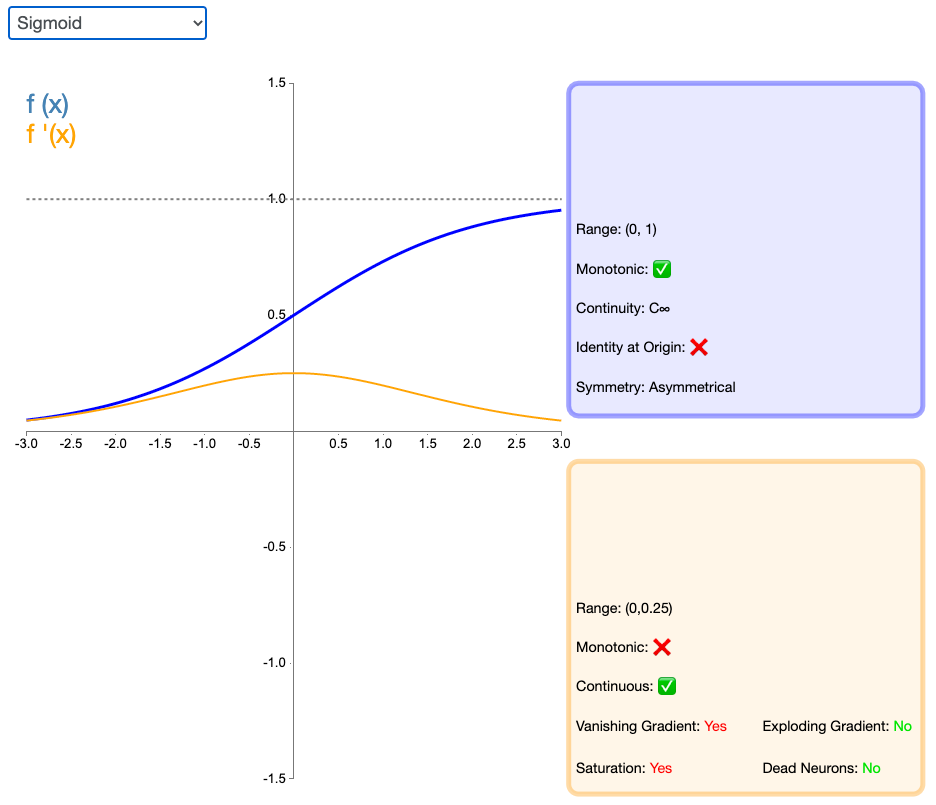
Sigmoid 因其在 logistic 回归中的重要地位而被人熟知，值域在 0 到 1 之间。Logistic Sigmoid（或者按通常的叫法，Sigmoid）激活函数给神经网络引进了概率的概念。它的导数是非零的，并且很容易计算（是其初始输出的函数）。然而，在分类任务中，sigmoid 正逐渐被 Tanh 函数取代作为标准的激活函数，因为后者为奇函数（关于原点对称）。

主要是其有一些缺点：

• 容易出现梯度弥散或者梯度饱和；
• Sigmoid函数的output不是0均值（zero-centered）；
• 对其解析式中含有幂函数，计算机求解时相对比较耗时。

2.5 Tanh

$$tanh(x)=\frac{e^x - e^{-x}}{e^x + e^{-x}}$$ $$tanh'(x)=1-tanh^2(x)$$

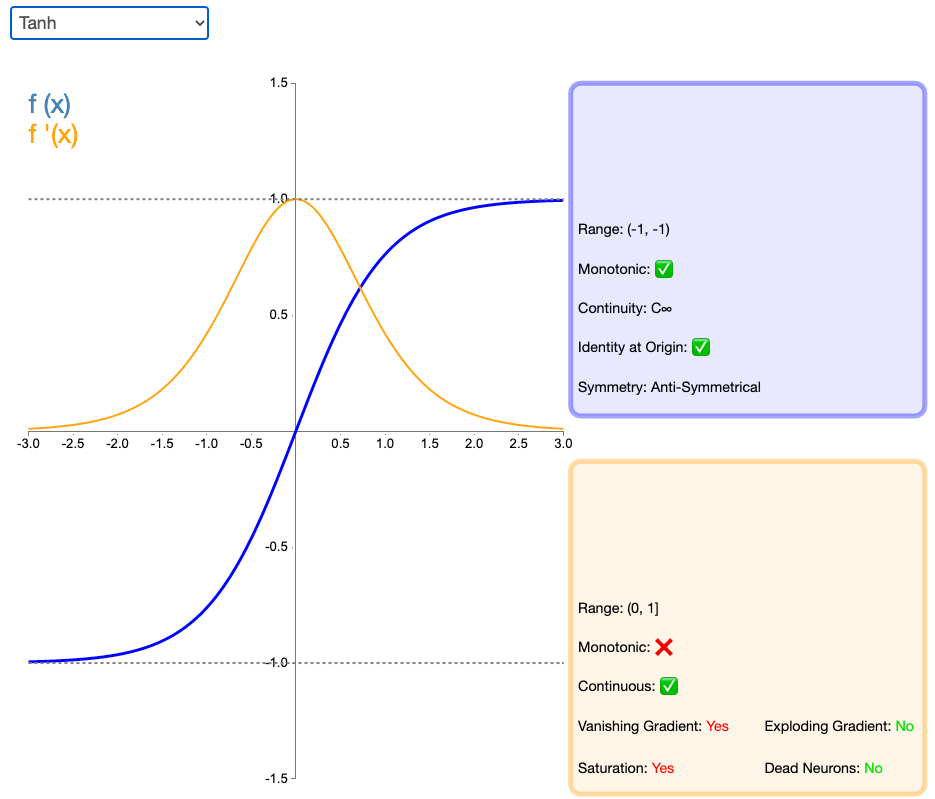
在分类任务中，双曲正切函数（Tanh）逐渐取代 Sigmoid 函数作为标准的激活函数，其具有很多神经网络所钟爱的特征。它是完全可微分的，反对称，对称中心在原点。输出均值是0，使得其收敛速度要比Sigmoid快，减少迭代次数。为了解决学习缓慢和/或梯度消失问题，可以使用这个函数的更加平缓的变体（log-log、softsign、symmetrical sigmoid 等等）.

2.6 Leaky ReLU

$$LeakyReLU(x)= \left\{\begin{matrix} x \quad &for \ x \ge 0 \\ 0.01 x \quad &for \ x < 0 \end{matrix}\right.$$ $$LeakyReLU'(x)= \left\{\begin{matrix} 1 \quad &for \ x \ge 0 \\ 0.01 \quad &for \ x < 0 \end{matrix}\right.$$

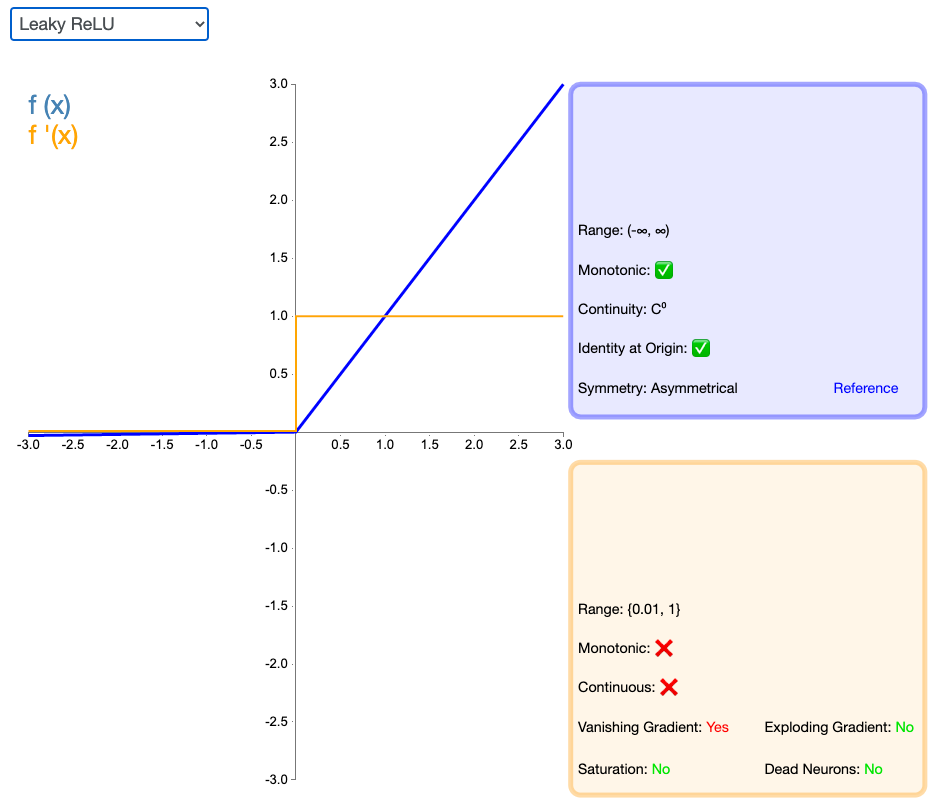
经典（以及广泛使用的）ReLU 激活函数的变体，带泄露修正线性单元（Leaky ReLU）的输出对负值输入有很小的坡度。由于导数总是不为零，这能减少静默神经元的出现，允许基于梯度的学习（虽然会很慢）。

2.7 PReLU

$$PReLU(x)= \left\{\begin{matrix} x \quad for \ x \ge 0 \\ \alpha x \quad for \ x < 0 \end{matrix}\right.$$ $$PReLU'(x)= \left\{\begin{matrix} 1 \quad for \ x \ge 0 \\ \alpha \quad for \ x < 0 \end{matrix}\right.$$

其中$\alpha$一般取根据数据来确定.

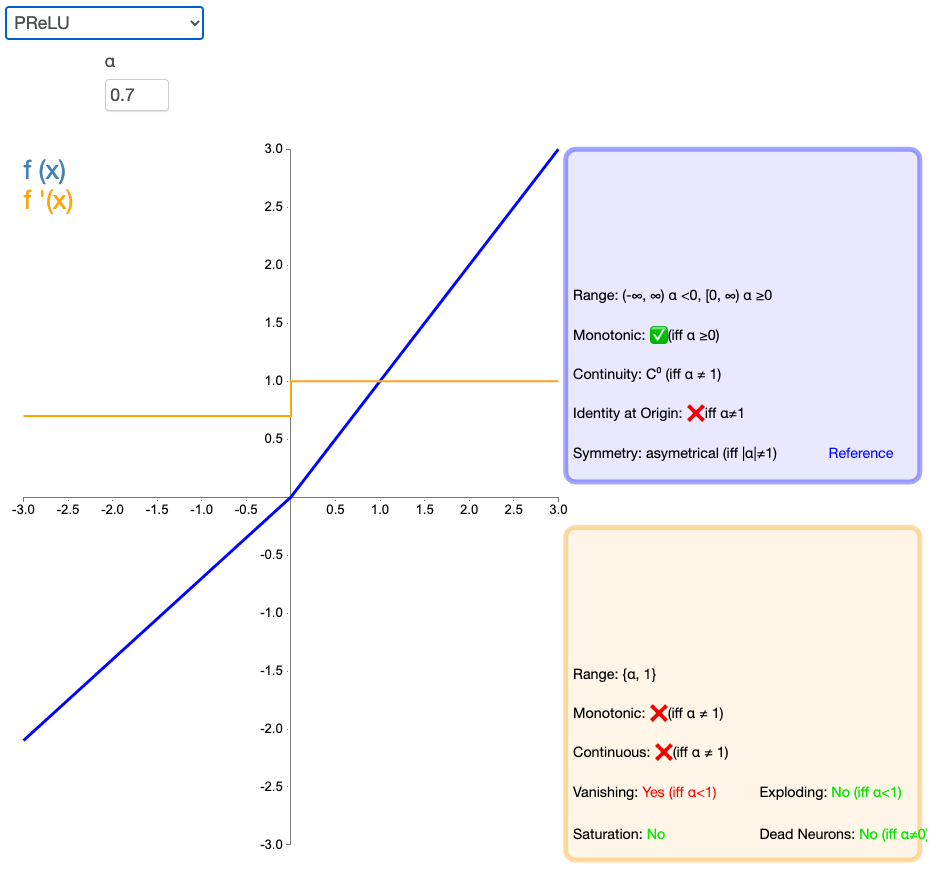
参数化修正线性单元（Parameteric Rectified Linear Unit，PReLU）属于 ReLU 修正类激活函数的一员。它和 RReLU 以及 Leaky ReLU 有一些共同点，即为负值输入添加了一个线性项。而最关键的区别是，这个线性项的斜率实际上是在模型训练中学习到的。如果$\alpha$是一个很小的固定值（如 ai=0.01），则PReLU 退化为 Leaky ReLU（LReLU）。有实验证明：与 ReLU 相比，LReLU 对最终结果几乎没有什么影响。

2.8 RReLU

$$RReLU(x_{ji})= \left\{\begin{matrix} x_{ji} \quad &for \ x_{ji} \ge 0 \\ \alpha_{ji} x_{ji} \quad &for \ x_{ji} < 0 \end{matrix}\right.$$

where

$$\alpha_{ji} \sim U(l,u),l<u \ and \ l,u \in [0,1)$$ $$RReLU'(x)= \left\{\begin{matrix} 1 \quad for \ x \ge 0 \\ \alpha \quad for \ x < 0 \end{matrix}\right.$$

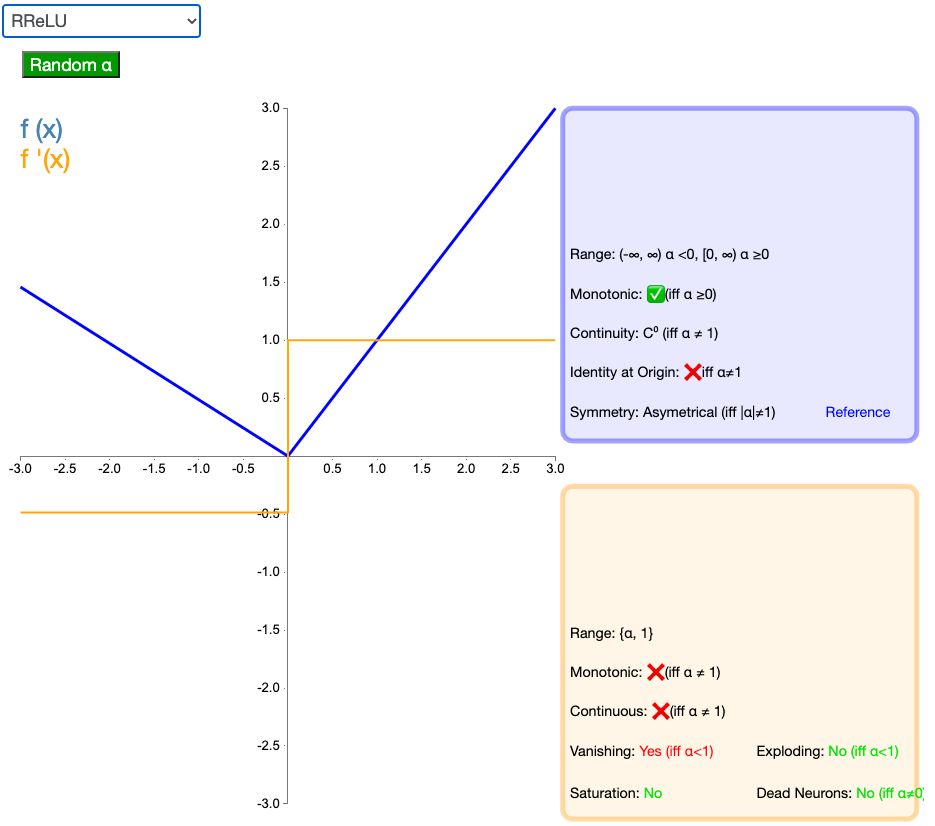
随机带泄露的修正线性单元（Randomized Leaky Rectified Linear Unit，RReLU 也是 Leaky ReLU的一个变体。在 PReLU中，负值的斜率在训练中是随机的，在之后的测试中就变成了固定的了。RReLU 的亮点在于，在训练环节中，aji 是从一个均匀的分布 U(I, u) 中随机抽取的数值。

这里我们要上一个经典的三者对比图：

其中 PReLU 中的 ai 是根据数据变换的；Leaky ReLU中的 ai 是固定的；RReLU中的 aji 是在一个给定的范围内随机抽取的值，这个值在测试环境就会固定下来。

2.9 ELU

$$ELU(x)= \left\{\begin{matrix} x \quad &for \ x \ge 0 \\ \alpha (e^x-1) \quad &for \ x < 0 \end{matrix}\right.$$ $$ELU'(x)= \left\{\begin{matrix} 1 \quad &for \ x \ge 0 \\ \alpha e^x \quad &for \ x < 0 \end{matrix}\right.$$

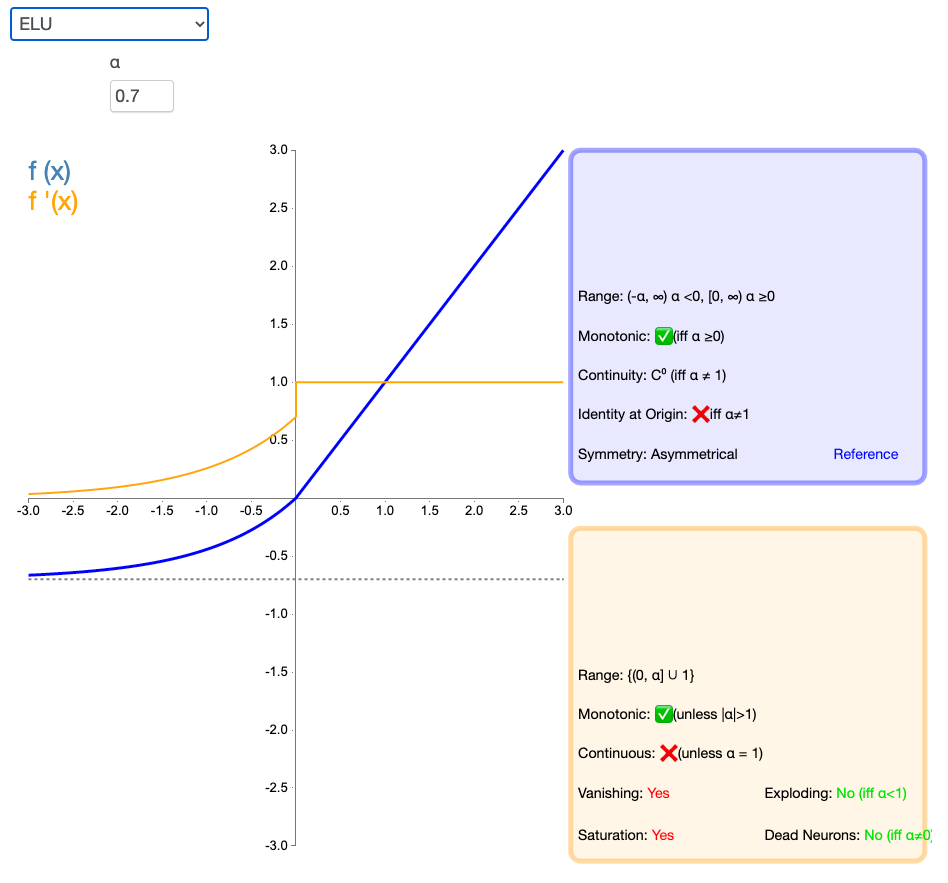
指数线性单元（Exponential Linear Unit，ELU）也属于 ReLU 修正类激活函数的一员。和 PReLU 以及 RReLU 类似，为负值输入添加了一个非零输出。和其它修正类激活函数不同的是，它包括一个负指数项，从而防止静默神经元出现，导数收敛为零，从而提高学习效率。
根据一些研究，ELUs 分类精确度是高于 ReLUs的。ELU在正值区间的值为x本身，这样减轻了梯度弥散问题（x>0区间导数处处为1），这点跟ReLU、Leaky ReLU相似。而在负值区间，ELU在输入取较小值类似于 Leaky ReLU ，理论上虽然好于 ReLU，但是实际使用中目前并没有好的证据 ELU 总是优于 ReLU。时具有软饱和的特性，提升了对噪声的鲁棒性。类似于 Leaky ReLU ，理论上虽然好于 ReLU，但是实际使用中目前并没有好的证据 ELU 总是优于 ReLU。

2.10 SELU

$$SELU(x)=\lambda \left\{\begin{matrix} x \quad &for \ x \ge 0 \\ \alpha (e^x-1) \quad &for \ x < 0 \end{matrix}\right.$$ $$with \lambda=1.0507, \alpha=1.67326$$ $$SELU'(x)= \left\{\begin{matrix} \lambda \quad &for \ x \ge 0 \\ \lambda \alpha e^x \\ =\lambda(SELU(x)+\alpha) \quad &for \ x < 0 \end{matrix}\right.$$

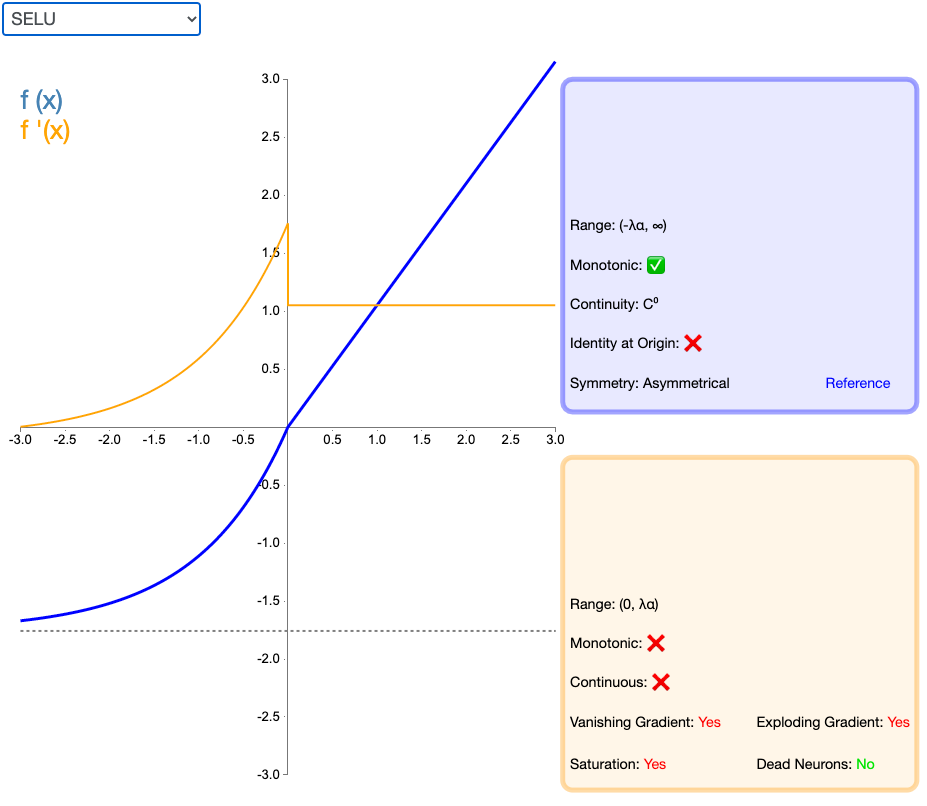
扩展指数线性单元（Scaled Exponential Linear Unit，SELU）是激活函数指数线性单元（ELU）的一个变种。其中λ和α是固定数值（分别为 1.0507 和 1.6726）。这些值背后的推论（零均值/单位方差）构成了自归一化神经网络的基础（SNN）。值看似是乱讲的，实际上是作者推导出来的，详情也可以看作者的github。

2.11 SReLU

$$SReLU(x)= \left\{\begin{matrix} t_l + a_l(x-t_l) &for \ x \le t_l \\ x &for \ t_l < x < t_r \\ t_r + a_r(x - t_r) &for \ x \ge t_r \end{matrix}\right.$$ $$SReLU'(x)= \left\{\begin{matrix} a_l &for \ x \le t_l \\ 1 &for \ t_l < x < t_r \\ a_r &for \ x \ge t_r \end{matrix}\right.$$

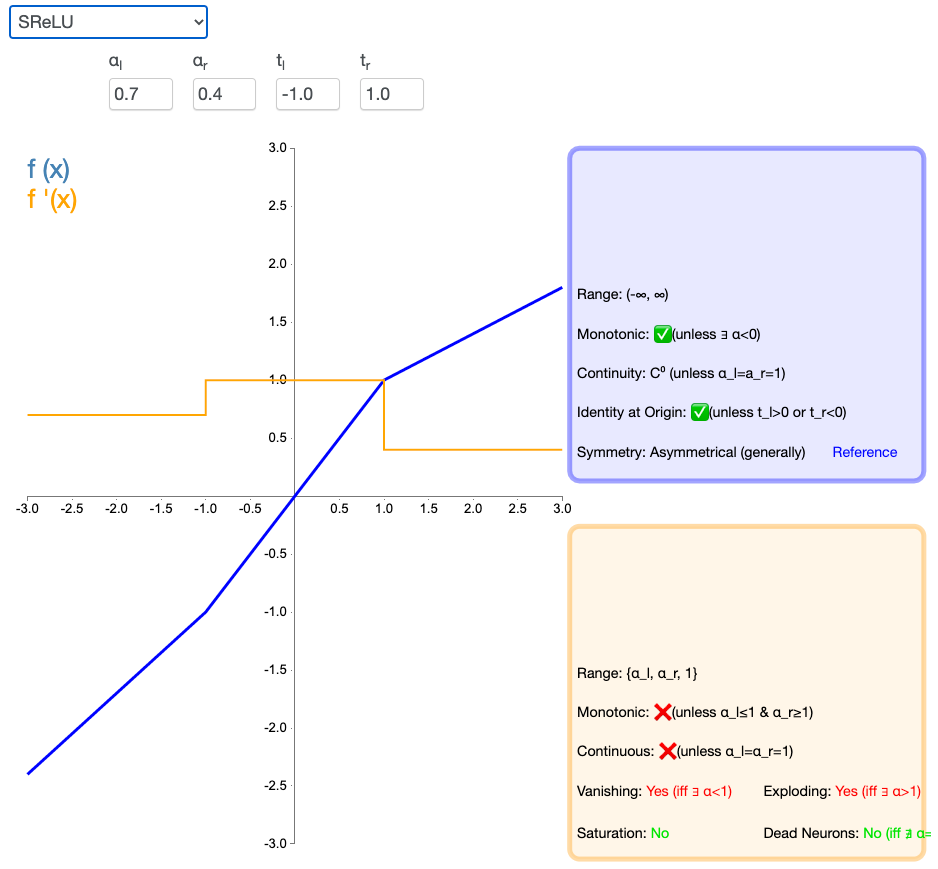
S 型整流线性激活单元（S-shaped Rectified Linear Activation Unit，SReLU）属于以 ReLU 为代表的整流激活函数族。它由三个分段线性函数组成。其中两种函数的斜度，以及函数相交的位置会在模型训练中被学习。

2.12 Hard Sigmoid

$$Hard Sigmoid(x)= max(0, min(1, \frac{x+1}{2}))$$ $$Hard Sigmoid'(x)= \left\{\begin{matrix} 0 &for \ x \le t_l \\ 0.5 &for \ t_l < x < t_r \\ 0 &for \ x \ge t_r \end{matrix}\right.$$

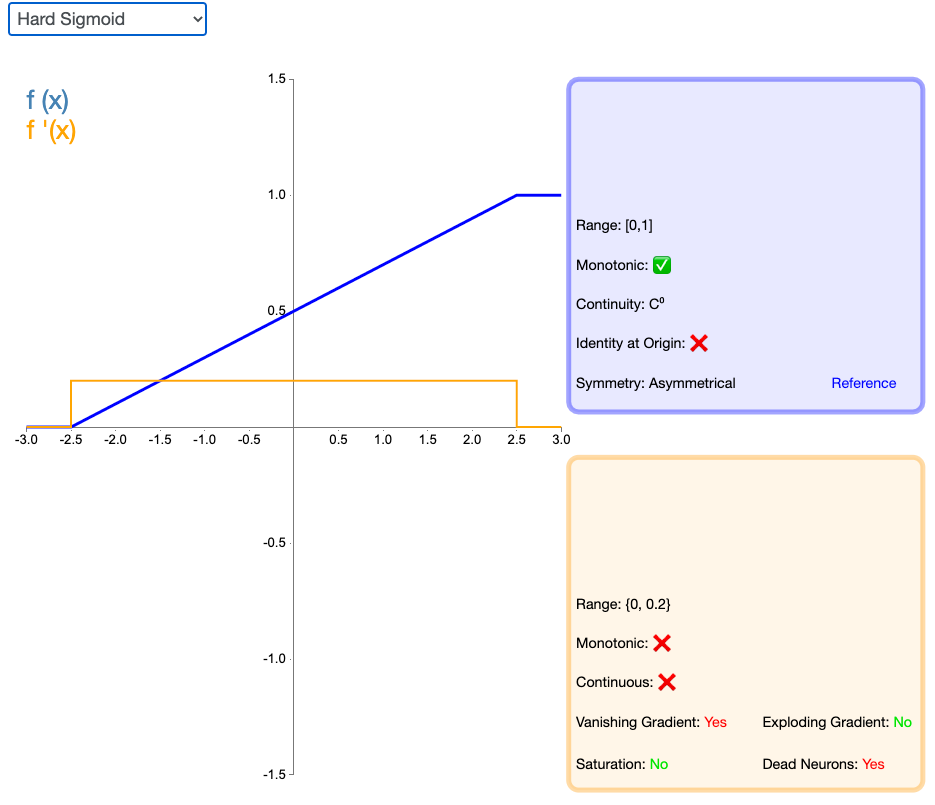
Hard Sigmoid 是 Logistic Sigmoid 激活函数的分段线性近似。它更易计算，这使得学习计算的速度更快，尽管首次派生值为零可能导致静默神经元/过慢的学习速率（详见 ReLU）。

2.13 Hard Tanh

$$Hard Tanh(x)= \left\{\begin{matrix} -1 &for \ x < -1 \\ x &for \ -1 \le x \le 1 \\ 1 &for \ x > 1 \end{matrix}\right.$$ $$Hard Tanh'(x)= \left\{\begin{matrix} 0 &for \ x < -1 \\ 1 &for \ -1 \le x \le 1 \\ 0 &for \ x > 1 \end{matrix}\right.$$

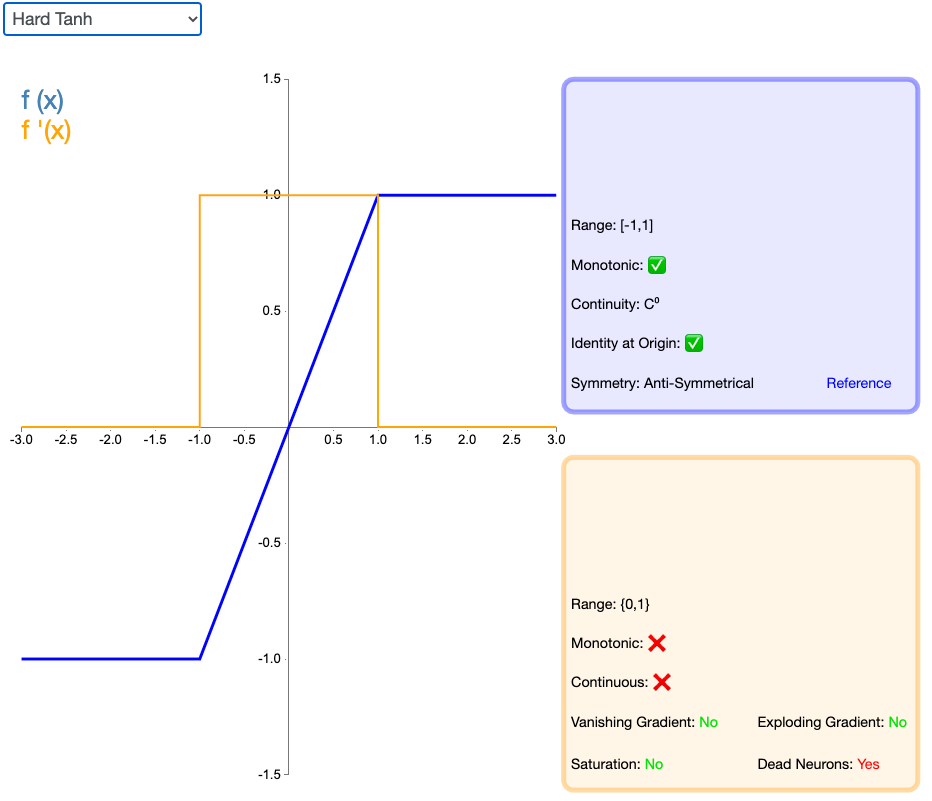
Hard Tanh 是 Tanh 激活函数的线性分段近似。相较而言，它更易计算，这使得学习计算的速度更快，尽管首次派生值为零可能导致静默神经元/过慢的学习速率（详见 ReLU）。

2.14 LeCun Tanh

$$LeCun Tanh(x)=1.7519tanh(\frac{2}{3} x)$$ $$LeCun Tanh'(x)=1.7519 * \frac{2}{3} (1 - tanh^2(\frac{2}{3} x))$$

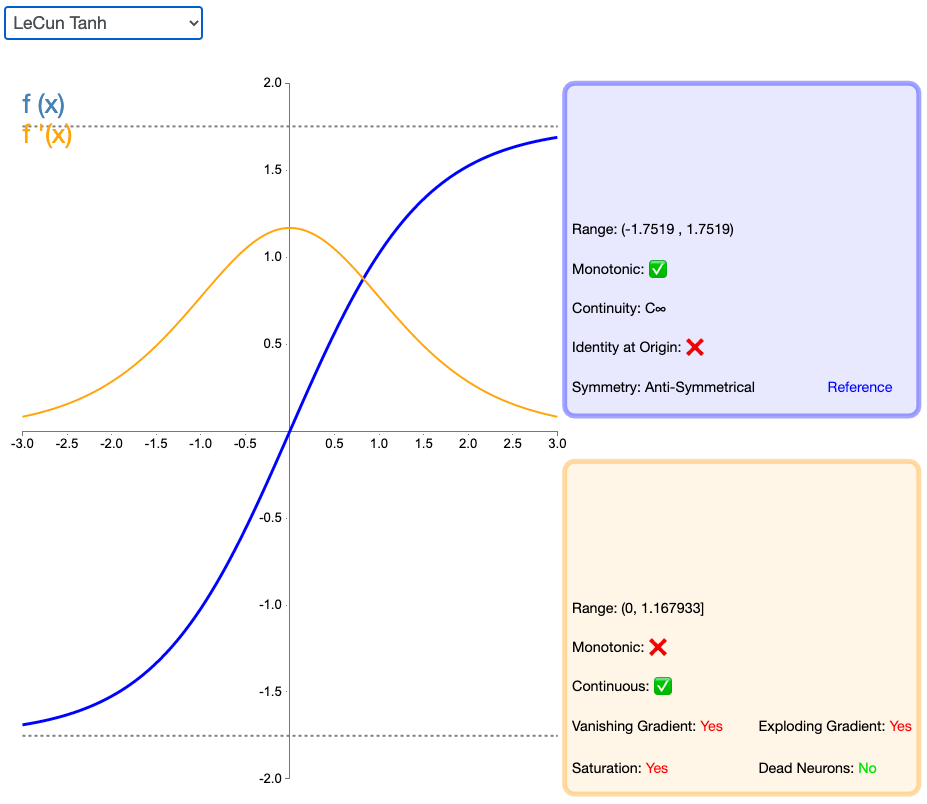
LeCun Tanh（也被称作 Scaled Tanh）是 Tanh 激活函数的扩展版本。它具有以下几个可以改善学习的属性：f(± 1) = ±1；二阶导数在 x=1 最大化；且有效增益接近 1。

2.15 ArcTan

$$ArcTan(x)=tan^{-1}(x)$$ $$ArcTan'(x)=\frac{1}{x^2 + 1}$$

视觉上类似于双曲正切（Tanh）函数，ArcTan 激活函数更加平坦，这让它比其他双曲线更加清晰。在默认情况下，其输出范围在-π/2 和π/2 之间。其导数趋向于零的速度也更慢，这意味着学习的效率更高。但这也意味着，导数的计算比 Tanh 更加昂贵。

2.16 Softsign

$$Softsign(x)=\frac{x}{1 + |x|}$$ $$Softsign'(x)=\frac{1}{(|x| + 1)^2}$$

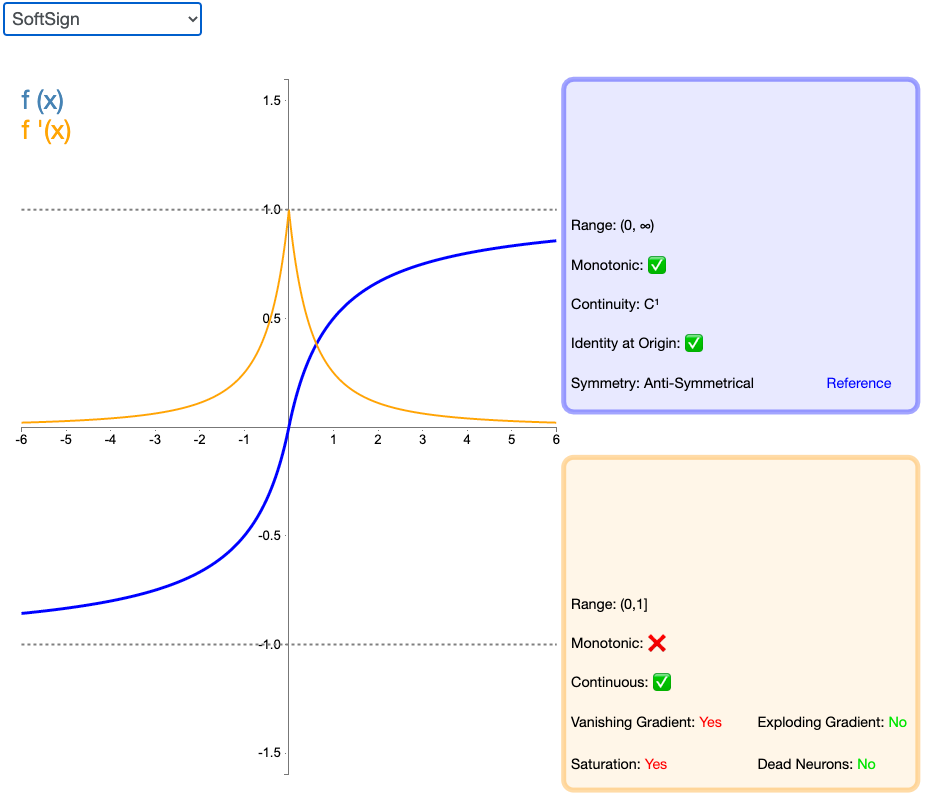
Softsign 是 Tanh 激活函数的另一个替代选择。就像 Tanh 一样，Softsign 是反对称、去中心、可微分，并返回-1 和 1 之间的值。其更平坦的曲线与更慢的下降导数表明它可以更高效地学习。另一方面，导数的计算比 Tanh 更麻烦。

2.17 SoftPlus

$$SoftPlus(x)=ln(1 + e^x)$$ $$SoftPlus'(x)=\frac{1}{1 + e ^{-x}}$$

作为 ReLU 的一个不错的替代选择，SoftPlus 能够返回任何大于 0 的值。与 ReLU 不同，SoftPlus 的导数是连续的、非零的，无处不在，从而防止出现静默神经元。然而，SoftPlus 另一个不同于 ReLU 的地方在于其不对称性，不以零为中心，这兴许会妨碍学习。此外，由于导数常常小于 1，也可能出现梯度消失的问题。

2.18 Signum

$$Signum(x)= \left\{\begin{matrix} 1 &for \ x > 0 \\ -1 &for \ x < 0 \\ 0 &for \ x = 0 \end{matrix}\right.$$ $$Signum'(x)= \left\{\begin{matrix} 0 &for \ x \ne 0 \\ ? &for \ x = 0 \end{matrix}\right.$$

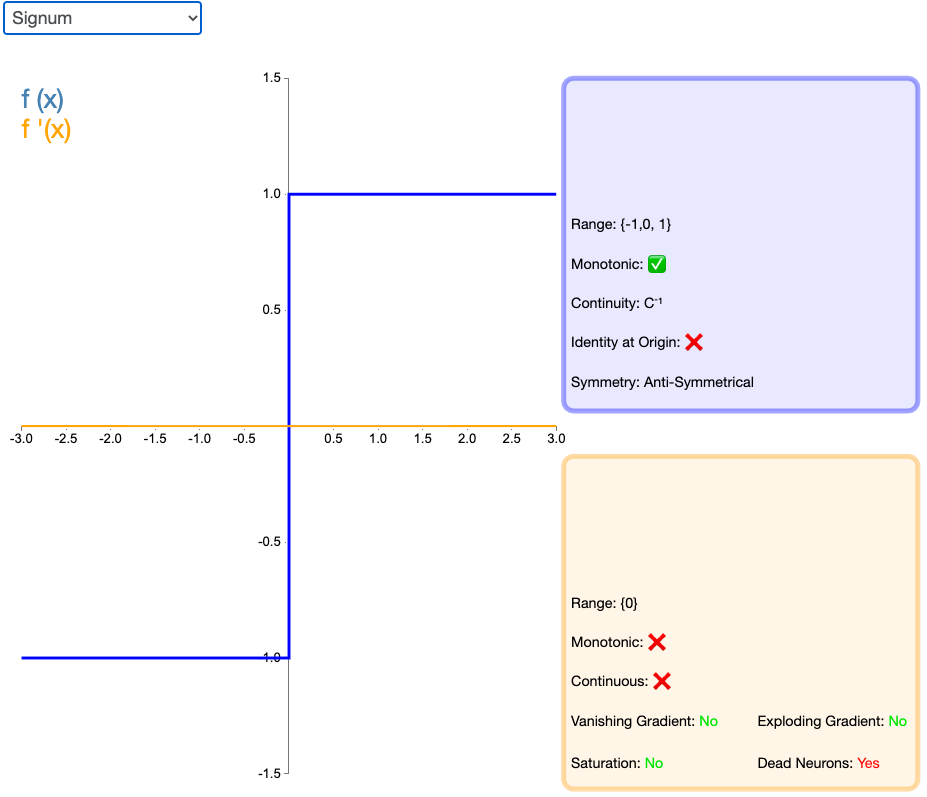
激活函数 Signum（或者简写为 Sign）是二值阶跃激活函数的扩展版本。它的值域为 [-1,1]，原点值是 0。尽管缺少阶跃函数的生物动机，Signum 依然是反对称的，这对激活函数来说是一个有利的特征。

2.19 Bent Identity

$$Bent Identity(x)=\frac{\sqrt{x ^ 2 + 1} - 1}{2} + x$$ $$Bent Identity'(x)=\frac{x}{2 \sqrt{x ^ 2 + 1}} + 1$$

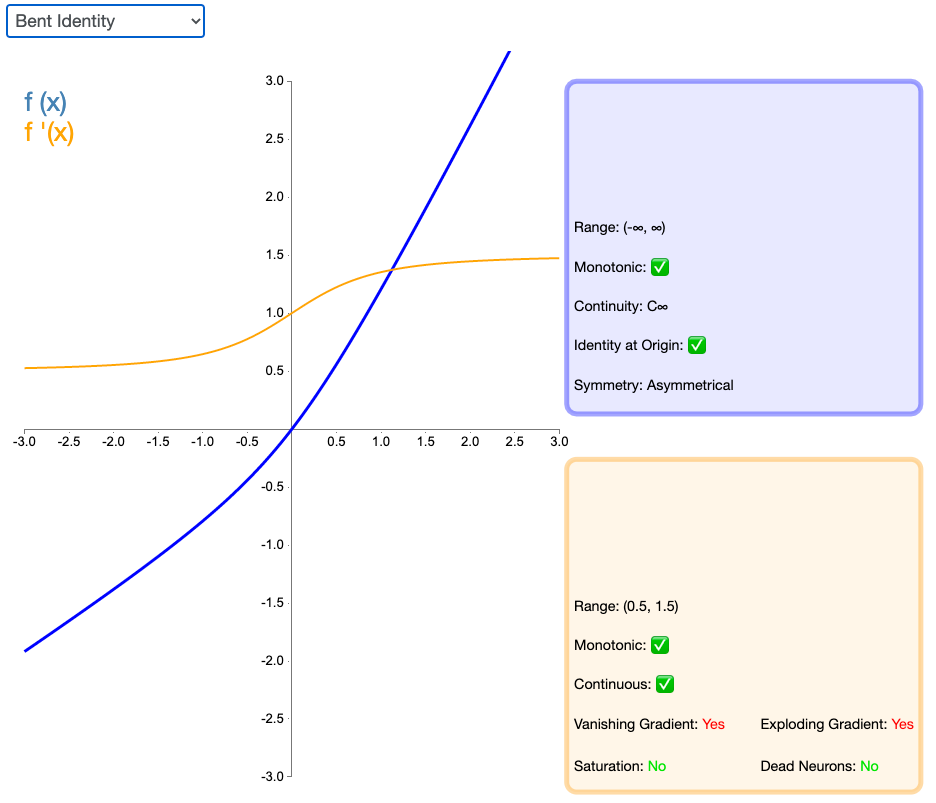
激活函数 Bent Identity 是介于 Identity 与 ReLU 之间的一种折衷选择。它允许非线性行为，尽管其非零导数有效提升了学习并克服了与 ReLU 相关的静默神经元的问题。由于其导数可在 1 的任意一侧返回值，因此它可能容易受到梯度爆炸和消失的影响。

2.20 Symmetrical Sigmoid

$$Symmetrical Sigmoid(x)=tanh(x/2)=\frac{1 - e^{-x}}{1 + e^{-x}}$$ $$Symmetrical Sigmoid'(x)=0.5 (1 - tanh^2(x/2))$$

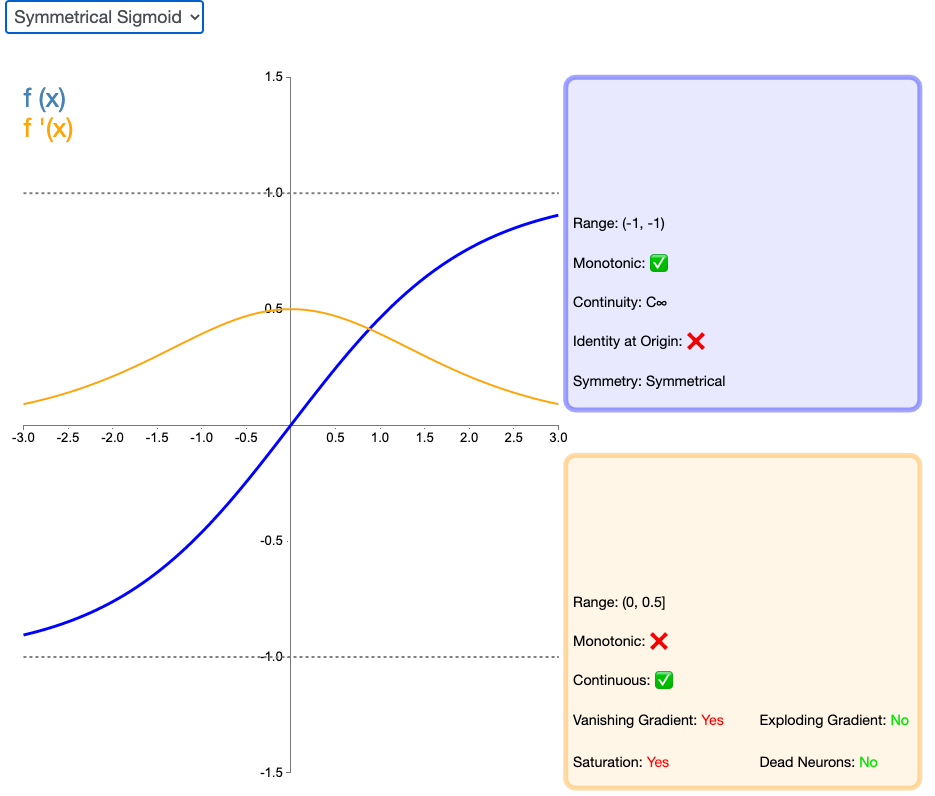
Symmetrical Sigmoid 是另一个 Tanh 激活函数的变种（实际上，它相当于输入减半的 Tanh）。和 Tanh 一样，它是反对称的、零中心、可微分的，值域在 -1 到 1 之间。它更平坦的形状和更慢的下降派生表明它可以更有效地进行学习。

2.21 Log Log

$$Log Log(x)=1 - e^{-e^x}$$ $$Log Log'(x)=e^x(e^{-e^x})=e^{x-e^x}$$

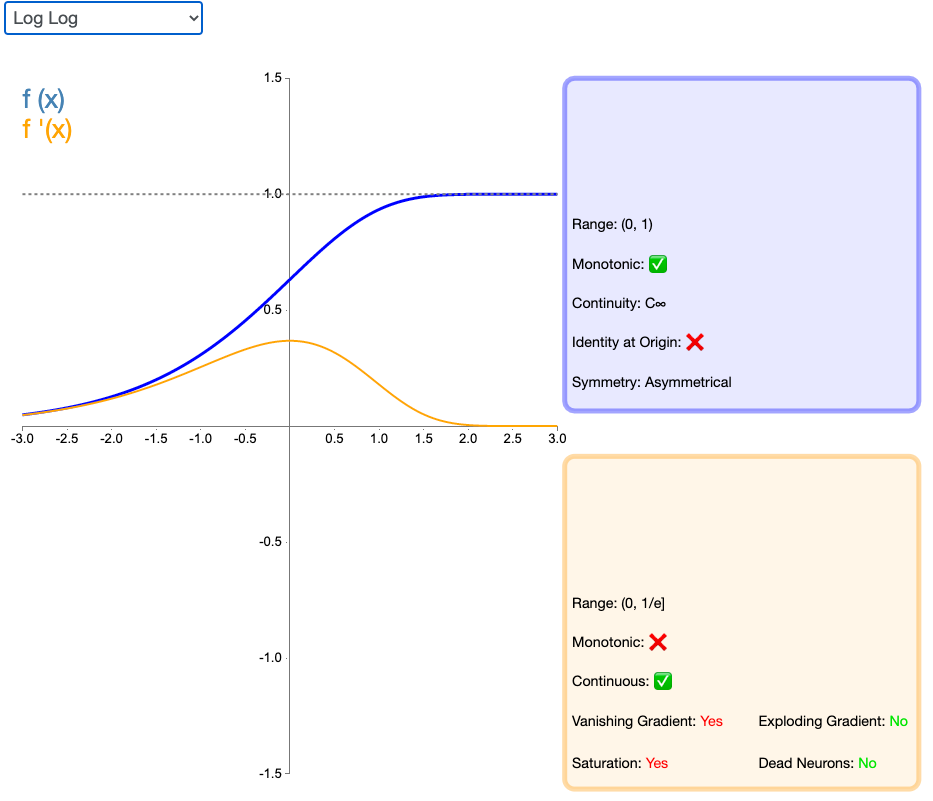
Log Log 激活函数（由上图 f(x) 可知该函数为以 e 为底的嵌套指数函数）的值域为 [0,1]，Complementary Log Log 激活函数有潜力替代经典的 Sigmoid 激活函数。该函数饱和地更快，且零点值要高于 0.5。

2.22 Gaussian

$$Gaussian(x)=e^{-x^2}$$ $$Gaussian'(x)=-2xe^{-x^2}$$

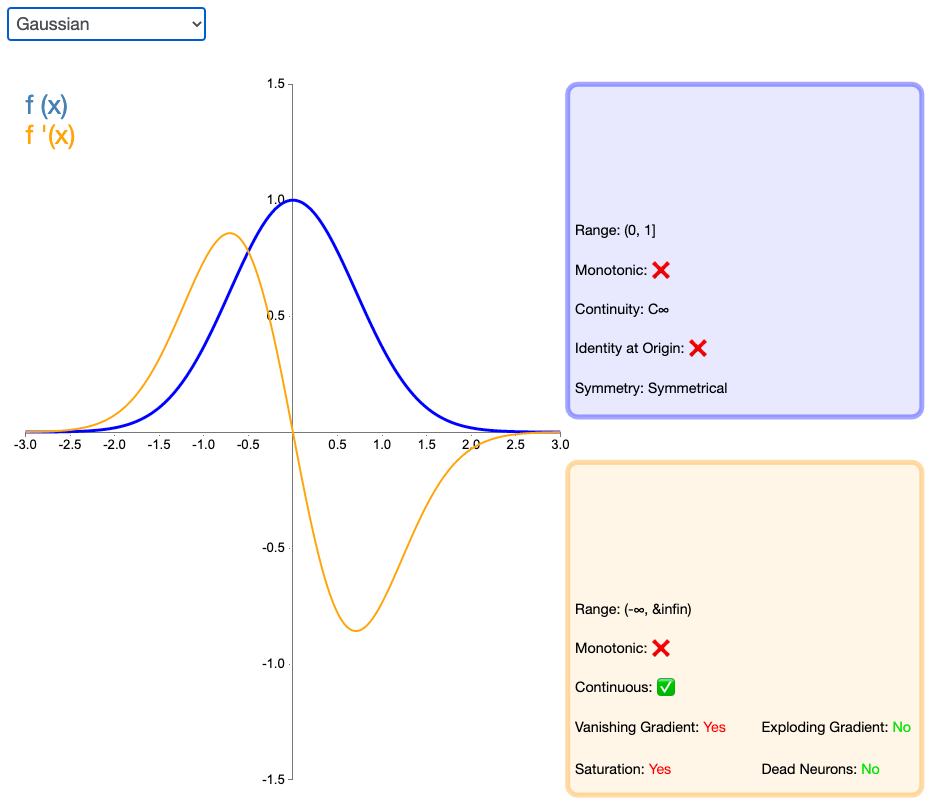
高斯激活函数（Gaussian）并不是径向基函数网络（RBFN）中常用的高斯核函数，高斯激活函数在多层感知机类的模型中并不是很流行。该函数处处可微且为偶函数，但一阶导会很快收敛到零。

2.23 Absolute

$$Absolute(x)=|x|$$ $$Absolute'(x)= \left\{\begin{matrix} -1 &for \ x < 0 \\ ? &for \ x = 0 \\ 1 &for x > 0 \end{matrix}\right.$$

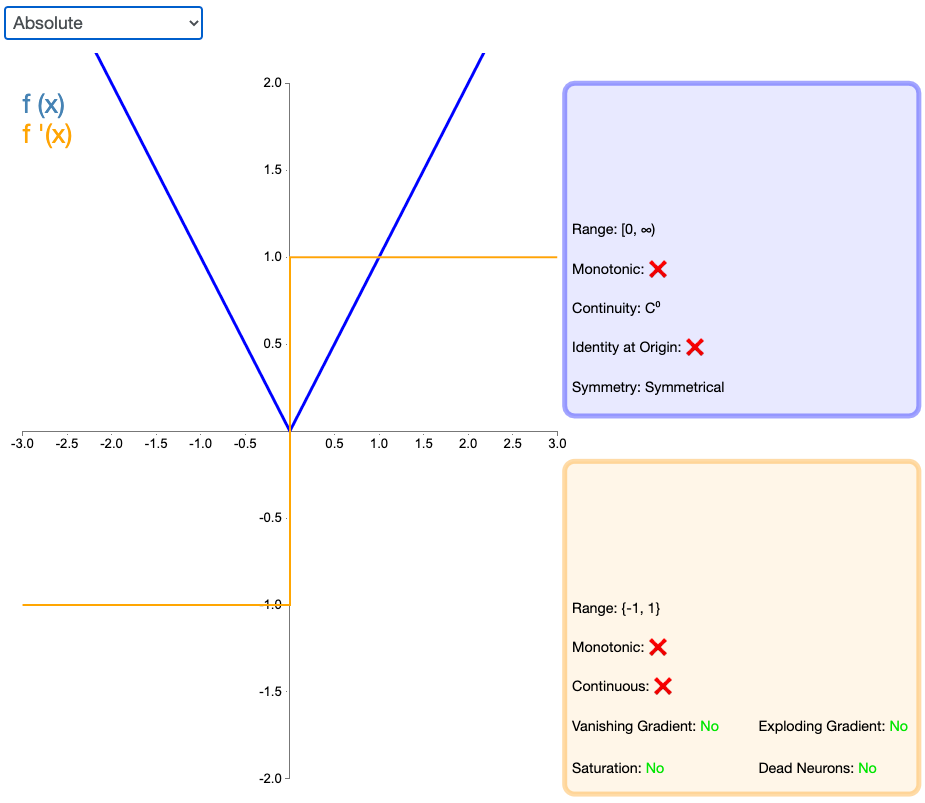
顾名思义，绝对值（Absolute）激活函数返回输入的绝对值。该函数的导数除了零点外处处有定义，且导数的量值处处为 1。这种激活函数一定不会出现梯度爆炸或消失的情况。

2.24 Sinusoid

$$Sinusoid(x)=sin(x)$$ $$Sinusoid'(x)=cos(x)$$

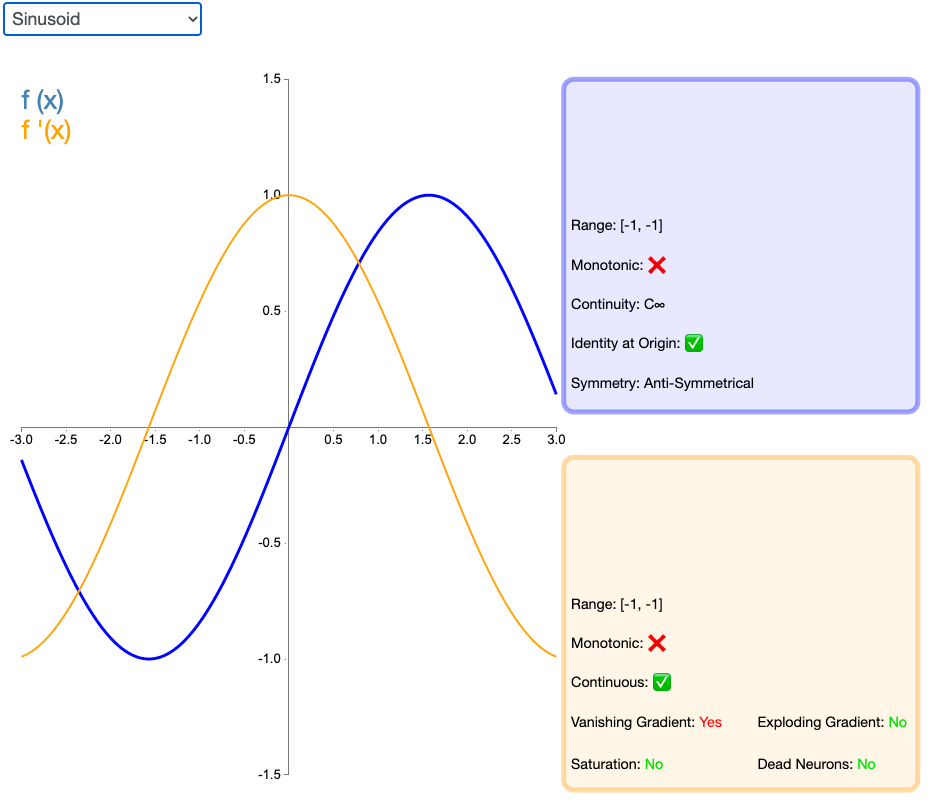
如同余弦函数，Sinusoid（或简单正弦函数）激活函数为神经网络引入了周期性。该函数的值域为 [-1,1]，且导数处处连续。此外，Sinusoid 激活函数为零点对称的奇函数。

2.25 Cos

$$Cos(x)=cos(x)$$ $$Cos'(x)=sin(x)$$

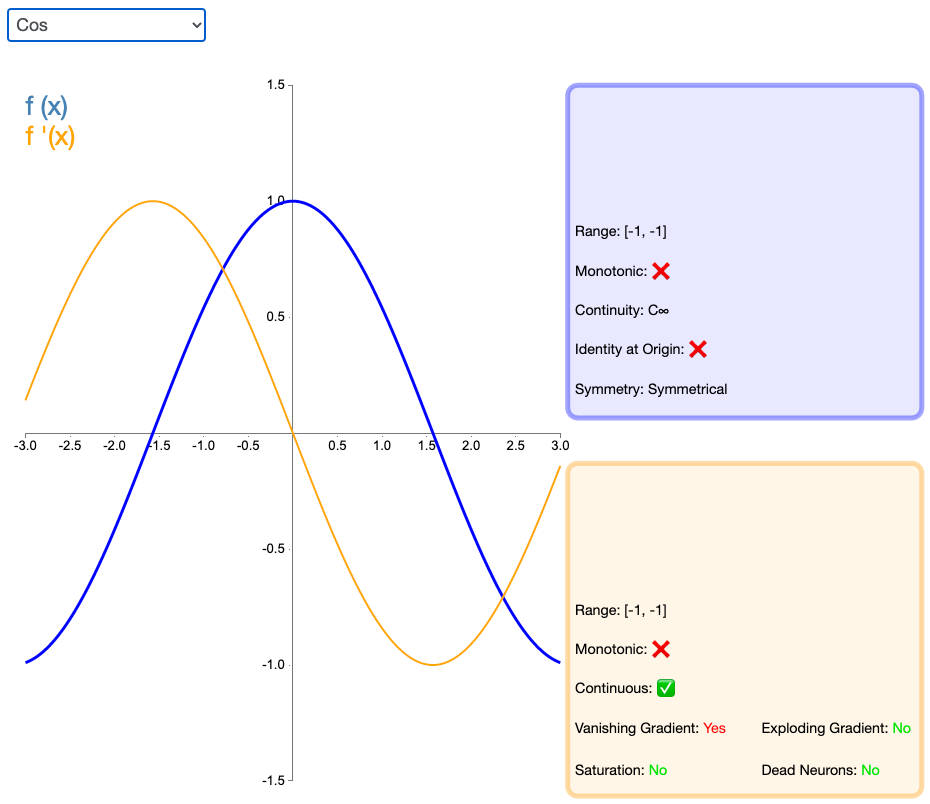
如同正弦函数，余弦激活函数（Cos/Cosine）为神经网络引入了周期性。它的值域为 [-1,1]，且导数处处连续。和 Sinusoid 函数不同，余弦函数为不以零点对称的偶函数。

2.26 Sinc

$$Sinc(x)= \left\{\begin{matrix} 1 &for \ x = 0 \\ \frac{sin(x)}{x} &for x \ne 0 \end{matrix}\right.$$ $$Sinc'(x)= \left\{\begin{matrix} 0 &for \ x = 0 \\ \frac{cos(x)}{x} - \frac{sin(x)}{x^2} &for x \ne 0 \end{matrix}\right.$$

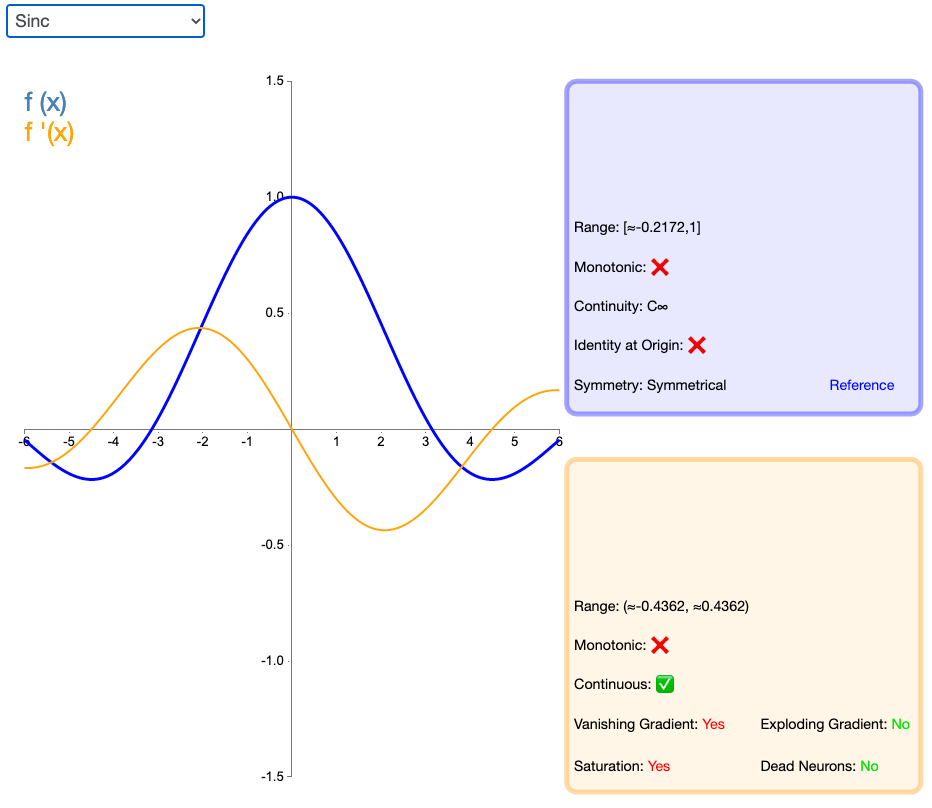
Sinc 函数（全称是 Cardinal Sine）在信号处理中尤为重要，因为它表征了矩形函数的傅立叶变换（Fourier transform）。作为一种激活函数，它的优势在于处处可微和对称的特性，不过它比较容易产生梯度消失的问题。

参考文章
深度学习笔记——常用的激活（激励）函数
Visualising Activation Functions in Neural Networks