22.【其他应用算法】构建一个科学的排行榜体系
为什么要排行榜
排行榜,又名热门榜,听上去似乎是一个很常见的东西,原来它也算是推荐算法的一员?是的,它不但是,并且非常重要,有诸多作用:
- 排行榜可以作为解决新用户冷启动问题的推荐策略。这个不难理解,当一个新用户刚注册时,可以把 近产品中热门的物品推荐给他。
- 排行榜可以作为老用户的兴趣发现方式。即使是老用户,也可以在享受个性化推荐的同时去浏览热门的物品,从中看看哪些感兴趣,哪些不感兴趣,这些行为都是补充或者更新用户兴趣的数据来源。
- 排行榜本身就是一个降级的推荐系统。推荐系统本身是一个软件,因此也会有出现问题的时候,也会有推荐不出来的时候,这个时候考虑到服务的可用性,用排行榜作为一种兜底策略,可以避免推荐位开天窗。
排行榜算法
简单的排行榜,就是直接统计某种指标,按照大小去排序。在社交网站上,按照点赞数、转发数、评论数去排序,这是一种常见、朴素的排行榜。类似的做法还有在电商网站上按照销量去排序。
此类算法不靠谱的原因主要有:
- 非常容易被攻击,也就是被刷榜;
- 马太效应一直存在,除非强制替换,否则一些破了纪录的物品会一直占据在榜单中;
- 不能反映出排行榜随着时间的变化,这一点和马太效应有关。
针对这些弊端,可以设计相应的措施:
1.考虑时间因素
接下来,我要把用户给物品贡献的行为看做是用户在投票,这个很容易理解,好像热门的东西都是大多数人投票民主选举出来的。排行榜中的物品,你可以想象它们每一个都是炙手可热的,都有一定的温度,那么这个温度按照热力学定律来讲,随着时间推移就一定会耗散到周围,温度就会下降。或者,把排行榜想象成一个梯子,每个物品都在奋力往上爬,他们的动力来自用户的手动投票,物品本身都要承受一定的重力,会从梯子上掉下来,用户投票可以抵挡部分重力,投票数不及时或者不够,排行榜上的物品就会掉下来。
把这个规律反映在排行榜分数计算公式中,就比简单统计数量,再强制按照天更新要科学得多。Hacker News 计算帖子的热度就用到了这个思想,它们的做法用公式表达是下面这个样子:
公式中三个字母分别代表如下意义:
- P:得票数,去掉帖子作者自己投票。
- T:帖子距离现在的小时数,加上帖子发布到被转帖至 Hacker News 的平均时长。
- G:帖子热度的重力因子。
其中,重力因子的选择根据情况而定,重力因子越大,帖子的热度衰减越快,不同的重力因子对比如下图所示:
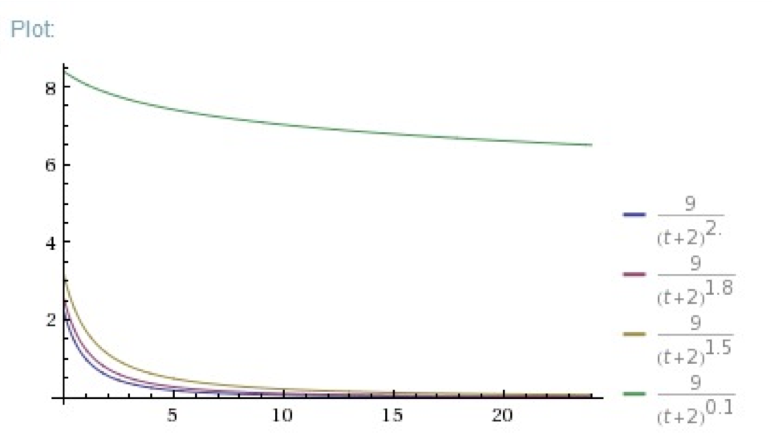
可以看到,重力因子越大,衰减越快。
再看一下,相同重力因子选择的情形下,不同的得票数的对比。
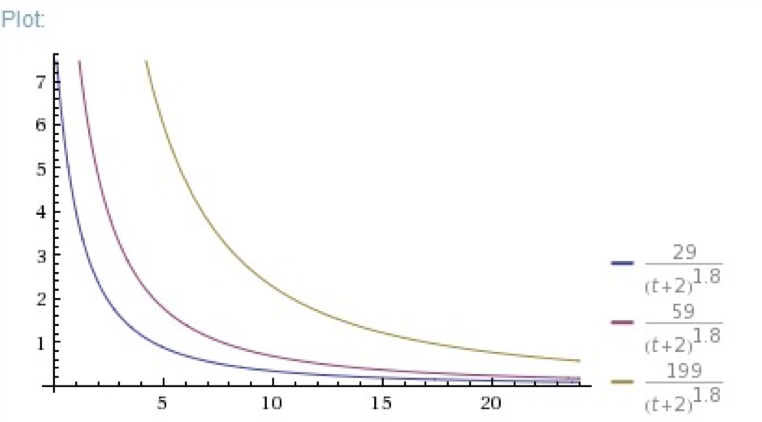
这这个示意图可以看到,这个公式仍然能够反映出相同时间的帖子之间的相对热度差别。
另一个考虑时间因素的排行榜算法是牛顿冷却定律。物品受关注度如同温度一样,不输入能量的话它会自然冷却,而且物体的冷却速度和其当前温度与环境温度之差成正比。将这一定律表述为公式就是下面的样子:
公式中字母的意义如下。
H:为环境维度,可以认为是平均票数,比如电商中的平均销量,由于不影响排序,可以不
使用。
C:为净剩票数,即时刻 t 物品已经得到的票数,也就是那个最朴素的统计量,比如商品的销
量。
t:为物品存在时间,一般以小时为单位。
$\alpha$:是冷却系数,反映物品自然冷却的快慢。
问题来了,这个反映物品自然冷却快慢的 α 该如何确定呢?有一个更直观的办法。假如一个物品在时间过去 B 个单位后,因为增加了 A 个投票数,而保持了热门程度不变,那这样的话 α 应该是多少呢?简单把这个描述列成方程就是下面的样子:
用这个公式加上自己产品的要求来确定 alpha 就容易得多,假如按照 B = 24,也就是过一天来看,来举几个例子:
| 直观解释 | A/C | alpha |
|---|---|---|
| 投票数翻倍 | 1 | 0.03 |
| 投票数增加两倍 | 2 | 0.05 |
| 投票数增加三倍 | 3 | 0.06 |
| 投票数增加三百倍 | 300 | 0.24 |
2. 考虑三种投票
前面的热度计算方法,只考虑用户投票和用户弃权两种,虽然这种情况很常见,但是还有一些产品会存在运行用户投反对票的情形,比如问答网站中对答案的投票,既可以赞成,又可以反对。
在这样的情形下,一般这样来考虑:
- 同样多的总票数,支持赞成票多的,因为这符合平台的长期利益;
- 同样多的赞成票数,支持 有价值的,同样这符合平台长期利益。
以国外某著名程序员问答网站度热门问题的热度计算公式为例:
其中的元素意义如下:
Qviews: 问题的浏览次数。
Ascore:答案的得分。
Qage: 问题发布距离当前的时间。
Qupdated: 问题 后一次修改距离当前的时间。
这个问题热门程度计算方式,也考虑了时间因素。分母反映了问题的陈旧程度,修改问题可以让问题不要衰老过快。分子有三部分构成:
- 左边是问题的浏览量,反映了问题的受关注程度;
- 中间是问题的回答量和问题本身的质量分数的乘积,高质量、回答多的问题占优势;
- 右边是答案的总质量分。
3. 考虑好评的平均程度
前面两种排行榜分数计算法,都是以用户投票的绝对数量作为核心的,那么换个思路来看,从比例来看也是可以的。这也是一些点评网站常常采纳的模式,比如电影点评网站通常会有一个Top250,这也是一种排行榜,以好评比例作为核心来计算排行榜分数。下面来看看这种排行榜。
一个经典的好评率估算公式,叫做威尔逊区间,它这样估算物品的好评率:
实际上,你照着公式中所需的元素去统计就可以计算出排行榜了。我解释一下这个公式中所需的元素,你就可以照着去搬砖了,可以不必理解其中的原理:
- $\hat p$ 就是好评率,比如一百个点评的商品,99 个给了好评,那么这个值就是 0.99
- $z_{1-\frac {\alpha}{2}}$ 是一个置信水平为 alpha Z 统计量,这个查表就可以得到。
威尔逊区间考虑了评价的样本数,样本不足时,置信区间很宽,样本很足时,置信区间很窄。那么这个统计量有哪些应用呢,比如说下面的几个情况。
- 多大比例的人们会采取某种行为?
- 多大比例的人认为这是一个 Spam?
- 多大比例的人认为这是一个“值得推荐的”物品呢?
当你为每一个物品都计算一个威尔逊区间后,你可以采用前面讲到的 Bandit 算法,类似 UCB 的方式取出物品,构建成一个略带变化的排行榜。后,为你呈上某电影点评网站为电影排行榜计算分数的公式,它是另一种对好评率的应用,针对评分类型数据的排行榜:
这个排行榜计算公式,也有一个响当当的名字,叫做“贝叶斯平均”。其中的元素意义描述如下:
R,物品的平均得分,这个很简单,有多少人评分,把他们评分加起来除以人数就是了;
v,参与为这个物品评分的人数;
m,全局平均每个物品的评分人数;
C,全局平均每个物品的平均得分;
别看这个公式简单,它反映了这么几个思想在里面:
- 如果物品没多少人为它投票,也就是评价人数不足,那么 v 就很小,m 就很大,公式左边就很小,右边就很大,于是总分算出来很接近右边部分,也就是接近全局平均分 C;
- 如果物品投票人数很多,那么 v 很大,m 很小,分数就接近它自己的平均分 R。
这个公式的好处是:所有的物品,不论有多少人为它评分,都可以统一地计算出一个合理的平均分数,它已经被国内外电影评分网站采纳在自己的排行榜体系中,当然,它们肯定各自都有根据实际情况的修改。
23.【其他应用算法】实用的加权采样算法
一些场景
想象一个场景:你经过辛辛苦苦抓数据,清洗数据,收集用户行为,目的就是给用户计算兴趣标签。这时候你可能会遇到一个两难的问题:如果给用户计算出兴趣标签的权重了,那应该保留多少标签呢?
这时候,你需要的一个简单的加权采样算法,每次召回时并不使用全部用户标签,而是按照权重采样一部分标签来使用,这样做的好处当然很明显:
- 大大减少召回时的计算复杂度;
- 可以保留更多的用户标签;
- 每次召回计算时还能有所变化;
- 虽然有变化,但是依然受标签的权重相对大小约束。
加权采样的应用不只这一个地方,比如在热门排行榜展示时,也可以用加权采样,而不仅仅按照排行榜分数顺序展示,采用加权采样的展示方法,会让排行榜每次刷新都略有变化,人民群众也会更加喜闻乐见。
加权采样
加权采样有两种情况,一种是能够已知全部样本的个数。这需要遍历整个样本,比如说用户标签采样输出,那么每次采样时仍然需要遍历所有的标签,来依次决定每一个标签输出的概率。另一种是不知道总量样本是多大,或者总量很大,以至于你不愿意全部遍历之后再输出采样结果,这样的数据就是数据流,对应的就是流采样。
1.有限数据集
等概率采样的方法非常简单,任意编程语言中都有伪随机数实现。现在假设你有用户标签若干,每一个标签都有个权重 w,权重高低反映了用户对这个标签的感兴趣程度高低。你希望每次输出一部分标签用于召回推荐候选集,每次输出时都不一样,但是又能反映用户标签的权重,输出的概率和权重成正比。这时候你需要一个公式:
解释一下这个公式:
- $w_i$ 是每个样本的权重,比如用户标签权重;
- R 是遍历每个样本时产生的 0 到 1 之间的随机数;
- $S_i$ 就是每个样本的采样分数
还有另一种加权采样方法,是利用指数分布。
指数分布的参数 $\lambda$,它的倒数,$\frac{1}{\lambda}$就是事件发生时间间隔的期望。把指数分布的这个意义放进标签中来考虑,标签的权重其实反映一个直觉:权重越大的标签,用户消费它就越频繁,也就是间隔时间就会短。
所以根据这个原理,就有另一个加权采样的办法:为每一个标签构造一个指数分布随机数,这个指数分布的参数 Lambda 就是标签权重,然后用这个指数分布的产生一个随机数,再输出随机数最大的 k 个标签作为采样结果。
2. 无限数据集
上面的两种采样都是针对有限数据集的,也就是采样之前都要遍历一遍所有样本。那么如果面对的数据集无限大,或者不知道多大时,该怎么做加权采样呢?这就要讲到另一个采样算法了,名字叫蓄水池采样(也叫蓄水池抽样)。
蓄水池采样可以用在推荐系统的哪些地方呢?比如可以再模型融合之后加一层蓄水池抽样,或者在召回阶段加一层蓄水池采样,这样在不影响整个推荐流程和转化概率的前提下,降低计算复杂度和提升推荐多样性。或者,在线阶段要使用用户的反馈行为做实时推荐,对于不同的用户,活跃程度不同,产生的反馈行为数量不同,你也可以用蓄水池采样,为每个用户取出固定数量的行为用于更新推荐结果。下面,先讲蓄水池采样,再讲加权蓄水池采样。
假如有一个数据集合,一共有 n 条,要从中采样取出 k 个,那么每个样本被选中的概率就是。蓄水池采样的做法是:
- 直接先取出前 k 个样本留着,这 k 个就是随时准备最终要输出的;
- 从第 k+1 个开始,每个都以$\frac{k}{n}$的概率去替换那留着的 k 个样本中的一个。
这个过程,随时可以取用那个 k 个集合作为输出结果,任意时刻,当总样本遍历了 n 个时,他们的概率都是$\frac{k}{n}$ 。这就是蓄水池采样,蓄水池采样,顾名思义,k 个元素的样本集合就是个蓄水池,是任意时刻的采样结果,可以随时取用。
实际上更需要的是加权蓄水池采样。加权蓄水池采样利用的依然是在前面说的第一种加权采样方法,只不过结合了蓄水池采样的思想。要从大数据集中采样 k 个,其具体做法是这样的:
- 为每一个样本生成一个分数,分数还是用这个公式$S_i = R^{\frac {1}{w_i}}$ ;
- 如果结果不足 k 个,直接保存到结果中;
- 如果结果中已经有 k 个了,如果 $S_i$ 比已有的结果里最小那个分数大,就替换它。
24.【其他应用算法】推荐候选池的去重策略
去重是刚需
主要是在两个地方:一个是内容源去重,另一个是不重复给用户推荐。
先说说内容源的去重,这部分以前几年的图文信息流推荐为典型的例子。
如果一个平台自己不生产内容,只是做内容搬运和聚合分发,那么从大量第三方的内容生产处抓取内容,就难免遇到相似甚至重复的内容。这就需要对内容做一个重复检测了。
对内容做重复检测,直观的思路是分词,然后提取关键词,再两两计算词向量之间的距离,距离小于一定阈值后就判定为重复。然而,这对于海量内容,比如几千万以上的内容来说简直就是灾难。其实,内容源去重并不是仅在推荐系统中才首次出现,这早在搜索引擎时代就是一个刚需了,搜索引擎把整个互联网的网页都下载到自己的服务器上,这时,重复冗余的内容就需要被检测出来。
另一个需求是在内容阅读类推荐场景下,给用户推荐的内容不要重复,推荐过的内容就不再出现在推荐候选集中。在你刷一个信息流产品时,不断看到重复的内容,想必不是使用感很好的一件事。因为以抓取作为主要内容来源的信息流产品,不同于社交网站上用户自发产生内容,除非遇到用户恶意发送,否则后者是不容易重复的。
Simhash
内容重复检测,是搜索引擎公司 先遇到的,所以 Google 在 07 年公开了他们内部的内容重复检测算法,这个算法简单有效,甚至造福了今天的信息流推荐产品。
我们直接将原始的内容映射为一个短字符串,这个短字符串就是原始内容的指纹,虽然不是绝对保证和原始内容一一映射,但是不同内容能得到相同指纹的概率非常小。只是这种信息指纹的方法有个非常明显的坏处就是,哪怕原始内容改一个字,得到的信息指纹就会截然不同。此处有点像MD5码一样。
但我们希望的是只要主要内容不变,就算一些不太重要的词句不同,也仍然可以得到相近甚至相同的指纹。这才能更加灵活地进行内容重复检测。是否有这样的算法?有,就是 Simhash。核心思想也是为每个内容生成一个整数表示的指纹,然后用这个指纹去做重复或者相似的检测。下面这个示意图说明了 Simhash 如何把一个原始内容表示成一个整数指纹:
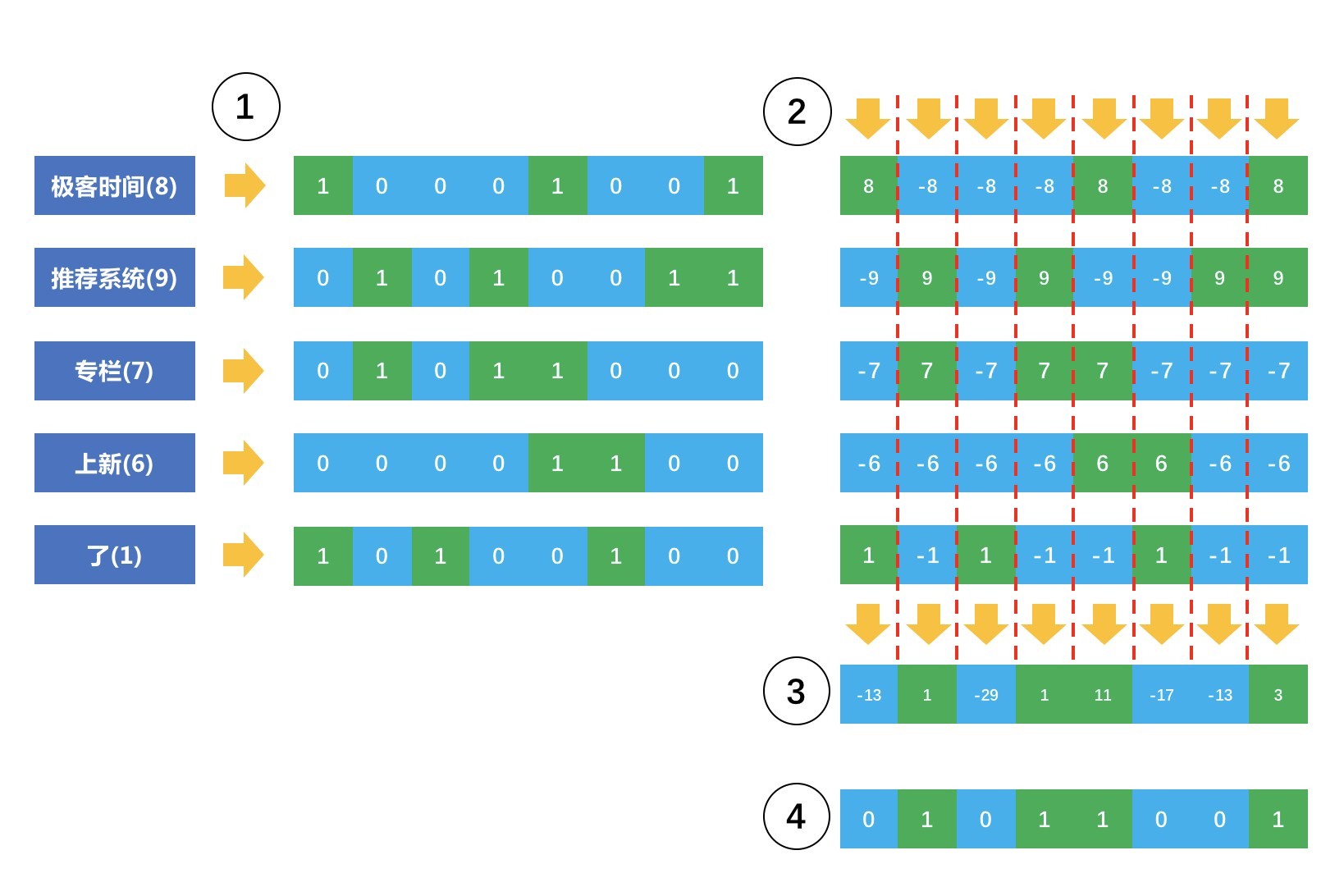
- 首先,对原始内容分词,并且计算每个词的权重;
- 对每个词哈希成一个整数,并且把这个整数对应的二进制序列中的 0 变成 -1,1 还是 1,得到一个 1 和 -1 组成的向量;
- 把每个词哈希后的向量乘以词的权重,得到一个新的加权向量;
- 把每个词的加权向量相加,得到一个最终向量,这个向量中每个元素有正有负;
- 把最终这个向量中元素为正的替换成 1,为负的替换成 0,这个向量变成一个二进制位序列,也就是 终变成了一个整数。
最终这个整数就代表了原始的内容。这个 Simhash 奇妙在哪呢?
看这个示意图中,我故意加了一个不太重要的词“了”,它的权重是 1,对应的加权向量元素不是 1 就是 -1,在上述的第四步中,如果这个词对应的向量缺少了,其实根本不影响最终得到那个整数,因为它很难改变最终向量元素的正负。这就是为什么那些不太重要的词不影响内容之间的重复检测。
Simhash 为每一个内容生成一个整数指纹,其中的关键是把每个词哈希成一个整数,这一步常常采用 Jenkins 算法。
这里简单示意的整数只有 8 个二进制位,实际上可能需要 64 个二进制位的整数,甚至范围更大。得到每个内容的 Simhash 指纹后,可以两两计算汉明距离,比较二进制位不同个数,其实就是计算两个指纹的异或,异或结果中如果包含 3 个以下的 1,则认为两条内容重复。为了高效,也可以直接认为指纹相同才重复,视情况而定。
Bloomfilter
除了内容重复检测,还有一个需求是防止已经推荐的内容被重复推荐。这个刚需和上述内容重复相比, 大的不同就是过滤对象不同,上述 Simhash 过滤对象是内容本身,而这里则一般是内容的 ID。
内容的 ID 一般是用一个 UUID 表示,是一个不太长的字符串或者整数。对于这类形如模式串的去重,显然可以用单独专门的数据库来保存,为了高效,甚至可以为它建上索引。但对于用户量巨大的情况下,这个做法对存储的消耗则不可小看。实际上,解决这类看一个字符串在不在一个集合中的问题,有一个有点老但很好用的做法,就是 Bloomfilter,有时候也被称为布隆过滤器。
布隆过滤器的原理也要用到哈希函数。它包含两部分:一个很长的二进制位向量,和一系列哈希函数。
Bloomfilter 是一个很巧妙的设计,它先把原始要查询的集合映射到一个长度为 m 的二进制位向量上去,它映射的方法是:
- 设计 n 个互相独立的哈希函数,准备一个长度为 m 的二进制向量,最开始全是 0;
- 每个哈希函数把集合内的元素映射为一个不超过 m 的正整数 k,m 就是二进制向量的长度;
- 把这个二进制向量中的第 k 个位置设置为 1;也就是一个元素会在二进制向量中对应 n 个位置为 1。
示意图如下:
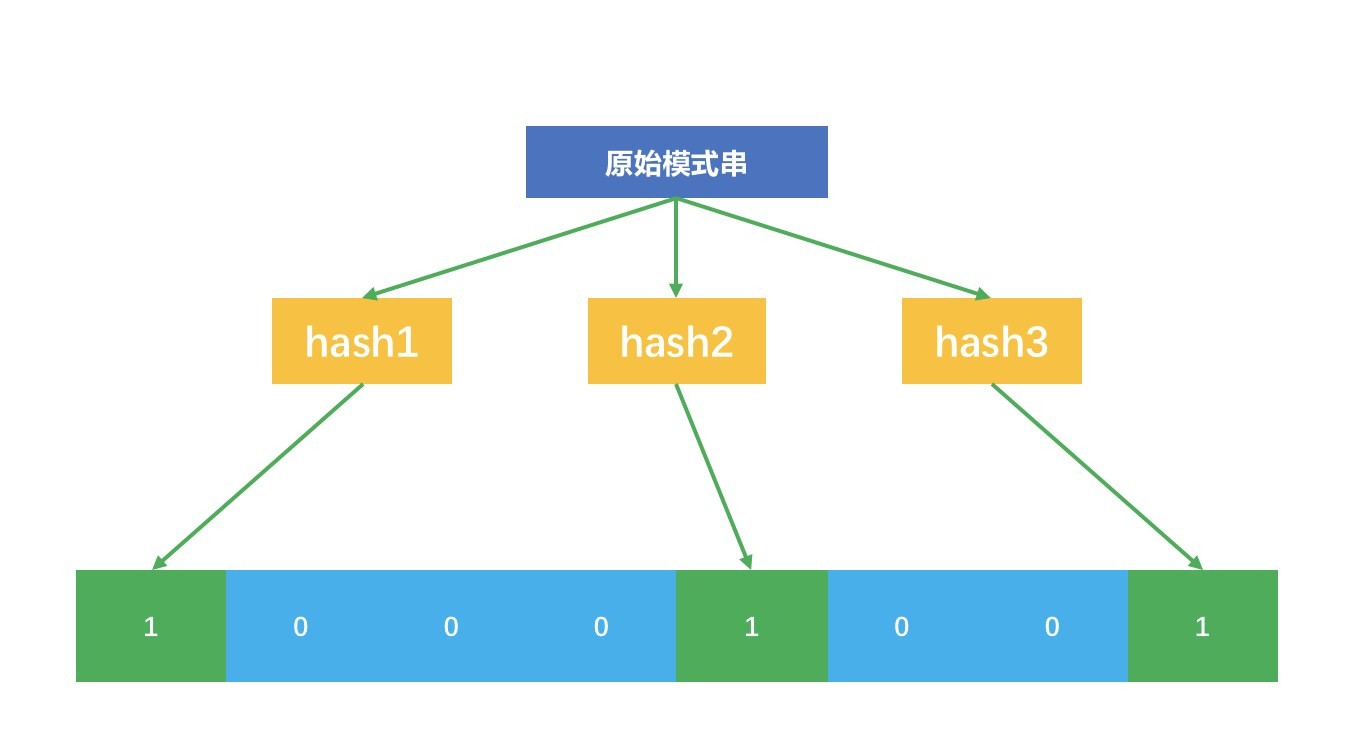
这个示意图中,原始的模式串经过三个互相独立的哈希函数,映射到 8 位二进制向量中的三个位置了。原始的模式串集合经过这样的处理后,就得到一个很大的二进制向量。在应用阶段时,假如来了一个模式串 s,需要查询是否在这个集合中,也需要经过同样的上述步骤。每个哈希函数对这个模式串 s 哈希后都得到一个整数,看看这个整数在二进制向量中所指示的位置是不是 1,如果每个哈希函数所指示的位置都是 1,就说明模式串 s 已经在集合中了。
需要说明的是,Bloomfilter 也并不是百分之百保证的,有很小的概率把原本不存在集合中的模式串判断为存在。这样就会造成那些明明还没有推荐给用户的内容 ID 就再也不会推荐给用户了,当然,这个小概率是可以承受的。
总结
在推荐系统中,虽然我们十分关心推荐匹配的效果,但是别忘了,对原始内容的挖掘和清洗往往更加重要。这其中就包括对重复内容的检测。两种去重策略都是牺牲一点误伤的概率换得大幅度的效率提升,具体的做法都是要借助哈希函数。只是哈希函数的结果在两个算法中有不同的处理手段,Simhash 是加权,Bloomfilter 则是用来做寻址。
精选留言:
Counting Bloom Filter支持删除操作,除了已有的二进制向量,向量的每一位对应一个整数计数器。每当增加一个元素时,哈希函数映射到的二进制向量对应的整数计数器加一,删除时减一。有了这个操作可以增加,查找和删除集合里的元素。
业界一般是不对布隆过滤器剔除元素,原因是剔除已有元素有可能导致整体数据错误。想到一种方法:使用一个同样长度的向量,记录对于位置1的个数,剔除是先hash6映射,对于1的位置,个数大于的话不变,等于1的话设为0;不过,缺点是这个向量占空间,存储成稀疏向量吧
