从 MMOE 到 PLE 模型

1 引言

在当下以深度学习为基调的推荐系统中，传统的单目标优化往往会带来一些不健康的生态指标变化，例如仅优化 CTR 可能会使得用户深层行为下降，往往推出一些博眼球和标题党等内容或商品。所以就催生了利用模型对 CLICK 后的各种深层行为的学习，最常用的便是 CVR（转化率），当然还有 cfr（收藏率）以及 viewtime（浏览时长）等等目标，视具体场景的业务指标而定。

为了解决上述问题，最原始的方法便是多模型多分数融合，也即对不同目标单独构建模型，线上独立打分进行融合，但是这样带来的问题便是深度行为的样本一般不足，难以使得模型学习的很好，而且独立建模成本高昂。为了进一步提效，目前主流的方法便是统一模型进行不同目标的联合训练，而模型内部不同任务之间存在一定信息共享。如此，

• 一方面使得相关任务之间能够互相分享和补充信息，促进各任务学习能力；
• 另一方面，梯度在反向传播的时候，能够兼顾多个任务模式，提高模型的泛化能力。

多任务学习模型有很多种，例如阿里的 ESSM 模型，谷歌的 MMOE 模型，包括本文重点介绍的 CGC 和 PLE 模型，来自由腾讯团队发表的获得 RecSys2020 最佳长论文奖得文章：Progressive Layered Extraction (PLE): A Novel Multi-Task Learning (MTL) Model for Personalized Recommendations。当然还有很多其他变种的多任务模型，而在接下来得内容将聚焦介绍模型结构得迭代变化。

2 目标

实践中上述的理想目标往往会不及预期，主要原因在于, 当任务之间相关性较高的时候，能够一定程度通过信息共享来促进模型的学习效率，但不太相关时会产生负迁移（negative transfer），即网络表现变差。前面提到谷歌提出的MMOE模型就是为了缓解负迁移现象。但，另一方面，工业实践中往往还面临一个普遍的问题，那就是跷跷板现象（seesaw phenomenon）。也就是在多任务联合训练中，往往部分任务能够相对于独立训练获得提升，但同时伴随着其他个别任务效果下降。

本人在实际工作中也遇到了上述问题，跷跷板现象是比较明显的结果导向，例如 cfr（收藏率）提升了，但 ctr（点击率）下降了。而对于负迁移问题，比较好验证其触因，可以直接计算样本中不同任务 label 之间的相关性。以博主自己的一个实际工作场景为例：

在某电商瀑布流的推荐中，样本中核心 label 有 ctr（点击）、ccr（查看细分sku）、cfr(收藏)、cvr（下单）。当然不仅限于这些，对于场景核心 label 的选取主要取决于业务目标和 label 的覆盖度。部分同学在实际中可能会认为行为之间应该具有较强的相关性，然而实际上结果可能大相径庭。如下表所示是实际样本的一个统计结果（大约一天几亿量级的数据），可以发现在渗透漏斗链路上，离 ctr 越远的行为相关性越低。

本文介绍的从 MMOE 迭代到 PLE 的模型，其提出者目的正是为了缓解上述问题。PLE 模型也是被部署在了腾讯的视频推荐系统中，其线上多目标分数融合方式如下：

$$\begin{array}{r} score = pVTR^{w_{VTR}} \times pVCR^{w_{VCR}} \times pSHR^{w_{SHR}} \times \dots \times pCMR^{w_{CMR}} \times f(video\_len) \end{array}$$

其中，公式中每一项右上角的 $w$ 都是权重超参数。video_len 表示视频的原始时长，其有一个映射函数 $f$，是一个 non-linear 函数，可取 sigmoid 或者 log 函数。模型结构如下所示：

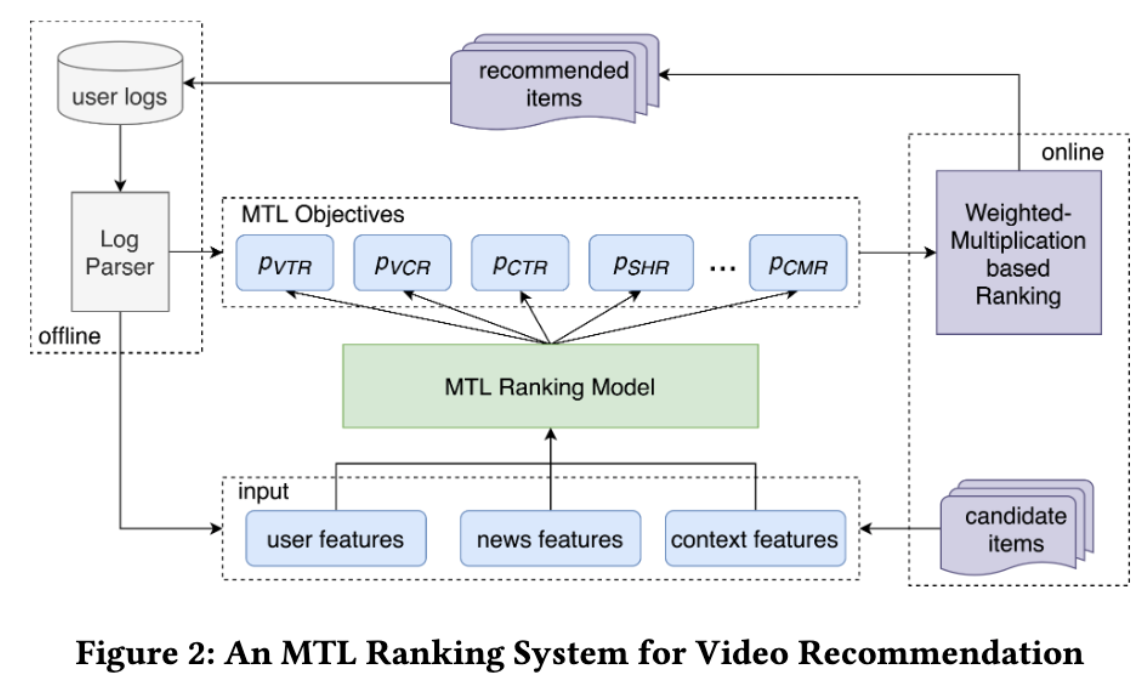
在这里，VCR (View Completion Rate)和VTR (View-Through-Rate)是最重要的2个指标。VCR 是指视频完成度，例如1min的视频看了0.5min，便有VCR=0.5。以此作为 Label 可以构建一个回归问题，以 MSE 作为评估指标。VTR 则是指是否是一次有效观看，这一般可以构建成一个二分类模型，AUC 作为评估目标。

值得注意的是，此Label的打标签一般因业务场景不同而有所区别:

• 需要通过列表主动点击到落地详情页的时候，一般 VTR 对应的 Label 就是用户是否主动点击；
• 如果是单列自动播放的视频流的时候，就会存在视频的默认播放问题，需要进行一定的阈值截断来进行 Label 的打标签；

如上所述，实际上两个任务的关系很复杂。以腾讯实际场景为例，VTR是播放动作和VCR的耦合结果，因为在有wifi下，部分场景有自动播放机制，播放率相对就较高，就需要设定有效播放时长的阈值。没有自动播放机制时候，相对更为简单，且播放率会较低。

如上图所示，是其团队对比了一些主流 MTL 模型在 VCR 和 VTR 任务上相对单任务模型的离线对比结果。从图中可以看到，大多 MTL 模型都是一个任务好于单任务模型另一个则较差，这便是前文提到的跷跷板现象（seesaw phenomenon）。以MMOE为例，其在 VTR 上有一定收益，但是在 VCR 上几乎无收益。核心原因在于，其 Experts 是被所有任务共享，会有噪声，且他们之间没有交互，联合训练有折扣。

而该团队提出的 PLE 模型在实验对比中最好，其线上实验也取得了2.23%的view-count和1.84%的阅读时长提升效果。我们可以先将其核心优化点总结成如下：

• 解耦 Experts 网络，改进了模型结构；
• 优化了多目标 loss 融合的方法，提高了训练的效率；

3 MMOE

前文提到很多与MMOE(Multi-gate Mixture-of-Experts)模型的对比，咱们先来回顾一下该模型的结构。

如上图所示，该模型实际上是在多个 Expert 基础上，对每一个任务的 Tower 都构建一个 Gate 网络。整个模型可以用数理表达式：

\begin{array}{l} 
f^k(x)=\sum_{i=1}^n g^k(x)_{i} f_{i}(x)
\\
g^k(x)=Softmax(W_{gk}x)
\end{array} 

其中，$g^k$ 表示第 k 个任务中的用来控制 experts 结果的门控网络。

该网络的目的是使得每个 Task 通过自己独立的 Gate 网络来学习不同的 Experts 网络的组合模式。模型的 loss 一般是各个任务的 loss 加和，如果其中某个任务的 loss 占比过高，则梯度主要沿着其下降的方向更新，有可能降低其他任务的精度。

4 CGC

这里介绍的CGC（Customized Gate Control）模型是一种单层多任务网络结构，它是本文介绍的最终版本PLE模型的简单版本或者说其组成部分。下面展示的是其网络结构：

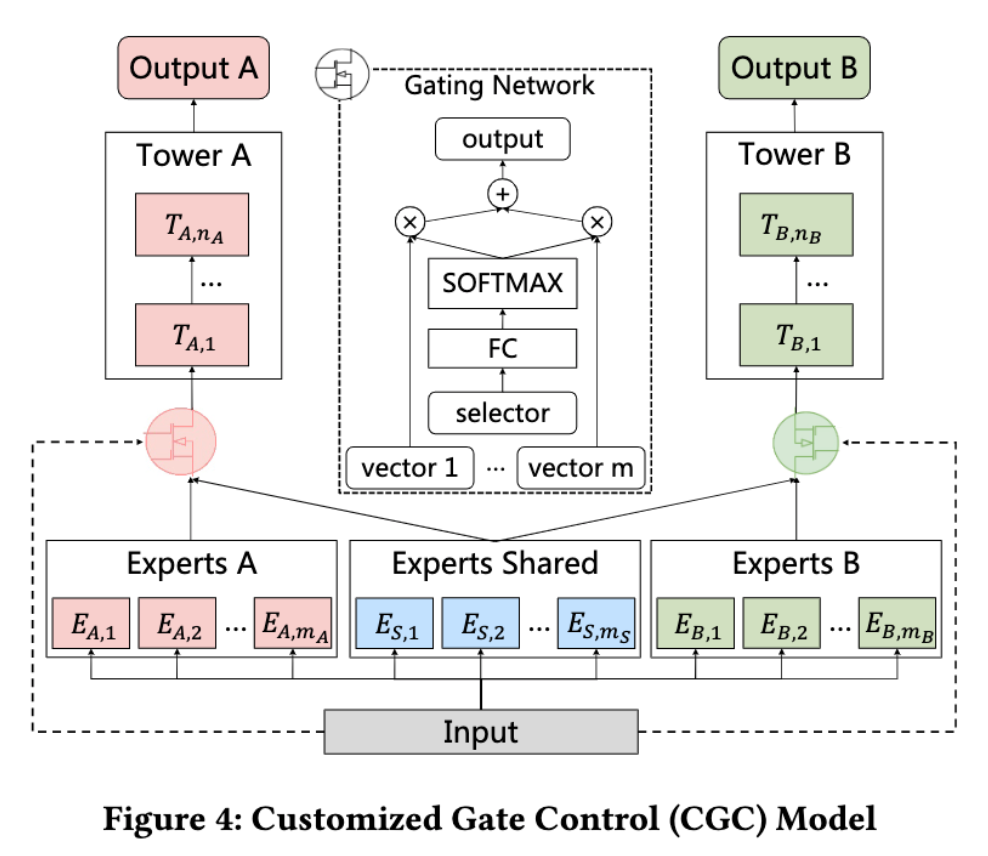
如上图所示，各模块结构的含义如下：

• shared experts：共享的专家网络组，即上图 Experts Shared 中的$E_{S,1}$等；
• task-specific expert：各个任务专享的专家网络组，例如 Experts A；
• task-specific tower：各个任务的输出塔，例如 Tower A；
• task-specific Gating：各个任务的门控网络，例如 Tower A的入口与Experts的连接处；

从上述结构可以看得出来，shared experts 会与所有任务链接，学习共享信息，而 task-specific expert 只会受到自己任务的影响，task-specific tower 则是由 task-specificGating 将对应的 task-specific expert 和 shared experts 组合后作为其输入的。这一过程可以表述称如下数理公式：

\begin{array}{l} 
y^k(x)=t^k(g^k(x))
\\
g^k(x)=w^k(x)S^k(x)
\\
w^k(x)=Softmax(W^k_g x)
\\
S^k(x)=[E^T_{(k,1)},E^T_{(k,2)},\dots ,E^T_{(k,m_k)},E^T_{(s,1)},E^T_{(s,2)},\dots ,E^T_{(s,m_s)}]
\end{array} 

其中，公式(1)表示任务k的输出结果，公式(3)表示门控网络的结构，公式(2)则表示基于门控网络将公式(4)中的专家网络组融合的过程。可以发现其与MMOE最大的区别便是不同Task之间除了共享的 Shared Experts 网络组之外还有各自独享的 Task-specific Experts，这也是接下来的 PLE 模型的核心组成模块。

5 PLE

基于 CGC 的结构，PLE（Progressive Layered Extraction）则是一个升级版本的结构，它扩增了 Experts 之间的交互，结构如下所示：

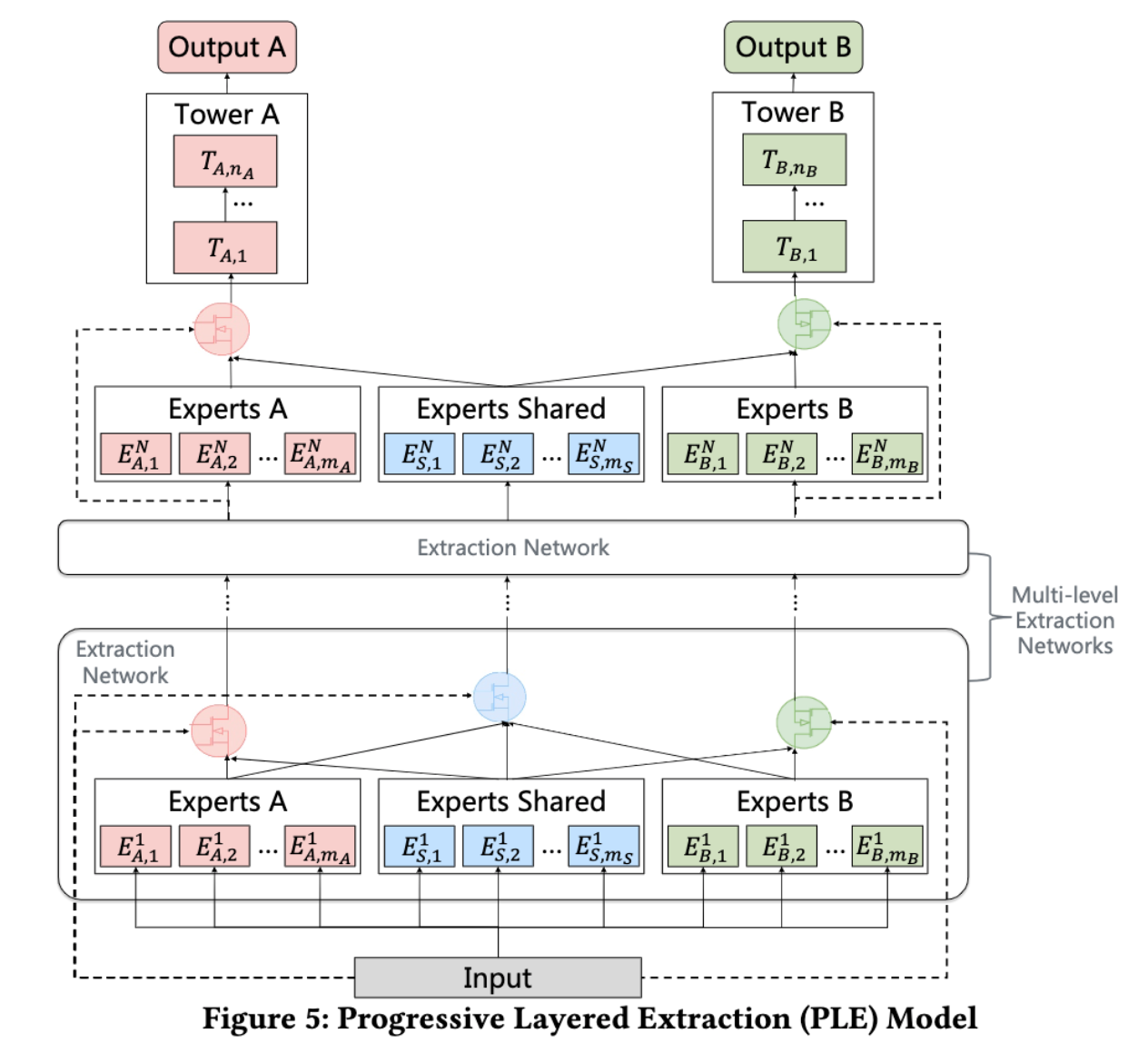
可以清晰的看到，其与CGC不同的是增加了多级的 Extraction Networks，而每一级的Extraction Networks 基本与CGC一致，旨在提取更高级别的共享信息。可以发现，每层 Shared Experts 吸收了下层的所有网络结构信息，而任务独享的 Task-specific Experts 则仅从其自己对应模块和Shared Experts中获取共享信息。整个过程可以简化成：

$$y^k(X)=t^k(g^{k,N}(x))$$

6 MTL 类型总结

6.1 Single-Level MTL

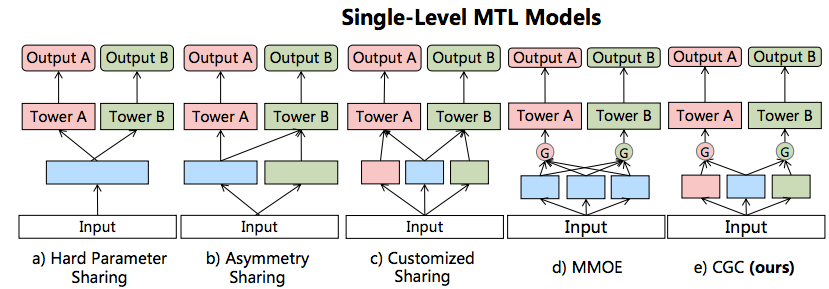
如上图所示，是5个经典的Single-Level MTL模型：

1. Hard Parameter Sharing：最常见的MTL模型，底层的模块是share的，然后共享层的输出分别进入到每个Task的Tower中。当两个Task相关性较高时，用这种结构效果一般不错，但任务相关性不高时，会存在负迁移现象，导致效果不理想。

2. Asymmetry Sharing（不对称共享）：不同Task的底层模块有各自对应的输出，但其中部分任务的输出会被其他Task所使用，而部分任务则使用自己独有的输出。交叉共享的部分需要认为定义，变数较多。

3. Customized Sharing（自定义共享）：不同Task的底层模块不仅有各自独立的输出，还有共享的输出。2和3这两种结构同样是论文提出的，但相对不重点。

4. MMOE：是大家比较熟悉的经典 MTL。底层包含多个 Expert，然后基于门控机制，不同任务会对不同 Expert 的输出进行过滤。

5. CGC：这就是本文重点介绍的一个，与 MMOE 的区别就是每个 Task 有自己独享的 Experts。

6.2 Multi-Level MTL

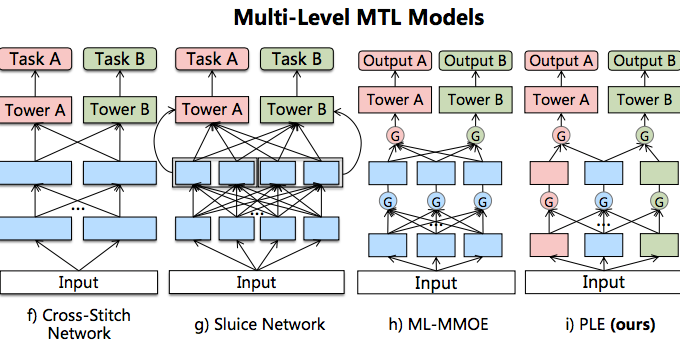
如上图所示，是4个经典的 Single-Level MTL 模型：

1. Cross-Stitch Network（”十字绣”网络）：出自论文《Cross-stitch Networks for Multi-task Learning》。

2. Sluice Network（水闸网络）：出自论文《Sluice networks: Learning what to share between loosely related tasks》.

3. ML-MMOE：前文已经有介绍。

4. PLE：这便是本文重点介绍的对象。

7 MTL 的 Loss 优化

在传统的MTL任务中，一般设定各个任务样本空间一致，然后训练的时候将各个任务的 loss 加权求和作为模型优化的总 loss 即可：

$$L(\theta_1, \dots , \theta_K, \theta_s)=\sum_{k=1}^K w_k L_k(\theta_k, \theta_s)$$

但实际上，不同Task的样本空间可能是不一致的。如下图所示。例如，假设 item 的 share 按钮在详情页，那么用户必须先 click 后，才能进行 share的动作，所以 share 的样本应该是 click 的一个子集，而不能粗暴的将没有 click（自然没有share）的样本也作为 share 的负样本，如此是有偏的。

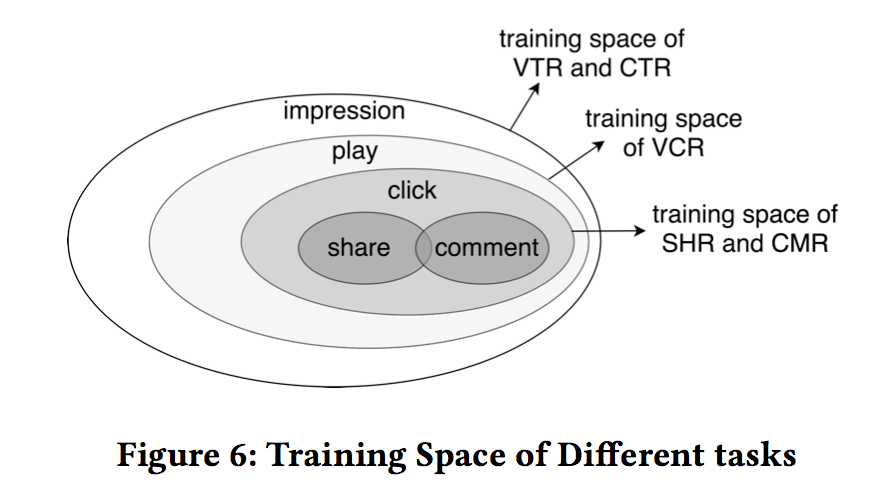
故，最终PLE在训练的时候 loss 构建如下：

$$L_k(\theta_k,\theta_s)=\frac{1}{\sum_i \delta_k^i} \sum_i \delta_k^i loss_k(\hat y_k^i (\theta_k, \theta_s),y_k^i)$$

其中，$\delta_k^i$是一个示性变量，表示第i个样本是否属于第k个 Task 的样本空间，实际上起到了样本 loss入场的筛选过滤作用。

除此之外，该团队还从 Multi-task learning 对 loss weight 敏感的角度出发，为了兼顾静态 weight 不如动态 weight 有效，并且不用像阿里提出的帕累托最优这种复杂的方式来优化。他们最终采用人共设置初始 loss weight，但是在不同的 train step 会进行 update，具体方式如下所示：

$$w_k^{(t)}=w_{k,0} \times \gamma_k^t$$

其中，$w_{k,0}$是人工设置的初始 loss wight，$\gamma_k$也是权重衰减的超参数，$t$则是 training step。

此优化确实较为合理，笔者在实际中也取得了效果。从数理角度理解，拆分样本空间后，预测的是每个阶段行为的条件概率，而不是联合改了，相对模式更容易学习。但是，此优化不仅限于PLE模型，实际上对任何一个MTL模型都适配的。

8 Code

由于本文重点讲解的是 PLE 模型，且 CGC 模型也是 PLE 的一个组成部分，所以 MMOE 和 CGC 的 code 在此就不提，咱们重点介绍一下 PLE 模型的结构模块代码。

from .multiTaskModel import multiTaskModel
from modules.experts import *
def gate(input, unit, name = "gate"):
    net = tf.layers.dense(inputs=input, units=unit, name='%s/dense' % name)
    gate = tf.nn.softmax(net, axis=1, name='%s/softmax' % name)
    return gate
    
def pleLayer(input_list, num_expert, num_task, dnn_dims, is_training, name = "pleLayer"):
    expert_feat_list = []
    # num_task + 1 experts
    for label_id in range(num_task + 1):
        for expert_id in range(num_expert):
            # buile expert
            expert_dnn = dnn(input_list[label_id], dnn_dims, is_training=is_training, usebn=True, activation="tf.nn.leaky_relu",
                             name='%s/label%d/dnn%d' % (name, label_id, expert_id))
            expert_feat_list.append(expert_dnn)

    experts_output_list = []
    for task_id in range(num_task):
        # build gate, unit equals task & share expert's nums
        gate_feat = gate(input = input_list[task_id], unit = num_expert * 2, name = '%s/gate%d' % (name,task_id))
        gate_feat = tf.expand_dims(gate_feat, -1)
        # staking，task & share experts
        experts_feat = tf.stack(expert_feat_list[task_id*num_expert:(task_id+1)*num_expert] +
                                expert_feat_list[-num_expert:], axis=1, name="%s/feat" % name)
        # attention
        task_input = tf.multiply(experts_feat, gate_feat, name = '%s/task%d/multiply' % (name,task_id))
        # reduce dim for tower input
        task_input = tf.reduce_sum(task_input, axis=1, name = '%s/task%d/output' % (name,task_id))
        experts_output_list.append(task_input)
    # share expert gate
    gate_feat = gate(input=input_list[num_task], unit=num_expert * (num_task+1), name='%s/gateshare' % (name))
    gate_feat = tf.expand_dims(gate_feat, -1)
    # staking， all experts
    experts_feat = tf.stack(expert_feat_list, axis=1, name="%s/featshare" % name)
    # attention
    task_input = tf.multiply(experts_feat, gate_feat, name='%s/taskshare/multiply' % (name))
    # reduce dim for tower input
    task_input = tf.reduce_sum(task_input, axis=1, name='%s/taskshare/output' % (name))
    experts_output_list.append(task_input)
    return experts_output_list    

class ple(multiTaskModel):
    def __init__(self, params):
        self.expertNum = 4
        self.expertDims = [512,512,512]
        self.extractLevel = 3
        super(ple, self).__init__(params)

    def build_graph(self, features, is_training, params):
        dnn_feats = params['feature_columns']['dnn_feats']
        input = tf.feature_column.input_layer(features, dnn_feats)

        # task_input_list[-1] is share experts input
        task_input_list = [input for _ in range(self.lable_size + 1)]
        for level in range(self.extractLevel):
            task_input_list = pleLayer(task_input_list, self.expertNum, self.lable_size, dnn_dims = self.expertDims,
                                       is_training=is_training, name = "pleLayer%d" % level)

        tower_outputs = {}
        for i in range(self.lable_size):
            tower_dnn = dnn(task_input_list[i], self.dnnDims, name="tower_%d" % i, is_training=is_training)
            tower_output = tf.layers.dense(inputs=tower_dnn, units=1, name='tower_output_%d' % i,
                                           activation=tf.nn.sigmoid)
            tower_outputs['tower_output_%d' % i] = tower_output
        self.ctr_pred = tf.reshape(tower_outputs["tower_output_0"], [-1], name="ctr")
        self.cvr_pred = tf.reshape(tower_outputs["tower_output_1"], [-1], name="cvr")

代码整体没有什么难度，基本上就按照模型结构图来实现即可。唯一需要注意便是关键聚合层的维度对齐，支持灵活控制模型各个 Experts 模块的结构调整即可。

参考文献
腾讯 at RecSys2020最佳长论文 - 多任务学习模型PLE
深度神经网络中的多任务学习汇总
【论文笔记日更10】腾讯PLE模型（RecSys 2020最佳论文）
多目标优化（三）recsys2020最佳长论文奖PLE
Google多任务模型
多目标学习在推荐系统的应用(MMOE/ESMM/PLE)
推荐系统中的多任务学习

---