MMOE 模型解析

1 引言

本文介绍的MMOE模型全称是Multi-gate Mixture-of-Experts，来自 Google 在 2018 年 KDD 上发表的论文Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts。核心目标是改善多任务学习在任务之间不太相关的时候效果不好的问题。下面有两个相关学习资源：

• 视频简介的youtube地址;
• 一个用keras框架实现的开源地址。

2 动机

多任务学习一般是为了在训练多个相关任务的时候可以使得它们之间能够共享信息，提高学习效率和模型的泛化能力。但实际应用中往往难以如此理想化，因为任务之间往往相关性不够强，这时候就容易产生以下两个问题：

负迁移（negative transfer）：即网络表现变差
跷跷板现象（seesaw phenomenon）：也就是个别任务相对于独立训练获得提升，但其他任务效果下降。

论文团队在实际中也做了这方面的实验，它们仿真了不同相关性的数据集，然后在他们上面测试模型的训练效果，如下图所示：

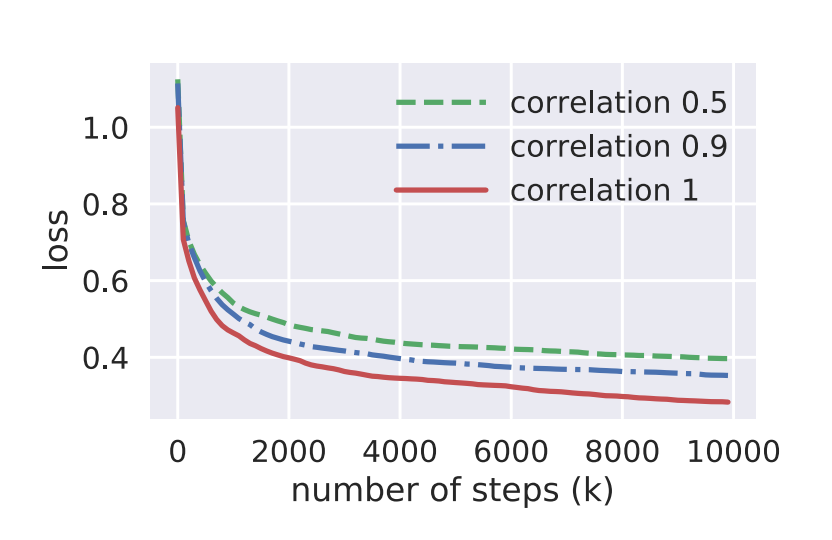
上图中的 correlation 是 Pearson相关性系数，从中可以看出相关性越高 loss 收敛的速度越快，值越小，说明效果越好。

在实际中，大多数任务也不足够相关，例如笔者自身的经验，在某电商瀑布流推荐场景，其中点击与查看价格相关性尚可（约0.48），但是收藏乃至成交等越深的行为与其相关性就越差了（<0.1）。有时候也不能够直接判断任务之间的相关性，但无论如何，解决相关性不高的多任务学习本身就是一个很有实际意义的工作。

3 模MMOE型

在MMOE模型提出来之前，也有一些相关的探索，论文作者也提到他们与MMOE之间的关系。

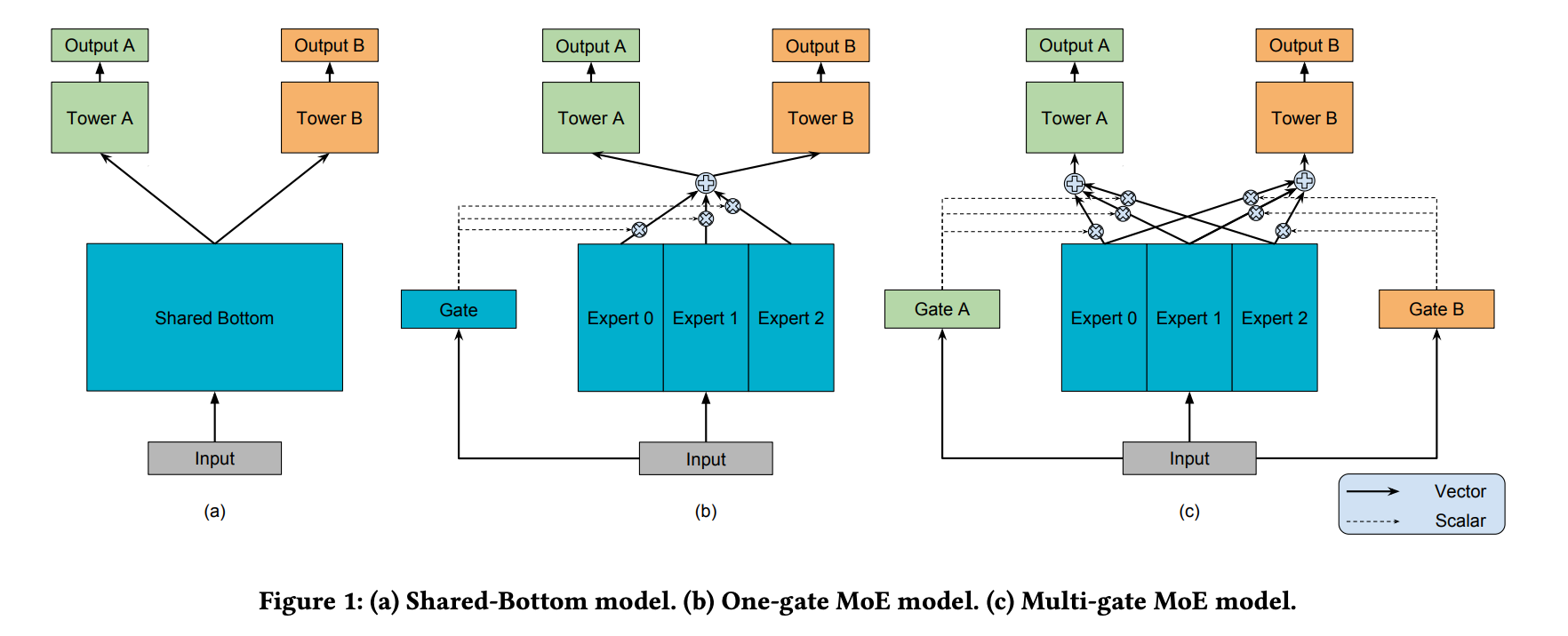
入上图所示，(a) 和 (b)是两个较为基础的shared embedding模型。

图 (a) 表示的是Shared-Bottom model，input 层之后进入模型 shared 的 bottom 模块，一般也就是一个 DNN 结构。之后，分别进入每个任务自己的 Tower，例如图中的 Tower A 和 Tower B，得到最终每个 Task 的 output。整个过程可以简单的用下述公式来表述：

$$y^k = h^k (f(x))$$

其中，

• k 表示第几个目标 Task;
• h 表示每个 Task 各自的 Tower 网络;
• f 则表示地步共享的 bootom 网络。

图 (b) 表示的是MOE模型，其与（a）比较显著的区别有2处：

• input 层后共享的 bootom 结构改成了多个 Experts 网络，图中是3个，并且各自参数不共享；
• input 层出了进入共享的 Experts 网络外，还用来生成 Task 各自的 Gate 网络，作为 Experts 进入每个 Task Tower 网络的门控权重。

可以发现，MOE 通过 input 生成 Gate 是为了赋予每个 Experts 网络进入 Task Tower 的权重，也是一种 Attention 的思想。其模型结构也以简单的总结如下公式：

$$y^k = h^k(\sum_{i=1}^n g_i f_i(x))$$ $$g = Softmax(W_{g}x)$$

其中，g 便是 Gate网络，i 表示第 i 个 Experts 网络。可以发现在 Gate 网络对 Experts 的输出进行加权求和之后，直接进入每个 Task 的 Tower 网络，所以每个 Tower 的 input 是一样的。

图 (b) 表示的是MMOE模型，也是论文作者提出的结构。其与 MOE 最大的区别就是：

对于每个 Task 都有用自己独享的 Gate 网络结构。

如此，每个 Task 可以根据任务需要，利用自己的 Gate 网络计算每个 Experts 进入 Tower 的权重，Gate 部分可简述为下列公式：

$$Gate^k = Softmax(W_{gk}x)$$

在实际中，作者实验也证明相关性较高的任务 MMOE 其实效果不明显，与 MOE 相差无异。但是在相关性较差的数据上，效果就与MOE拉开一定的差异，如下图所示。

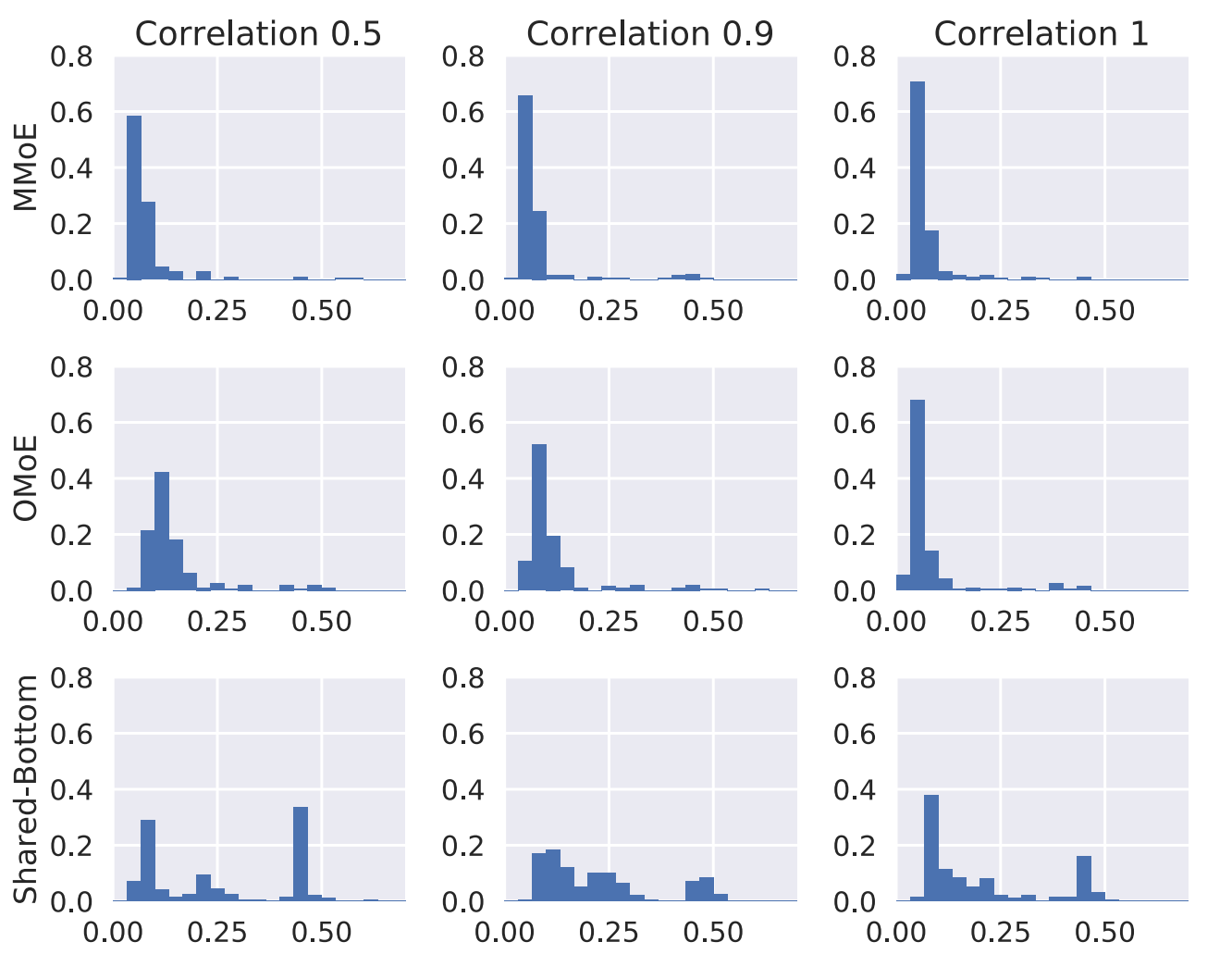
不过这也和数据集和操作过程有一定关系，笔者在实际工作中发现两个相关问题：

• 在大数据集且控制其他变量条件下，MMOE 往往很难与一般的 Shared-bootom 网络结构显著的拉开差距；
• 在多场景建模中往往会有一定的的价值拟合不同空间的样本和目标；
• 还有一种假提升情况，也就是模型收敛速度较快，但是最终水位相差无几。
  （举例，例如在实际新模型回刷数据中，将 base model 和 MMOE 都从某一天开始刷数据，会发现在 AUC 或者 loss 等指标上，MMOE 很快并且连续一段时间始终好于 base model，然而随着数据的积累，这种 diff 逐渐较小直至最终极其微小，这一般就是新模型收敛速度快的原因，会给算法工程师一个很大幅度的假提升现象。）

4 Code

MMOE 这里有两个 coding 的矩阵提速的点：

• 在构建Shared-Experts网络结构的时候，Expert 网络的个数可以作为一个维度，即直接生成一个三维tensor：$input_dim \times expert_unit \times experts_num$
• Gate 网络也可以将 Task 的个数作为其一个维度来一次性生成一个三维 tensor:$input_dim \times experts_num \times tasks_num$

以上技巧在前文提到的keras框架实现的开源地址中有所体现。这里展示一个笔者自己按照图结构一个一个模块写出来的版本：

import tensorflow as tf
from .multiTaskModel import multiTaskModel

def gate(input, unit, name = "gate"):
    net = tf.layers.dense(inputs=input, units=unit, name='%s/dense' % name)
    gate = tf.nn.softmax(net, axis=1, name='%s/softmax' % name)
    return gate

class experts:
    def __init__(self, num_expert, num_task, dnn_dims, name = "experts"):
        self.num_expert = num_expert
        self.num_task = num_task
        self.dnn_dims = dnn_dims
        self.name = name

    def __call__(self, input, is_training):
        expert_feat_list = []
        for expert_id in range(self.num_expert):
            # buile expert
            expert_dnn = dnn(input, self.dnn_dims, is_training=is_training, usebn=True, activation="tf.nn.leaky_relu",
                             name='%s/dnn%d' % (self.name, expert_id))
            expert_feat_list.append(expert_dnn)
        # staking，Bxnum_expertxdim not Bx(num_expertxdim)
        experts_feat = tf.stack(expert_feat_list, axis=1, name="%s/feat" % self.name)

        experts_output_list = []
        for task_id in range(self.num_task):
            # build gate
            gate_feat = gate(input=input, unit=self.num_expert, name='%s/gate%d' % (self.name, task_id))
            gate_feat = tf.expand_dims(gate_feat, -1)
            # attention
            task_input = tf.multiply(experts_feat, gate_feat, name='%s/task%d/multiply' % (self.name, task_id))
            # reduce dim for tower input
            task_input = tf.reduce_sum(task_input, axis=1, name='%s/task%d/output' % (self.name, task_id))
            experts_output_list.append(task_input)
        return experts_output_list

class mmoe(multiTaskModel):
    def __init__(self, params):
        self.expertNum = 3
        self.expertDims = [512,256,128]
        super(mmoe, self).__init__(params)

    def build_graph(self, features, mode, params):
        is_training = (mode == tf.estimator.ModeKeys.TRAIN)
        user_feats = params['feature_columns']['user_feats']
        item_feats = params['feature_columns']['item_feats']
        partitioner = partitioned_variables.min_max_variable_partitioner(max_partitions=self.ps_num,
                                                                         min_slice_size=8 * 1024 * 1024)
        with tf.variable_scope("embedding_scope", values=features.values(), partitioner=partitioner) as scope:
            user_inputs = tf.feature_column.input_layer(features, user_feats)
            item_inputs = tf.feature_column.input_layer(features, item_feats)
            tf.logging.info("=" * 8 + "user_inputs shape is %s" % str(user_inputs.shape) + "=" * 8)
            tf.logging.info("=" * 8 + "item_inputs shape is %s" % str(item_inputs.shape) + "=" * 8)

            if self.task_type != ["predict"] and mode == tf.estimator.ModeKeys.PREDICT:
                batchSize = tf.reshape(features["batchSize"], [])
                user_inputs = tf.tile(user_inputs, [batchSize, 1])
            embed_inputs = tf.concat([user_inputs, item_inputs], axis=1)
            tf.logging.info("=" * 8 + "embed_inputs shape is %s" % str(embed_inputs.shape) + "=" * 8)

        nn_partitioner = partitioned_variables.min_max_variable_partitioner(max_partitions=self.ps_num,
                                                                            min_slice_size=1 * 64 * 1024)
        with tf.variable_scope("nn_scope", partitioner=nn_partitioner) as nn_scope:
            expertsNet = experts(self.expertNum, self.lable_size, dnn_dims = self.expertDims)
            task_input_list = expertsNet(embed_inputs, is_training=is_training)
            tower_outputs = {}

            for i in range(self.lable_size):
                tower_dnn = dnn(task_input_list[i], self.dnnDims, name="tower_%d" % i, is_training=is_training)
                tower_output = tf.layers.dense(inputs=tower_dnn, units=1, name='tower_output_%d' % i,
                                               activation=tf.nn.sigmoid)
                tower_outputs['tower_output_%d' % i] = tower_output
            self.ctr_pred = tf.reshape(tower_outputs["tower_output_0"], [-1], name = "ctr")
            self.cvr_pred = tf.reshape(tower_outputs["tower_output_1"], [-1], name = "cvr")

参考文献
多任务学习之MMOE模型
多任务学习模型详解：Multi-gate Mixture-of-Experts（MMoE ，Google，KDD2018）

---