深度学习的常用损失函数

1 引言

在深度学习中，损失函数（Loss Function）至关重要，它决定着深度模型的训练学习的方式，其设计的恰当与否，往往会影响到最终模型的有效性。
虽然在很多通用型任务上，业内逐渐形成使用惯例，（如点击率建模，默认都用对数损失，logloss），但对损失函数的认识越清楚，会有助于算法工程师在面临新任务时，在模型设计上事半功倍。

2 常用损失函数

损失函数的任务是：针对一个样本，度量模型的预估值 logit 即$\hat y$和对应真实 Label 即$y$之间的差异。

不同的损失函数有不同的含义，主要是模型学习逼近样本分布的方式。所以它是一个非负实值函数，主要特点为：恒非负；误差越小，函数值越小；收敛快。

基于距离度量的损失函数

• 均方差损失函数（MSE）；
• L2 损失函数；
• L1 损失函数；
• Smooth L1损失函数；
• huber 损失函数；

基于概率分布度量的损失函数

• Logloss；
• KL 散度函数（相对熵）；
• Cross Entropy 损失；
• Softmax 损失函数；
• Focal loss。

2.1 均方差损失函数（MSE）

$$MSE = \frac{1}{n} \sum_{i=1}^n (y_i - p_i)^2$$

其中，n 是样本量，$y_i$是第 i 样本的真实 label，$p_i$是模型的预测结果。

该损失函数一般是用在回归问题中，用于度量样本点到回归曲线的距离。它对离群点比较敏感，所以它不适合离群点较多的数据集。

import numpy as np
def MSE_Loss(y_true:list,y_pred:list):
    """
    y_pred:list，代表模型预测的一组数据
    y_true:list，代表真实样本对应的一组数据
    """
    assert len(y_pred)==len(y_true)
    y_pred=np.array(y_pred)
    y_true=np.array(y_true)
    loss=np.sum(np.square(y_pred - y_true)) / len(y_pred)
    return loss

2.2 L2 损失函数

$$L2 = \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - p_i)^2}$$

其中，n 是样本量，$y_i$是第 i 样本的真实 label，$p_i$是模型的预测结果。

L2 函数，即最小平方误差（(Least Square Error(LSE))，也叫作欧氏距离。其在独立、同分布的高斯噪声情况下，它能提供最大似然估计，所以常用在回归、模式识别、图像任务中。

import numpy as np
def L2_Loss(y_true:list,y_pred:list):
    """
    y_pred:list，代表模型预测的一组数据
    y_true:list，代表真实样本对应的一组数据
    """
    assert len(y_pred)==len(y_true)
    y_pred=np.array(y_pred)
    y_true=np.array(y_true)
    loss=np.sqrt(np.sum(np.square(y_pred - y_true)) / len(y_pred))
    return loss

2.3 L1 损失函数

$$L1 = \sum_{i=1}^n |y_i - p_i|$$

其中，n 是样本量，$y_i$是第 i 样本的真实 label，$p_i$是模型的预测结果。

L1 Loss 即最小绝对误差(Least Abosulote Error(LAE))，又称为曼哈顿距离，表示残差的绝对值之和。

但它有2个缺点：

• 残差为零处却不可导；
• 梯度始终相同。

更适用于有较多离群点的数据集，但由于上述的缺点使得不利于模型的收敛。为了缓解此问题，实际中如果使用的话，往往使用后文介绍的优化版 Smooth L1 Loss。

这里顺便提一个与其非常接近的 MAE，即平均绝对误差：

$$MAE = \frac{1}{n} \sum_{i=1}^n |y_i - p_i|$$

import numpy as np
def L1Loss(y_true:list,y_pred:list):
    """
    y_pred:list，代表模型预测的一组数据
    y_true:list，代表真实样本对应的一组数据
    """
    assert len(y_pred)==len(y_true)
    y_pred=np.array(y_pred)
    y_true=np.array(y_true)
    loss=np.sum(np.abs(y_pred - y_true)) / len(y_pred)
    return loss

2.4 Smooth L1损失函数

$$Smooth L1 = \begin{cases} \frac{1}{2}(Y-f(x))^2 & \quad\text{|Y-f(x)|<1} \\ |Y-f(x)|-\frac{1}{2} & \quad\text{|Y-f(x)|>=1} & \end{cases}$$

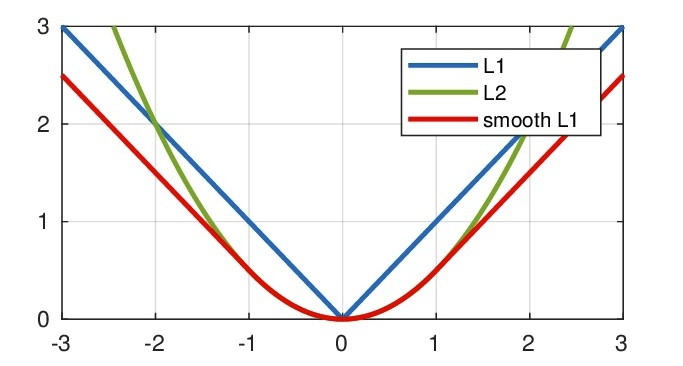
该函数是由 Girshick R 在 Fast R-CNN 中提出的，主要用在目标检测中防止梯度爆炸。其实际上是一个分段函数：

• 在[-1,1]，等价L2损失，解决了L1的不光滑问题；
• 在[-1,1]区间外，是L1损失，解决了L2离群点梯度易爆炸的问题。

def Smooth_L1_Loss(y_true_pred,y_true):
    assert len(y_true_pred)==len(y_true)
    loss=0
    for i_y_true_pred,i_y_true in zip(y_true_pred,y_true):
        tmp = abs(i_y_true-i_y_true_pred)
        if tmp<1:
            loss+=0.5*(tmp**2)
        else:
            loss+=tmp-0.5
     return loss

2.5 huber 损失函数

$$\left.\left.\left. Huber=\left\{ \begin{array} {ll}\frac{1}{2}(Y-f(x))^2 & |\mathrm{Y-f(x)}|<=\delta \\ \delta|Y-f(x)|-\frac{1}{2}\delta^2 & |\mathrm{Y-f(x)}|>\delta \end{array}\right.\right.\right.\right.$$

Huber 损失是 MSE 和 MAE 的结合，又称作 Smooth Mean Absolute Error Loss。

它克服了L1和L2的缺点：

• 不仅使损失函数具有连续的导数；
• 而且利用MSE梯度随误差减小的特性，可取得更精确的最小值。

但是，它有自己的缺点，不仅引入了额外的参数，而且选择合适的参数比较困难。

def huber_loss(y_pred,y_true,delta=1.0):
   assert len(y_pred)==len(y_true)
   loss=0
   for i_y_pred,i_y_true in zip(y_pred,y_true):
       tmp = abs(i_y_true-i_y_pred)
       if tmp<=delta:
           loss+=0.5*(tmp**2)
       else:
           loss+=tmp*delta-0.5*delta**2
   return loss

2.6 KL 散度函数（相对熵）

$$KL = \sum_{i=1}^n y_i \times log(\frac{y_i}{p_i})$$

其中，n 是样本量，$y_i$是第 i 样本的真实 label，$p_i$是模型的预测结果。

KL散度（ Kullback-Leibler divergence）也被称为相对熵，是一种非对称度量方法，即A、B两个分布，A对比B计算和B对A计算结果不一样。

相对熵是恒大于等于0的，当且仅当两分布相同时，相对熵等于0。KL散度可以用于比较文本标签或图像的相似性。

def kl_loss(y_true:list,y_pred:list):
    """
    y_true,y_pred，分别是两个概率分布
    比如：y_true=[0.1,0.2,0.8]
        y_pred=[0.3,0.3,0.4]
    """
    assert len(y_true)==len(y_pred)
    KL=0
    for y,fx in zip(y_true,y_pred):
        KL+=y*np.log(y/fx)
    return KL

2.7 Cross Entropy 损失

$$CE = -\frac{1}{n} \sum_{i=1}^n \sum_{j = 1}^m y_{ij} log(p_{ij})$$

其中，n 是样本数，m 是类别数，$y{ij}$是样本 i 所属类别 j 的示性变量，即属于时位1，否则为0，$p{ij}$表示预测的样本 i 属于类别 j 的概率。

交叉熵是信息论中的一个概念，最初用于估算平均编码长度，在深度学习中往往用于评估当前训练得到的概率分布与真实分布的差异情况。

为了使神经网络的每一层输出从线性组合转为非线性逼近，以提高模型的预测精度，一般配合softmax激活函数，在多分类问题中常常被使用。

def CrossEntropy_loss(y_true:list,y_pred:list):
    """
    y_true,y_pred，分别是两个概率分布list
    比如：y_true=[[0.1,0.9],[0.2,0.8],[0.4,0.6]]
         y_pred=[[0.3,0.7],[0.1,0.9],[0.4,0.6]]
    """
    assert len(y_true)==len(y_pred)
    cate_size = len(y_true[0])
    loss=0
    for y,fx in zip(y_true,y_pred):
        loss+=-sum([y[i] * np.log(fx[i]) for i in range(cate_size)]
    return loss

2.8 LogLoss 函数

$$LogLoss = -\frac{1}{n}\sum_{i=1}^n (y_i log(p_i) + (1 - y_i) log(1 - p_i))$$

其中，n 是样本量，$y_i$是第 i 样本的真实 label，$p_i$是模型的预测结果。

对数损失（logarithm loss）也被称为对数似然损失，实际上是交叉熵损失在二分类任务下的特例。其假设样本服从伯努利分布，利用极大似然估计的思想求得极值，它常作为二分类问题的损失函数，一般结合 sigmoid 输出函数使用。

def Log_loss(y_true:list,y_pred:list):
    """
    y_true,y_pred，分别是两个概率分布
    比如：y_true=[0.1,0.2,0.8]
         y_pred=[0.3,0.3,0.4]
    """
    assert len(y_true)==len(y_pred)
    loss=0
    for y,fx in zip(y_true,y_pred):
        loss+=-y * np.log(fx)
    return loss

2.9 Focal loss

$$FL = -\frac{1}{n}\sum_{i=1}^n (\alpha (1-p_i)^{\gamma} y_i log(p_i) + (1 - \alpha) p_i^{\gamma} (1 - y_i) log(1 - p_i))$$

其中，n 是样本量，$y_i$是第 i 样本的真实 label，$p_i$是模型的预测结果。

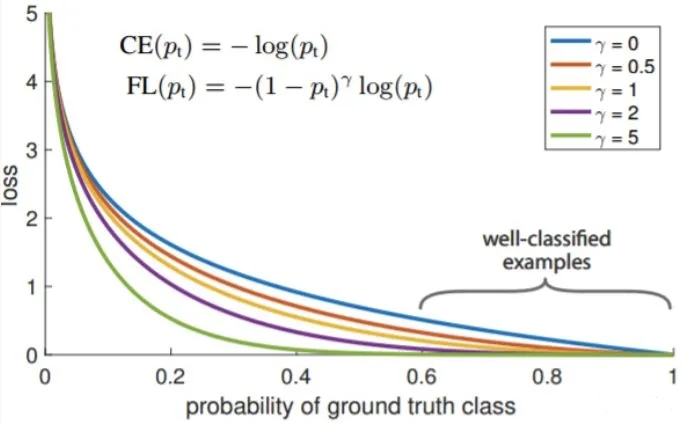
Focal Loss 的引入主要是为了解决难易样本不均衡的问题，注意有区别于正负样本不均衡的问题。易分样本虽然损失很低，但是数量太多，对模型的效果提升贡献很小，模型应该重点关注那些难分样本.
因此需要把置信度高的损失再降低一些性质：

• 当样本分类错误时，$p_t$趋于0，调变因子趋于1，使得损失函数几乎不受影响;
• 如果正确分类，$p_t$将趋于1，调变因子将趋向于0，使得损耗非常接近于0，从而降低了该特定示例的权重。

如下图，聚焦参数（γ）平滑地调整易于分类的样本向下加权的速率。

其中：

$$p_{\mathbf{t}}= \begin{cases} p & \mathrm{if~}y=1 \\ 1-p & \text{otherwise} & & \end{cases}$$

3 交叉熵的渊源

3.1 交叉熵与信息论

交叉熵（Cross Entropy）出自 Shannon 信息论，主要用于度量两个概率分布间的差异性信息。

假设 p 表示真实分布，q 表示预估分布，那么 $H(p,q)$ 就称为交叉熵：

$$H(p,q) = \sum_i p_i \cdot log \frac{1}{q_i} = -\sum_i p_ilog(q_i)$$

要追溯它的源头，需要再回到信息论中，信息量的表示方式：$I(x) = -log(p(x))$
$x$表示一个事件，$p(x)$表示事件 x 发生的概率，$I(x)$则表示信息量。
根据$log$函数的性质，事件发生概率越小时，它一旦发生后的信息量就越大。

假设随机变量 x，有两个独立的概率分布 $P(x)$ 和 $Q(x)$，怎么度量两个分布的差异呢？

使用 KL 散度（Kullback-Leibler (KL) divergence），又称相对熵。

KL散度的计算公式：

$$D_{KL}(q||p) = \sum_{i = 1}^n q(x_i) log \frac{q(x_i)}{p(x_i)}$$

其中，n为事件的所有可能性种类，D 的值越小，表示 Q 分布和 P 分布越接近。

我们简单做一下分解：

$$\begin{aligned} & \mathrm{} \\ D_{KL}(q||p) & =\sum_{i=1}^n q(x_{i})\log q(x_{i})-\sum_{i=1}^n q(x_{i})\log p(x_{i}) \\ & =-H(q(x))+H(q,p) \end{aligned}$$

到这里，你可能已经发现他们之间的关联了。

在深度学习中的分类任务，我们想要度量模型预估是否准确，就可以通过度量样本的真实分布（Label）与预估分布（Predict）之间的距离来判断。我们令：

• 真实分布（Label）：Q(x)
• 预估分布（Predict）：P(x)

真实分布往往就是训练样本，是给定不变的，所以在$D_{KL}(q||p)$中需要关注和优化的就只有分解后的第二项$H(q,p)$，即交叉熵。

如果我们令 n 表示样本数，m 表示分类数，$y{ij}$是样本 label，$p{ij}$表示预测的概率。批量的交叉熵便是：

$$CE = -\frac{1}{n} \sum_{i=1}^n \sum_{j = 1}^m y_{ij} log(p_{ij})$$

如果在二分类任务中，那么 $y_{ij}$ 就只有 0 和 1 两类，所以交叉熵可以简化为：

$$CE = -\frac{1}{n} \sum_{i=1}^n (y_i log(p_{i}) + (1 - y_i)log(1 - p_{i}))$$

相信你已经看出来了，这就是 LogLoss。

我们以 Logloss 为例，接着用极大值点的方式（导数为0）来求解极大似然估计：

$$\begin{aligned} & \mathrm{} \\ \sum_{i=1}^n (y_i \frac{1}{p_{i}} + (1 - y_i)\frac{1}{p_{i} - 1}) = 0 \\ \sum_{i=1}^n (p_i - y_i) = 0 \\ \bar p = \frac{1}{n} \sum_{i=1}^n y_i \end{aligned}$$

这就解释了实际应用中，对于二分类任务（比如ctr预估）模型的预估期望是等于 Label 的均值的，所以我们往往用 pcoc 来判断模型在局部样本上是高估还是低估。

3.2 交叉熵与极大似然

区别：

• 交叉熵是度量分布差距的大小，越大代表越不相近；
• 似然函数是度量分布一样的概率，越大代表越相近。

实际上，最小化交叉熵函数的本质就是对数似然函数的最大化。

最大似然估计中采样需满足假设：独立同分布实验。

我们假设独立采样 n 个样本，样本分布为 q，预估分布为 p，那么就有：

$$\begin{gathered} L=\frac{1}{n}\sum_{i=1}^{n}log\prod_{j=1}^{m}p_{ij}^{q_{ij}}=\frac{1}{n}\sum_{i=1}^{n}log(p_{1}^{q_{1}}.p_{2}^{q_{2}}...p_{m}^{q_{m}}) \\ =\frac{1}{n}\sum_{i=1}^n(q_1log(p_1)+q_2log(p_2)+...+q_m log(p_m)) \\ =\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^m q_ilog(p_i) \end{gathered}$$

可以发现，实际上就是交叉熵的绝对值。

3.3 交叉熵损失的优势

为什么不能使用均方差做为分类问题的损失函数？

均方差损失适合回归：与激活函数叠加是个凸函数，即可以得到最优解。

均方差损失不适合分类：

• 与激活函数（Sigmoid/Softmax）叠加不是凸函数，就很难得到最优解。
• 求导结果复杂，运算量比较大。

交叉熵适合分类：

• 可以保证区间内单调；
• 梯度计算简单，纯减法。

正如上面所述，交叉上损失在梯度计算上也有优势。我们以常用的二分类任务为例，单条样本交叉熵公式为：

$$C = -(y log(p) + (1 - y)log(1-p))$$

其中，y 是 label，p 是深度模型输出，如果结合输出层和激活函数，就有：

$$p = \sigma{(z)} , z = w x + b$$

我们就可以分别推导出参数$w,b$的梯度，如下所示，可以发现非常简洁，只与$p - y$有关，即预估误差越大，梯度更新越快。

$$\begin{gathered} \frac{\partial C}{\partial p} &=& -(y \frac{1}{p} + \frac{y - 1}{1 - p})\\ &=& -(y \frac{1}{p(1 - p)} - \frac{1}{1 - p})\\ \frac{\partial C}{\partial z} &=& \frac{\partial C}{\partial p} \frac{\partial p}{\partial z} \\ &=& -(y \frac{1}{p(1 - p)} - \frac{1}{1 - p}) \cdot \sigma'(z) \\ &=& -(y \frac{1}{p(1 - p)} - \frac{1}{1 - p}) \cdot \sigma(z)(1 - \sigma(z)) \\ &=& p - y \\ \frac{\partial C}{\partial w} &=& \frac{\partial C}{\partial z} \frac{\partial z}{\partial w} = (p - y)x \\ \frac{\partial C}{\partial b} &=& \frac{\partial C}{\partial z} \frac{\partial z}{\partial b} = (p - y) \end{gathered}$$

同样的，如果是多分类，使用 softmax 激活函数 + 交叉熵损失，也有类似的性质。虽然推导起来复杂一些，但结果也是只和$p - y$有关，这里不再赘述。

参考文章：
深度学习之损失函数
六个深度学习常用损失函数总览
深度学习——损失函数
监督学习中的损失函数及应用研究

---