MIND（多兴趣）召回模型

1 引言

在深度学习召回算法领域，比较经典的包括了以下2大类：

• 基于 item2vec 模型构建在线的i2i召回；
• 基于 user2item 泛双塔模型构建在线的u2i召回；

当然还有2阶以上的召回，i2u2i、u2u2i等，在这里不做重点介绍，最终目的都是为了召回 item。

对于第一种，相信大家比较熟知的有从 word2vec 衍生出的item2vec、阿里的deepwalk以及FM等，核心方式都是离线构建出 item 的 Embedding，在online侧基于用户的行为序列，取其中的 item 作为 trigger 来进行倒排/近邻召回。

对于第二种，一般比较常用的有微软的 DSSM、Airbnb 的向量召回的以及 YouTubeDNN 模型。他们的核心原理都是构建 user 和 item 的泛化双塔结构，使得 user 和 item 侧的独立生成各自的 Embedding，之后一般进行点积计算余弦相关性来构建 logloss 的优化目标。online 侧一般基于 user 画像特征，结合 user 侧模型结构实时 infer 出 userEmbedding，并从 item 集合中进行近邻召回 TopK。

本文重点介绍的就是2019年阿里团队在 CIKM 上发表的论文《Multi-Interest Network with Dynamic Routing for Recommendation at Tmal》中提出的 MIND（多兴趣）召回模型。

2 动机

在 u2i 召回领域，最重要便是建立合适的用户兴趣模型，以构建用户兴趣的有效表示。

如上图所示，便是经典的电商推荐场景，在召回阶段需要快速召回数千个与用户相关的候选物品。在文章的业务场景中，每日uv量大约在10亿级别，每个 user 会与上百量级的 item 进行互动，而整个物品池在千万甚至亿级别。所以作者发现用户的兴趣具有显著的多样性。

那么如何有效地表示这种多样的用户兴趣是最关键的问题，在此之前已有不少方案：

• 协同过滤(itemcf, usercf)召回，是通过历史交互过的物品或隐藏因子直接表示用户兴趣， 但会遇到稀疏或计算问题
• 基于深度学习的召回，将user表示成 dense embedding，例如 DSSM、YouTubeDNN。但是这种单一embedding表示有局限性，对用户兴趣多样性表示欠佳，而增加 embedding 维度又会带来计算成本，并且也无法解决信息混合的问题。
• 基于 Attention 机制的兴趣表示，例如经典的 DIN 模型。但是，此结构为了有效提取与 item 的信息，需要针对每一个候选 item 应用 attention 来计算 user 的 embedding，主要应用场景是精排模块。当然，self-attention 可以避开候选 item 侧，但是其也就退化成了上一种 u2i 模型。

为了更好的表示用户多样的兴趣，同时又尽量避开上述方法的弊端，作者提出了 MIND（多兴趣）网络模型。其核心思想便是：

基于胶囊网络的动态路由算法来将用户兴趣表示成多个向量

3 胶囊网络与动态路由

在介绍 MIND 之前，我们需要介绍一下胶囊网络和动态路由这两个知识点，主要是因为它们是MIND模型作者的借鉴来源，熟悉它们有助于对MIND的理解，当然我们只捡其中最核心相关部分来详解。

3.1 模型起源

胶囊网络模型是2017年大名鼎鼎的 Hinton 在文章《Dynamic Routing Between Capsule》中提出的。

实际上，胶囊网络是为了解决CNN在图像识别上的问题。彼时，CNN识别效果很显著，其具有下面两个特性：

• 平移不变性（translation invariance ）：即不管图片的内容如何进行平移，CNN还能输出与之前一样的结果。这个性质由全局共享权值和 Pooling 共同得到的；
• 平移等变性（translation equivariance）：即如果你对其输入施加的变换也会同样反应在输出上。这由局部连接和权值共享决定。

但是其依然具有与一些问题，那就是对同一个图像的旋转版本会识别错误，学术上称为不具有旋转不变性。所以为了缓解这一问题，常常会做数据增强以及pooling的操作去增加鲁棒程度：

• 数据增强：给图片经过旋转，裁剪，变换等操作，让CNN能学习同一张图片不同的这些形态；
• pooling：使得网络减少对特征出现的原始位置的依赖；

以上两种方式往往可以提高模型的泛化能力，但同时丢失了对位置信息的捕获能力。胶囊网络就是为了赋予模型理解图像中所发生变化的能力，从而可以更好地概括所感知的内容。

3.2 胶囊网络

接下来重点了解一下Capsule（胶囊网络）的结构，我们将其与传统的神经元结构做一个对比，如下图所示。

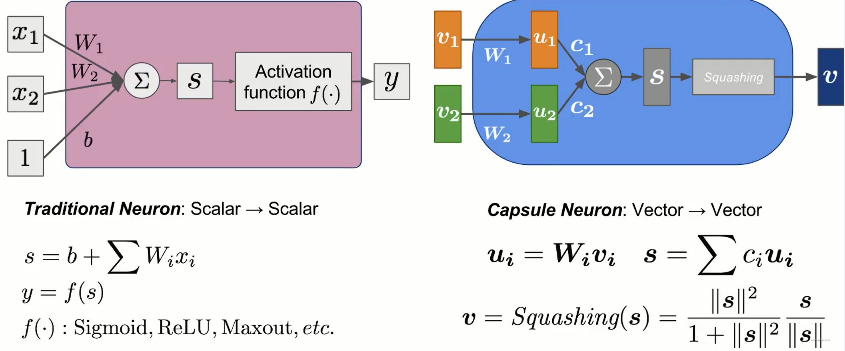
• 上图左侧是标准的神经元结构，其 input 与 output 都是标量，即 scalar to scalar 形式；
• 上图右侧便是一个胶囊结构，其 input 与 output 都是 vector，即 vector to vector 形式；

进一步解析 Capsule 结构，实际上这里的是不包含路由结构的单次胶囊结构。其输入是两个 vector，即 $v_1,v_2$，经过 $W_i$ 线性映射（矩阵乘）后得到新向量 $u_1,u_2$。之后，经过一组 $c_i$ 进行加权和得到汇总向量 $s$，$c_i$ 的计算方式后面会详细介绍。最后将 $s$ 经过Squashing算子便得到了输出向量 $v$。整体计算过程可以汇总如下公式组：

$$\begin{array}{l} u_i = W_i v_i \\ s = \sum c_i u_i \\ v = Squashing(s) = \frac{||s||^2}{1 + ||s||^2} \frac{s}{||s||} \end{array}$$

对于Squashing算子，我们可以发现:

• 其右边的项就是为了做 norm，来归一化量纲，同时保留了向量的方向。
• 而左侧项则是根据 $s$ 的模 $||s||$ 的大小来对结果进行压缩，越大，该项约趋于1，相反则趋于0。

如此便会有：

当$||s||$比较大的时候，一般是具有大值的长向量，则有$v \approx \frac{s}{||s||}$；
当$||s||$比较小的时候，一般是具有小值的短向量，则有$v \approx s||s||$；

为了进一步了解该函数的性质，我们基于标量构建Squashing算子的函数图如下。

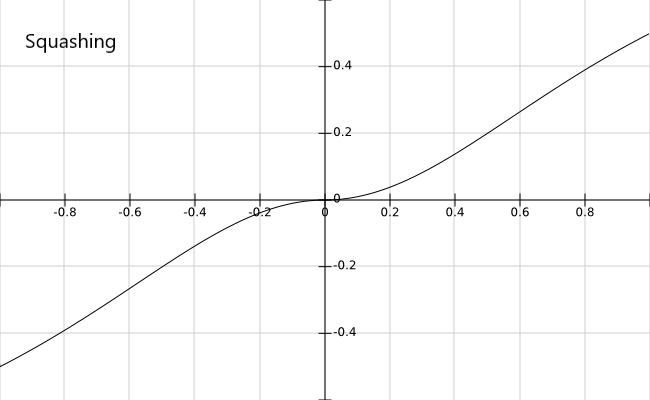
值得注意的是，实际上$W_i$是需要学习的变量，而$c_i$并不是，其为迭代计算的超参数，重点将在下一节介绍。

3.3 动态路由

基于前面的胶囊结构，动态路由实际上就是其中叠加一个迭代计算的过程，如下图所示的是原始论文对该算法的描述。

可以看到，先对每个胶囊初始化一个迭代参数$b_i$，并通过其生成权重$c_i$，在每一次迭代完成之后，更新迭代参数$b_i$。

这样看不够清晰，由于其基于CNN介绍的，包括了多个 Layer。所以我们基于前一节的单层 Capsule（胶囊网络）转化成如下的计算公式：

$$\begin{array}{l} b_1^0 = 0, b_2^0 = 0 \\ for \quad r = 1 \quad to \quad R \\ \quad c_1^r, c_2^r = softmax(b_1^r,b_2^r) \\ \quad s^r = c_1^r u_1 + c_2^r u_2 \\ \quad a^r = Squashing(s^r) \\ \quad b_i^r = b_i^{r-1} +a^r u_i \end{array}$$

我们来简要说明一下整个流程：

• 先对每个 capsule 初始化一个$b_i=0$；
• 开始R轮迭代，每轮迭代做以下步骤：

  1. 对所有的$b_i$取 softmax，如此使得权重$c_i$总和为1
  2. 基于$c_i$对所有$u_i$进行加权求和得到$s$
  3. 对$s$应用 Squashing 算子，得到结果向量$a$
  4. 按照公式更新所有$b_i$，并开始下一轮迭代

可以看到，实际上权重$c_i$与 attention 中的 weights 生成机制很像，只不过在这里经过$b_i$作为迭代的中间参数，$b_i$实际上称为 routing logit。其初始化为0，就使得$c_i$初始值都一样，对每一个 capsule 的关注度一致，没有偏差，在后面经过学习进行迭代。

我们将这一迭代过程可视化出来更助于理解。

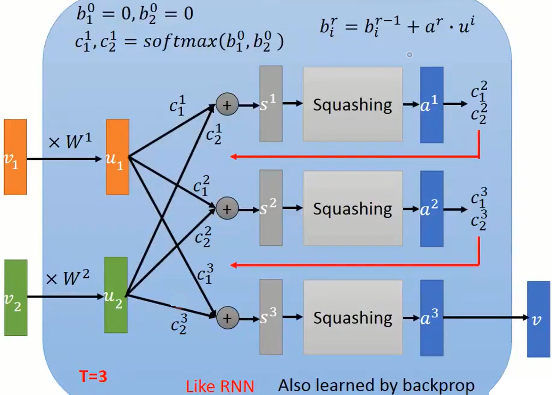
实际上，$v_i$可以称为 Capsule 网络的 input 向量，首先通过 $W_i$ 将其线性映射为 $u_i$，在这里 $v_i,u_i$ 的维度可能不同，前者是输入维度，后者是胶囊维度。并且，这一映射过程只在迭代前进行，迭代中只会用到映射后的 $u_i$。

在上图中，实际上有2个 capsule 向量，即 $u_1,u_2$，所以对应的会有 $b_1,b_2$ 两个初始参数以及其对应的迭代权重 $c_1,c_2$。他们的右上角标是指迭代的轮数 r。

例如，

1. r=0 的时候，$b_1^0=1,b_2^2=0$是初始化参数；
2. 然后经过 softmax 得到第1轮的 $c_1^1,c_2^1$ 权重；
3. 经过胶囊网络得到第1轮的结果向量 $a^1$；
4. 按照公式 $b_i^r = b_i^{r-1} + a^r u_i$ 便可迭代得到第2轮的 $b_1^1,b_2^1$ 参数;
5. 与是便得到更新后的第2轮的权重 $c_1^2,c_2^2$。

以此类推，直到最后一步迭代结束将 $a^3$ 最为最终结果向量输出。

既然 $b_i$ 不是学习得到的，而是迭代得到的，那么这里重点关注一下其更新公式。我们可以发现：

$b_i$ 在第r轮的变化项是 $a^r u_i$，如果该内积项值很大，则说明本轮的结果向量 $a^r$ 与此 capsule 向量 $u_i$ 很相似，那么参数 $b_i^r$ 便会增加，下一轮的权重 $c_i$ 同样变大，那么对应的 $a$ 中包含的 $u_i$ 的成分就会更大，二者向量就更近。实际上，这个 dynamic routing 的过程被看成是软聚类（soft-clustering）。

3.4 有效的原因

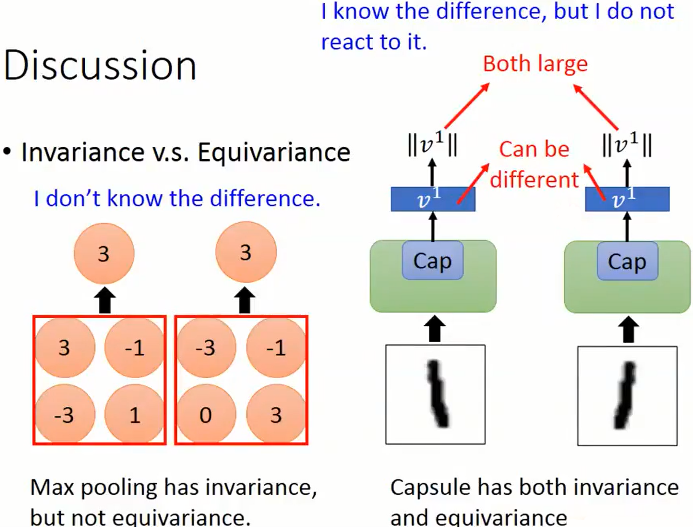
我们还以该技术的起源CNN图像识别为例，如下图所示，CNN实际上属于左侧结果，即对于图像的旋转是不变的，前面提过主要是通过一些手段加强训练的。而我们期望能够做到右侧的等变性，即能够感知到图像的变化，但又不影响结果。

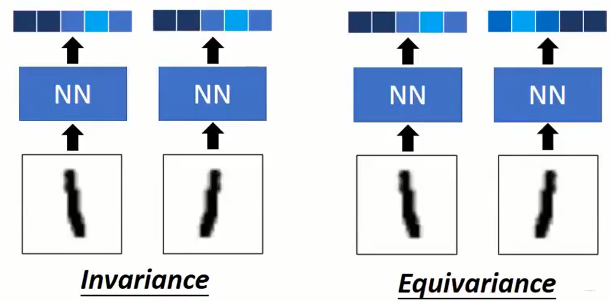
那为什么融入的 Capsule 网络结构就能够做到呢，我们举一个例子，如下图所示。

• 左侧是一个经典的 maxpooling 结构，其仅仅能做到 Invariance（不变性），即对于位置的变化无法感知，但能够做到结果一致。
• 右侧是一个 capsule 结构，首先其在结果上能够做到 Invariance（不变性），同时其过程中产生的 capsule 向量是不同的，即能够感知到图像旋转的变化，所以同时做到了 Equivariance（等变性）。

4 MIND模型

4.1 模型概述

经过前面的介绍，接下来理解 MIND 模型的结构就会简单的多。我们首先将其网络架构展示出来:

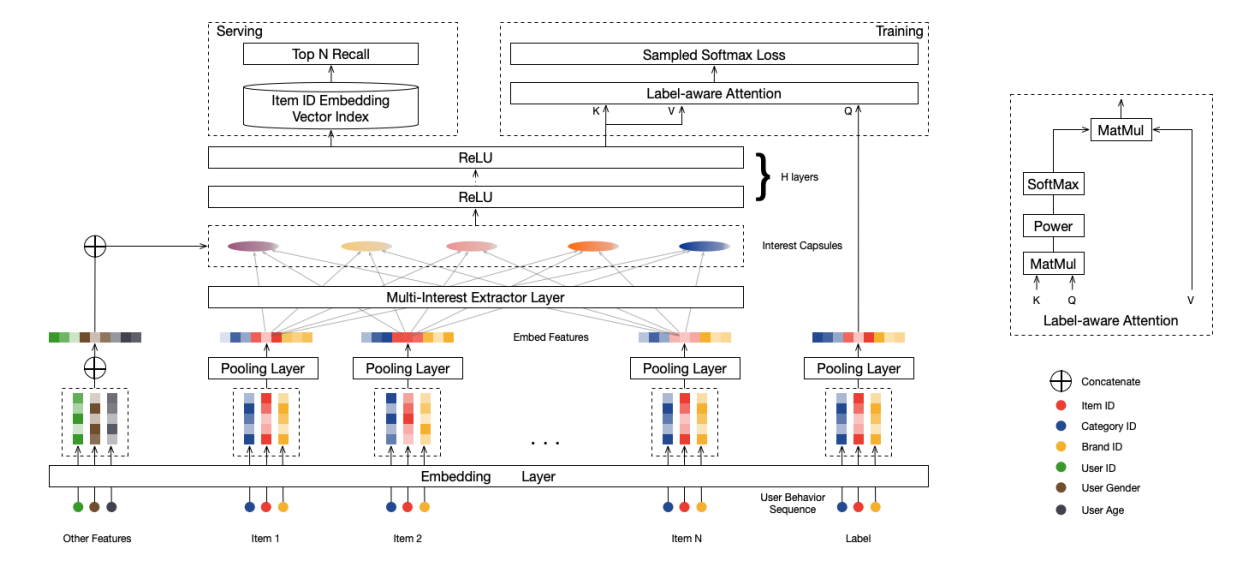
整个图大部分都是比较清晰的。

1. 底部是输入特征的 Embedding Layer，包括：
   • 用户属性特征（user ID，Age，Gender等，最左侧，concat 操作）
   • 行为序列特征（item ID，Brand ID，Category等，中间部分，pooling 操作）
   • 物品特征（item ID，Brand ID，Category等，最右侧，pooling 操作）
2. 用户行为序列特征会经过 Multi-Interest Extractor Layer（多兴趣提取层）抽取 Interest Capsules，即多个胶囊兴趣向量；
3. 将生成的 Interest Capsules 与用户属性特征 concat 到一起，经过两层 ReLU 激活函数的全连接网络；
4. 在 training 阶段，继续经过 Label-aware Attention（标签意识注意力）层，最终结合 Sampled Softmax Loss（负采样损失函数）即可完成训练；
5. 而在左上角表示的是 Serving 的时候，线上直接使用步骤3的结果（多兴趣向量）进行 TopK 的近邻召回即可。

需要注意的是，博主在工作中发现其中步骤3容易引起很多人误解：

也就是 Interest Capsules 抽取完之后的紧接着的两层全连接，这里很容易误解成将所有的兴趣向量与用户属性全部打平concat到到一起，然后经过两层FC，那结果不就是一个向量了吗？难道说这里还需要重新再把结果的长向量slice成多个Interest Capsules？答案显然NO！

仔细研究后文或者 code，便可以知道：这里的FC（全连接）是应用在 Interest Capsules 与用户属性特征 concat 后的最后一维上。

这里列举相关变量维度可能更容易理解：

• 假设 用户属性特征 concat 后维度是 (b, 1, n)，b 是 Batch Size，扩展出第二维的1是为了对齐
• 而提取的 Interest Capsules 层维度为 (b, k, m), k 是胶囊个数
• 全连接层 FC 的 Input 应该是上述二者的 concat 结果，即 (b, k, n+m)
• FC 层是应用在上述结果的最后一层进行线性映射，故其结果维度 (b, k, d)，d 是最终的 capsule 维度，其应该和 item 侧 的embedding pooling 结果一致，如此才能做 Attention。

接下来我们按照论文结构，介绍其中核心部分。

4.2 问题定义

这是一个召回问题，其任务目标毋庸置疑：

根据用户行为和属性等特征抽取多个用户兴趣的向量表示，然后利用其从 item 池子中进行TopK的近邻召回。

模型的输入在前一节已经介绍，主要是一个 user&item 的信息三元组 $(I_u,P_u,F_i)$，其中：

• $I_u$ 代表与用户u交互过的物品集，即用户的历史行为;
• $P_u$ 表示用户的属性，例如性别、年龄等；
• $F_i$ 表示为目标物品i的一些特征，例如 item id 和 category id 等。

基于上述，模型的核心任务：
将用户的属性$P_u$和行为特征$I_u$有效地映射成用户多兴趣 Embedding 向量集合，即

$$V_u = f_u(I_u, P_u) = (v_u^1, \dots , v_u^k) \in R^{d \times k}$$

其中，d 是用户最终的兴趣向量 Embedding 维度，k 表示兴趣向量的个数。

如此容易发现：

如果 $k=1$，即只有一个兴趣向量的话，模型本身就退化成传统的召回模型结构了，例如 YouTube DNN 这样。

而目标物品侧的映射方式:

$$\vec e_i = f_{item}(F_i)$$

其中 $\vec ei \in R^{d \times 1}$，于是其维度就和兴趣向量对其了，就支持后面的 Label-aware Attention 操作，而 $f{item}( \cdot )$ 是一个 Embedding & Pooling 层，即目标 item 的不同属性特征过 Embedding Layer 层后直接进行 sum/avg pooling。

最后也是将每个兴趣向量通过内积做相似度进行 TopK 的 item 召回：

$$f_{score} (V_i, \vec e_i) = \max_{1 \le k \le K} \vec e_i \vec V_u^k$$

4.3 Multi-Interest Extractor Layer（多兴趣提取层）

4.3.1 Dynamic Routing Revisit（动态路由）

在胶囊网络内，不管迭代多少次，实际上可以把整个网络看成2层，一个是 input 的低阶胶囊记为 $\vec ci^l \in R^{N_l \times 1}, i \in {1, \cdots , m}$，另一层便是 output 的高阶胶囊记为 $\vec c_j^h \in R^{N_h \times 1}, i \in {1, \cdots , n}$。其中 m, n 表示胶囊的个数，在 MIND 中m 那就是输入时序列的长度，n便是要抽取的兴趣向量个数，$N_l, N_h$ 表示两层胶囊的维度。 那么从低阶胶囊抽取高阶胶囊过程中的路由对数$b{ij}$一般如下计算：

$$b_{ij} = (\vec c_j^h)^T S_{ij} \vec c_I^l$$

其中，$S{ij} \in R^{N_j \times N_l}$ 是待学习的转换矩阵。接下来便可由 $b{ij}$ 计算出高低阶胶囊之间的加权权重 $w{ij}$（又称耦合系数），即直接对 $b{ij}$ 进行 softmax 计算即可：

$$w_{ij} = \frac{\exp{b_{ij}}}{\sum_{k = 1}^m \exp{b_{ik}}}$$

注意：这里计算的是某个低阶向量在不同胶囊之间的权重分配（总和为1），而不是某个胶囊里面不同低阶向量的权重分配

然后，便可以基于上述的权重来计算高阶胶囊j的中间过渡向量$\vec z_j^h$：

$$\vec z_j^h = \sum_{i=1}^m w_{ij} S_{ij} \vec c_i^l$$

最后，便是通过 Squashing 算子对中间变量进行压缩来得到结果的高阶胶囊向量 $\vec c_j^h$：

$$\vec c_j^h = Squashing(\vec z_j^h) = \frac{||\vec z_j^h||^2}{1 +||\vec z_j^h||^2 } \frac{\vec z_j^h}{||\vec z_j^h||}$$

上述是一次迭代的整个过程，看上去貌似与前述的胶囊网络不一样，实则不然。为了进一步促进理解，依然跟上一节一样，我们将单个高阶胶囊$\vec c_j^h$的2轮迭代的动态路由可视化出来，如下图所示。

将需要注意的是：原论文中的符号与前文和图示有些区别，且无高阶胶囊维度j：

• 论文的 $w{ij}$ -> 图示的胶囊加权权重$c{ir}$
• 论文的低阶和高阶胶囊 $\vec c_i^l, \vec c_j^h$ -> 图示的输入和输出向量 $v_i, v$
• 论文的聚合向量 $\vec z_j^h$ -> 图示的聚合向量$s$
• 论文的转化系数 $S{ij}$ -> 图示的转化矩阵 $W{i}$

4.3.2 B2I Dynamic Routing（B2I动态路由）

MIND 的作者实际上没有使用最原始的动态路由机制，而是使用了做了些许改造的B2I动态路由。它和原始的路由主要有3出处区别：(本部分以原文符号为主)

1. 共享映射矩阵。

   即所有的$S{ij}$（图中的$W{i}$）使用同一个S，主要原因是：

• input 胶囊（用户行为序列）的长度是不等的，统一映射矩阵利于减少参数提高泛化；
• 统一的映射矩阵可将商品映射的向量统一到同一空间；

1. 随机初始化陆游对数 $b_{ij}$

   由于共享了映射矩阵S，那么如果$b{ij}$初始化为 0，那么 softmax 后产生的所有的加权权重 $w{ij}$ 边都是相等的，之后各个兴趣胶囊在迭代中将会始终保持一致。作者实际上采用高斯分布来初始化 $b_{ij}$，这样使得每个胶囊（用户兴趣聚类中心）差异较大，从而度量多样的兴趣。实际上与K-means思想有点类似。

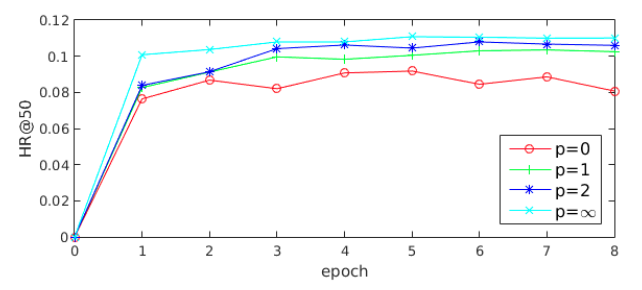
$b_{ij}$这一点可以从论文中的实验结果看到，使用方差更大的高斯函数来初始化routing logits效果更好:

但是，这里需要注意！！！
上面的设计并不一定是最优的，博主在实际应用中，发现参数不共享时，$b_{ij}$ 可以初始化为 0，效果反而更好，更有利于兴趣向量差异化，与业界其他业务交流也有类似的。

1. 动态的兴趣胶囊数量

   作者出发点是行为个数不一样的用户兴趣向量应该也有差异，行为越丰富兴趣像两个数相对给多一些，具体兴趣向量个数通过下面公式来确定。

$${K_u}' = max(1, min(K, log_{2}{(|L_u|)}))$$

4.4 Label-aware Attention Layer（标签意识注意力层）

实际上在多兴趣提取层和标签意识注意力层之间还夹杂着两个步骤：

1. 将用户的属性 Embedding 分别 concat 到每一个兴趣向量上；
2. 再经过两层激活函数为 ReLU 的全连接层来对其维度；

上述两部在前面部分已经介绍过，那么在此之后变得到了可以 feed 进入 Label-aware Attention Layer 的多兴趣向量。该层内的计算结构比较熟知，其实就是传统的 QKV 形式的 Attention 结构：

$$\vec v_u = Attention(\vec e_i, V_u, V_u) = V_u \quad softmax(pow(V_u^T \vec e_i, p))$$

其中，$\vec e_i$表示的目标商品向量，$V_u$就是用户的多兴趣向量组合，里面会有${K_u}’$个有效的兴趣向量。唯一的区别是，在做完内积操作后进行了一个幂次操作，$p$就是幂次的超参数。如此便会发现p是一个可调节的参数来调整注意力分布：

当 $p \longrightarrow 0$ 时，不同兴趣胶囊的注意力权重趋于相同；
当 $p >> 0$ 时，较大注意力权重的胶囊将会拉大这个优势，极端情况 $p \longrightarrow \infty$ 时，就变成了 hard-attention，即只有一个兴趣胶囊会生效；

值得注意的是，实际应用中（本人也有同样经验），p 小会使得胶囊之间差距缩小，反之可以使得兴趣胶囊差异性增加，实际线上效果也是 hard-attention 模式效果最优（如下图）

4.6 离线训练和线上服务

听过前面介绍的 Label-aware Attention Layer 生成用户u的聚合兴趣向量之 $\vec v_u$ 后，用户与物品i的交互的概率可以如下计算：

$$Pr(i|u) = Pr(\vec e_i | \vec v_u) = \frac{exp{(\vec v_u^T \vec e_i)}}{\sum_{j \in I} exp{(\vec v_u^T \vec e_j)}}$$

实际上就是一个对有所物品应用 softmax 算子

整体的目标函数是：

$$L = \sum_{(u,i) \in D} log{Pr(i|u)}$$

其中，D是训练数据包含用户物品交互的集合。

这里与 word2vec 类似，由于最后一层需要对所有物品应用 softmax 算子来计算概率。而有效物品的量一般很大，所以为了简化计算就转化成 SampledSoftmax 的方式，即只保留正样本，通过负采样生成负样本来做 binary task。

线上 serving 的时候，去除 label-aware 层，仅需要得到一个用户多兴趣向量表示的映射 $f_{user}$ 即可。通过 feed 用户画像信息，得到多个有效的兴趣表示向量，然后分别从物品集合中近邻检索 TopN 个物品即可（总共KN个物品）。

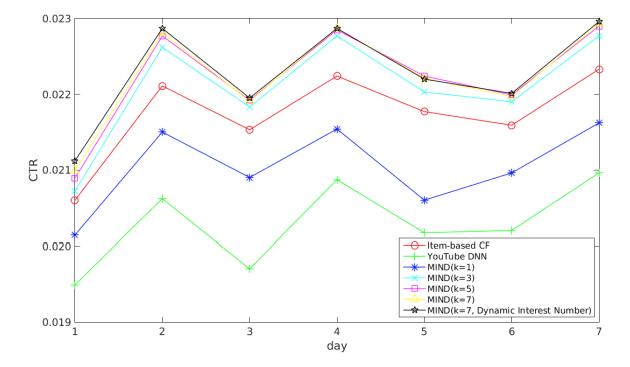
最后，作者实验了不同兴趣个数K的效果，发现最大兴趣个数K控制在5-7的时候表现较好。

5 code

这里给出一版自己实现的模型结构，篇幅原因，这里重点展示模型核心结构部分，其他模块省略，仅供参考。

from tensorflow.python.ops import partitioned_variables
from .recModelOpt import recModelOpt
import tensorflow as tf
from modules import dnn, capsuleLayer
import modules.featProcessor as fp

if tf.__version__ >= '2.0':
    tf = tf.compat.v1

class mindSampled(recModelOpt):
    
    def build_graph(self, features, mode, params):
            ......
            # build high_capsules
            seqFeats = tf.concat(seqFeatList, axis=2, name="seqFeats")
            seqFeats = tf.layers.dense(seqFeats, units=self.high_dim, activation=tf.nn.selu, name="seqFeatsDim")
            capsuleNet = capsuleLayer(capsule_config=capsule_config, is_training=is_training)
            high_capsules, num_capsules = capsuleNet(seqFeats, seqLen)

            # concatenate with user features
            userFeats = tf.tile(tf.expand_dims(user_inputs, axis=1),
                [1, tf.shape(high_capsules)[1], 1])
            interest_capsule = tf.concat([high_capsules, userFeats], axis=2, name="cap_concat")
            tf.logging.info("=" * 8 + "interest_capsule shape is %s" % str(interest_capsule.shape) + "=" * 8)

            interest_capsule = dnn(input=interest_capsule, dnnDims=self.userDnn, is_training = is_training,
                            usebn = False, l2_reg = self.l2_reg, name = "userDnn")
            # cap_norm = self.norm(interest_capsule, axis = 2, name = "user_norm")
            # item_norm = self.norm(self.item_vec, axis = 1, name = "item_norm")

            cap_att = tf.matmul(interest_capsule, tf.reshape(self.item_vec, [-1, self.high_dim, 1]))
            cap_att = tf.reshape(tf.pow(cap_att, self.sim_pow), [-1, self.num_interest])
            capsules_mask = tf.sequence_mask(num_capsules, self.num_interest)
            user_capsules = tf.multiply(interest_capsule, tf.to_float(capsules_mask[:, :, None]), name="user_capsules")
            padding = tf.ones_like(cap_att) * (-1e9)
            cap_att = tf.where(capsules_mask, cap_att, padding)
            cap_att = tf.nn.softmax(cap_att, axis=1)
            cap_att_stop = tf.stop_gradient(cap_att)
            if self.hardAtt:
                user_vec = tf.gather(tf.reshape(interest_capsule, [-1, self.high_dim]),
                                        tf.argmax(cap_att_stop, axis=1, output_type=tf.int32) + tf.range(
                                        tf.shape(cap_att_stop)[0]) * self.num_interest)
            else:
                user_vec = tf.matmul(tf.reshape(cap_att_stop, [tf.shape(cap_att_stop)[0], 1, self.num_interest]),
                                     interest_capsule)
            self.user_vec = tf.reshape(user_vec, [-1, self.high_dim], name="user_embed")
            self.user_emb = tf.reduce_join(
                tf.reduce_join(tf.as_string(user_capsules), axis=-1, separator=','),
                axis=-1, separator='|')
            self.item_emb = tf.reduce_join(tf.as_string(self.item_vec), axis=-1, separator=',')
            

class capsuleLayer:

    def __init__(self, capsule_config, is_training, name = "capsuleNet"):
        # max_seq_len: max behaviour sequence length(history length)
        self._max_seq_len = capsule_config.get("max_seq_len", 10)
        # max_k: max high capsule number
        self._num_interest = capsule_config.get("num_interest", 3)
        # high_dim: high capsule vector dimension
        self._high_dim = capsule_config.get("high_dim", 32)
        # number of Expectation-Maximization iterations
        self._num_iters = capsule_config.get("num_iters", 3)
        # routing_logits_scale
        self._routing_logits_scale = capsule_config.get("routing_logits_scale", 1.0)
        # routing_logits_stddev
        self._routing_logits_stddev = capsule_config.get("routing_logits_stddev", 1.0)
        self.bilinear_type = capsule_config.get("bilinear_type", 1)
        self._is_training = is_training
        self.name = name

    def squash(self, cap_interest):
        """Squash cap_interest over the last dimension."""
        cap_norm = tf.reduce_sum(tf.square(cap_interest), axis=-1, keep_dims=True)
        scalar_factor = cap_norm / (1 + cap_norm) / tf.sqrt(cap_norm + 1e-8)
        return scalar_factor * cap_interest

    def seq_feat_high_builder(self, seq_feat):
        with tf.variable_scope(self.name + '/bilinear'):
            if self.bilinear_type == 0:
                # 复用转换矩阵，后面路由对数可高斯初始化
                seq_high = tf.layers.dense(seq_feat, self._high_dim, activation=None, bias_initializer=None)
                seq_high = tf.tile(seq_high, [1, 1, self._num_interest])
            elif self.bilinear_type == 1:
                # seq_feat_high
                seq_high = tf.layers.dense(seq_feat, self._num_interest * self._high_dim, activation=None,
                                               bias_initializer=None)
            elif self.bilinear_type == 2:
                # seq_feat_high
                seq_feat =  tf.reshape(seq_feat, [-1, self._max_seq_len, self._high_dim])
                seq_high = tf.layers.dense(seq_feat, self._max_seq_len * self._num_interest * self._high_dim, activation=None,
                                               bias_initializer=None)
                seq_high = tf.reshape(seq_high, [-1, self._max_seq_len, self._num_interest, self._high_dim])
            else:
                # 扩增一维trans矩阵
                w = tf.get_variable(
                    self.name + '/transWeight', shape=[1, self._max_seq_len, self._num_interest * self._high_dim, self._high_dim],
                    initializer=tf.random_normal_initializer())
                # [N, T, 1, C]
                u = tf.expand_dims(seq_feat, axis=2)
                # [N, T, num_caps * dim_caps]
                seq_high = tf.reduce_sum(w[:, :self._max_seq_len, :, :] * u, axis=3)

        seq_high = tf.reshape(seq_high, [-1, self._max_seq_len, self._num_interest, self._high_dim])
        seq_high = tf.transpose(seq_high, [0, 2, 1, 3])
        seq_high = tf.reshape(seq_high, [-1, self._num_interest, self._max_seq_len, self._high_dim])
        return seq_high

    def routing_logits_builder(self, batch_size):
        if self.bilinear_type > 0:
            # 非共享转换矩阵，0初始化路由对数
            if self._is_training:
                # training的时候全部初始化
                routing_logits = tf.stop_gradient(tf.zeros([batch_size, self._num_interest, self._max_seq_len]))
            else:
                # 否则就是预估的时候同用户需要tile
                routing_logits = tf.zeros([self._num_interest, self._max_seq_len])
                routing_logits = tf.stop_gradient(tf.tile(routing_logits[None, :, :], [batch_size, 1, 1]))
        else:
            if self._is_training:
                routing_logits = tf.stop_gradient(tf.truncated_normal(
                    [batch_size, self._num_interest, self._max_seq_len],
                    stddev=self._routing_logits_stddev))
            else:
                routing_logits = tf.constant(
                    np.random.uniform(
                        high=self._routing_logits_stddev,
                        size=[self._num_interest, self._max_seq_len]),
                    dtype=tf.float32)
                routing_logits = tf.stop_gradient(tf.tile(routing_logits[None, :, :], [batch_size, 1, 1]))
        return routing_logits

    def __call__(self, seq_feat, seq_lens):
        # seq_feat padding
        cur_batch_max_seq_len = tf.shape(seq_feat)[1]
        seq_feat = tf.cond(
            tf.greater(self._max_seq_len, cur_batch_max_seq_len),
            lambda: tf.pad(tensor=seq_feat,
                paddings=[[0, 0], [0, self._max_seq_len - cur_batch_max_seq_len], [0, 0]],
                name='%s/CONSTANT' % self.name),
            lambda: tf.slice(seq_feat, [0, 0, 0], [-1, self._max_seq_len, -1]))

        seq_feat_high = self.seq_feat_high_builder(seq_feat)
        seq_feat_high_stop = tf.stop_gradient(seq_feat_high, name = "%s/seq_feat_high_stop" % self.name)

        batch_size = tf.shape(seq_lens)[0]
        routing_logits = self.routing_logits_builder(batch_size)

        num_capsules = tf.maximum(
            1, tf.minimum(self._num_interest, tf.to_int32(tf.log(tf.to_float(seq_lens)))))
        mask = tf.sequence_mask(seq_lens, self._max_seq_len)
        atten_mask = tf.tile(tf.expand_dims(mask, axis=1), [1, self._num_interest, 1])
        paddings = tf.zeros_like(atten_mask, dtype=tf.float32)

        for i in range(self._num_iters):
            capsule_softmax_weight = tf.nn.softmax(routing_logits, axis=1)
            capsule_softmax_weight = tf.where(tf.equal(atten_mask, 0), paddings, capsule_softmax_weight)
            capsule_softmax_weight = tf.expand_dims(capsule_softmax_weight, 2)

            if i + 1 < self._num_iters:
                # stop_gradient内迭代
                interest_capsule = tf.matmul(capsule_softmax_weight, seq_feat_high_stop)
                high_capsules = self.squash(interest_capsule)
                delta_routing = tf.matmul(seq_feat_high_stop, tf.transpose(high_capsules, [0, 1, 3, 2]))
                delta_routing = tf.reshape(delta_routing, [-1, self._num_interest, self._max_seq_len])
                routing_logits = routing_logits + delta_routing
            else:
                interest_capsule = tf.matmul(capsule_softmax_weight, seq_feat_high)
                high_capsules = self.squash(interest_capsule)
        high_capsules = tf.reshape(high_capsules, [-1, self._num_interest, self._high_dim])

        return high_capsules, num_capsules

参考文献
MIND召回介绍
浅谈胶囊网络与动态路由算法
AI上推荐 之 MIND(动态路由与胶囊网络的奇光异彩)
召回阶段的多兴趣模型——MIND
MIND模型(多兴趣)

---