PID 调控算法

1 引言

PID 全称 Proportional Integral Derivative，拆分项分别是 比例（Proportional）、积分（Integral）和微分（Derivative）。是应用最为广泛的控制模型，有 100 余年的历史了，应用场景有四轴飞行器，汽车的定速巡航等。
官方流程图：

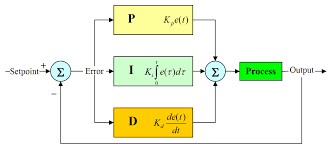
官方公式：

$$u(t)=K_pe(t)+K_i\int_0^te(\tau)d\tau+K_d\frac{d}{dt}e(t)=K_p[e(t)+\frac{1}{T_i}\int_0^te(\tau)d\tau+T_d\frac{d}{dt}e(t)]$$

其中：

• $K_p,K_i,K_d$ 分别是比例、积分、微分项的参数；
• $T_i,T_d$ 分别是积分、微分的时间常数；
• $e$ 为误差项=目标值(SP)-当前值(PV)；
• $t$ 为当前时间，$\tau$ 积分变数；

看上去很复杂，实际上比较简单，下面我们通过实例仿真的方式介绍下原理和效果。

2 算法详解

示例场景：我们以汽车的ACC巡航功能为例，假设起始速度为0，目标巡航车速为60。
最朴素的想法：以固定的加速度 a 加速到60后停止。
问题：实际上很难做到上述，因为控制器、传感器的输入、输出量是有延迟的，并且还有惯性的存在（比如，加速度并不能够直接从某个值骤降到0）。所以，比如当车速为58的时候，加速度不变，很容易超过60，超过后减速又很容易低于60，如此稳定性极差。

改进1: PID 中的 P-比例（Proportional）

既然有上述问题的存在，那么一个简单的缓解办法就是油门（加速度）不能一直不变，需要时刻监控车速，根据车速来调整，越接近目标值的时候，加速或者减速幅度越小，以便于车速稳定。

算法：当前时刻车速 $V_t$，目标车速 $V_a$，那么误差项 $e_t = V_a - V_t$，那么输出量为 $u_t = K_p * e_t$，即下一个单位时间提速 $u_t$。
通过代码模拟实际加速情况如下（$V_a = 60, K_p = 0.8$）：

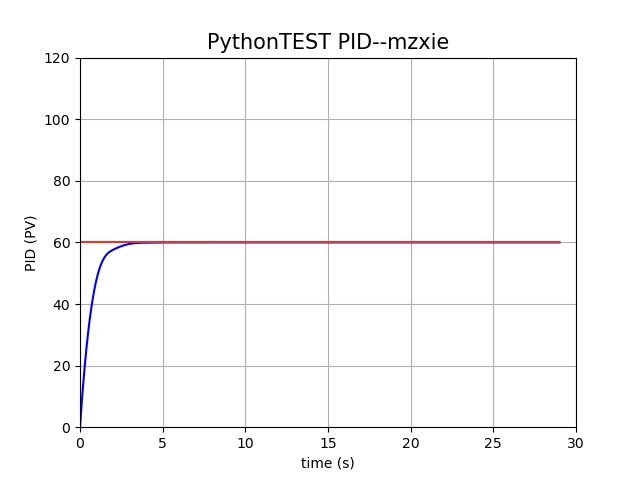
可以发现很快就趋近于目标值了。但实际上还是会存在问题：

实际中汽车会收到风阻、地面摩擦力等各种阻力，会使汽车自燃状态下速度逐渐减小，我们假设单位时间汽车车速收到的阻力综合效果会减速 $V_p$。

当我们把模拟代码加入此项后，情况如下（$V_P = 6$）：

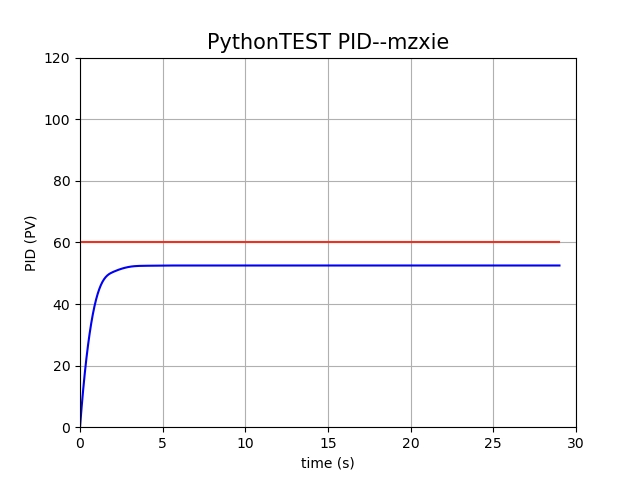
看上去最终车速停在了目标车速的下方，这个还是比较好证明的。因汽车最终的车速达到稳态后，则会有加速=阻力损失的状态，那么就有：

$$K_p (V_a - V_t) = V_p$$

代入参数可以解得最重的稳态速度

$$V_t = V_a - V_p/K_p = 52.5$$

问题：这一差距称为稳态误差，因此需要想办法来克服这一误差。

改进2: PID 中的 I-积分（Proportional）

积分项能够在比例单元的基础上，消除由比例调控造成的余差，能够对含有累计误差的系统进行误差修正，减小稳态误差。

我们来看实际情况中是怎么生效的，I项离散化后就是历史所有 $et$ 的累计和。$I_t = \sum{t=0}^T e_t$当我们把模拟代码加入此项后，情况如下（$K_i = 0.2$）：

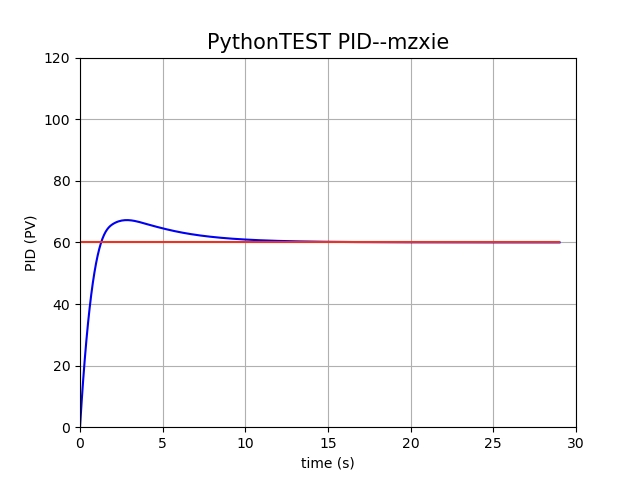
可以发现，最终速度可以很好的收敛到目标。

为什么能够做到这一点呢？相对也比较好证明，基于前面的稳态条件，此处需要达到稳态的话，需要满足：

$$K_i I_t + K_p \cdot e_t = V_p$$

一般 $K_i,K_p$ 都是正数，那么要想达到稳态，必须 $e_t = 0$，否则 $I_t$ 一直处于变化状态。而 $e_t = 0$ 则意味着 $V_t = V_a$，即在稳态达到的时候，车速最终也将在目标速度。

改进3: PID中的 D-微分（Derivative）

看似拥有P和I项之后，整个系统效果已经不错了，那么为什么还需要D项呢？

实际上，在现实工业系统中，大多数控制通道都是有一定延迟之后的。这时候就需要D这一微分项，它具有超前调节的作用，合适的值能够有效减少系统的超调量，减缓振荡以提高稳定性。

我们来对比一下，假设引入系统滞后性参数 $delay = 0.1$:

• 下左图为仅有P和I项，可见收敛前有一个比较大的峰值震荡；
• 相应的，在此基础上我们引入D项（$K_d=0.1$），结果如下右图，平缓了许多。

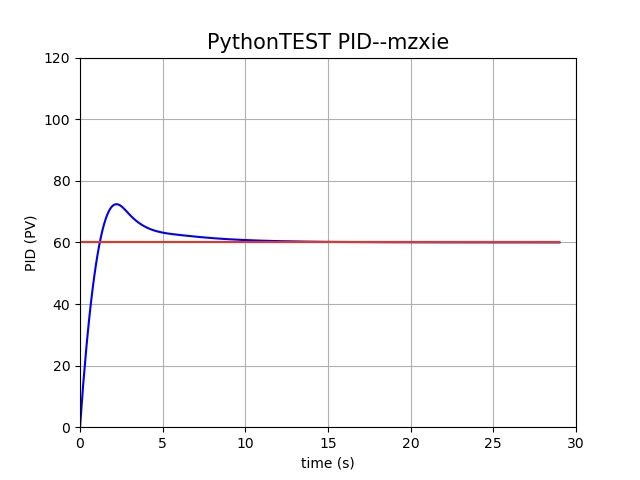
可以见到，PID中的三项分别是针对实际系统中的情况进行设计的，有时候D项对应的问题不明显的时候（例如系统延迟很低），确实P和I就够用了。

另一方面，就是各项超参数的设定，虽然也有一些参数调整的经验，但在实际应用中更多还是靠实际应用效果为准。

code

这里展示的是为了介绍构建的最简单的模型 code，实际工业应用远比此复杂，但底层逻辑相通，仅供参考。

import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import make_interp_spline

class PID:
    def __init__(self, P, I, D):
        self.Kp = P
        self.Ki = I
        self.Kd = D
        self.sample_time = 0.00
        self.current_time = 0
        self.last_time = self.current_time
        self.upper = 0
        self.lower = 0
        self.last_error = 0
        self.pre_error = 0
        self.inc = []
    def set_bound(self, upper, lower):
        self.upper = upper
        self.lower = lower

    def set_target(self, target):
        self.target = target

    def update(self, feedback_value):
        error = self.target - feedback_value
        delta_error = error - self.last_error
        # inc_error = error - 2 * self.last_error + self.pre_error
        self.inc.append(error)
        PTerm = self.Kp * error#比例
        ITerm = self.Ki * sum(self.inc) #积分
        DTerm = self.Kd * delta_error #微分
        self.output = PTerm + ITerm + DTerm
        # self.output = min(self.upper,max(self.output, self.lower))
        self.pre_error = self.last_error
        self.last_error = error


def test_pid(P, I , D, L, isdelay = True):
    pid = PID(P, I, D)
    T = 60.0
    pid.set_target(T)
    pid.set_bound(0.4,-0.4)

    END = L
    feedback = 0
    damper =  0.1 * T # 系统阻力
    feedback_list = []
    feedback_list.append(feedback)
    time_list = []
    time_list.append(0)
    setpoint_list = []
    setpoint_list.append(pid.target)
    output_last = 0

    for i in range(1, END):
        pid.update(feedback)
        output = pid.output
        delay = 0 if isdelay else output_last * 0.1
        feedback += output - damper + delay #PID控制系统的函数
        feedback_list.append(feedback)
        setpoint_list.append(pid.target)
        time_list.append(i)
        output_last = output

    time_sm = np.array(time_list)
    time_smooth = np.linspace(time_sm.min(), time_sm.max(), 300)
    feedback_smooth = make_interp_spline(time_list, feedback_list)(time_smooth)
    plt.figure(0)
    plt.grid(True)
    plt.plot(time_smooth, feedback_smooth,'b-')
    plt.plot(time_list, setpoint_list,'r')
    plt.xlim((0, L))
    plt.ylim((min(feedback_list)-0.5, max(feedback_list)+0.5))
    plt.xlabel('time (s)')
    plt.ylabel('PID (PV)')
    plt.title('PID simulation by python',fontsize=15)

    plt.ylim((0, 2*T))

    plt.grid(True)
    plt.show()

if __name__ == "__main__":
    # P
    test_pid(0.8, 0.0, 0.0, L=30)
    # P + I
    test_pid(0.8, 0.2, 0.0, L=30)
    # p + I + D
    test_pid(0.8, 0.2, 0.0, L=30, isdelay=False)
    test_pid(0.8, 0.2, 0.1, L=30, isdelay=False)

3 流量调控应用

场景：在互联网推荐中，经常需要针对一些物料定制分发量。比如新品保最低量，特殊品定量分发等。
差异：不同于ACC越早稳定到目标越好，需要的可能是尽量保留高效的pv，且逐步缓慢式的在规定时间结束前达到目标流量值。

参数设定：

• 某物料日内的流量目标值 $pv_a=2880$；
• 跳出条件点击目标 $clk_a=3$;
• 分片时间窗口 $P=1h$（平滑pv_a日内波动）；
• 调控时间窗口 $W=5m$（p是w的整数倍）；

那么W将是整个系统的更新频率，每个P内会更新12次；

假设当前时刻$t$，在某个分片$p$（8-9点）的某个调控窗口$w$（8:20-8:25）内。

算法步骤：

1. 统计实时流量：

   • 实时累计曝光$exp_t = 1000$，累计点击$clk_t=1$；
   • p和前一p的初始累计曝光$expp=970,exp{p-1}=840$;

2. 判断是否跳出，即$(clk_t>=clk_a)=False$;

3. 计算目标：

   • $t$所在窗口$p$内的总目标 $target_p=(2880/24)=120$；（简化为均分$pv_a/24$）
   • p开始到当前t的累积目标 $target_t = target_p \cdot (25/60) = 50$;
   • 假设上一p的累积目标 $starget{p-1} = 960$,那么当前 $starget_t = starget{p-1}+ target_t=1010$；

4. 计算误差：

   • $p$开始到当前$t$实际曝光 $pexp_t = exp_t - exp_p = 30$;
   • 当前$t$误差 $e_t = target_t - pexp_t = 20$;
   • 假设 $exp{t-1} = 980$,那么 $e{t-1} = target{t-1} - pexp{t-1} = 25$;
   • 积分误差 $ie_t = starget_t - exp_t = 10$;
   • 微分误差 $det = e_t - e{t-1} = -5$;

5. 计算调控输出：

   • $u_t = K_p \cdot e_t + K_i \cdot ie_t + K_d \cdot de_t$;
   • $u_t = max(min_u, min(u_t, max_u))$ 控制调控上下限；
   • 应用方式，可以基于$u_t$做插入分发量，或者转为权重进行调控。

当然实际中有很多可以优化点的，比如：

• 每个 $p$ 内的 $target_p$ 可以按照日内流量分布来加权计算更准确；
• $u_t$ 应用的时候可以考虑物料具体的效率。

整体来说，这是一个比较经典的PID算法应用示例，当然也可以看得出，我们还是需要从实际问题出发对算法做一定的调整以便于更好的服务于业务。

参考文献:
什么是PID？讲个故事，秒懂！
PID控制算法原理
PID算法的一般形式、原理、公式等

---