Transformer 解析

1 背景

算法工程师在成长道路上基本绕不开深度学习，而 Transformer 模型更是其中的经典，它在2017年的《Attention is All You Need》论文中被提出，直接掀起了 Attention 机制在深度模型中的广泛应用潮流。

在该模型中有许多奇妙的想法启发了诸多算法工程师的学习创造，为了让自己回顾复习更加方便，亦或让在学习的读者更轻松地理解，便写了这篇文章。形式上，在参考诸多优秀文章和博客后，这里还是采用结构与代码并行阐述的模式。

2 Transformer 概述

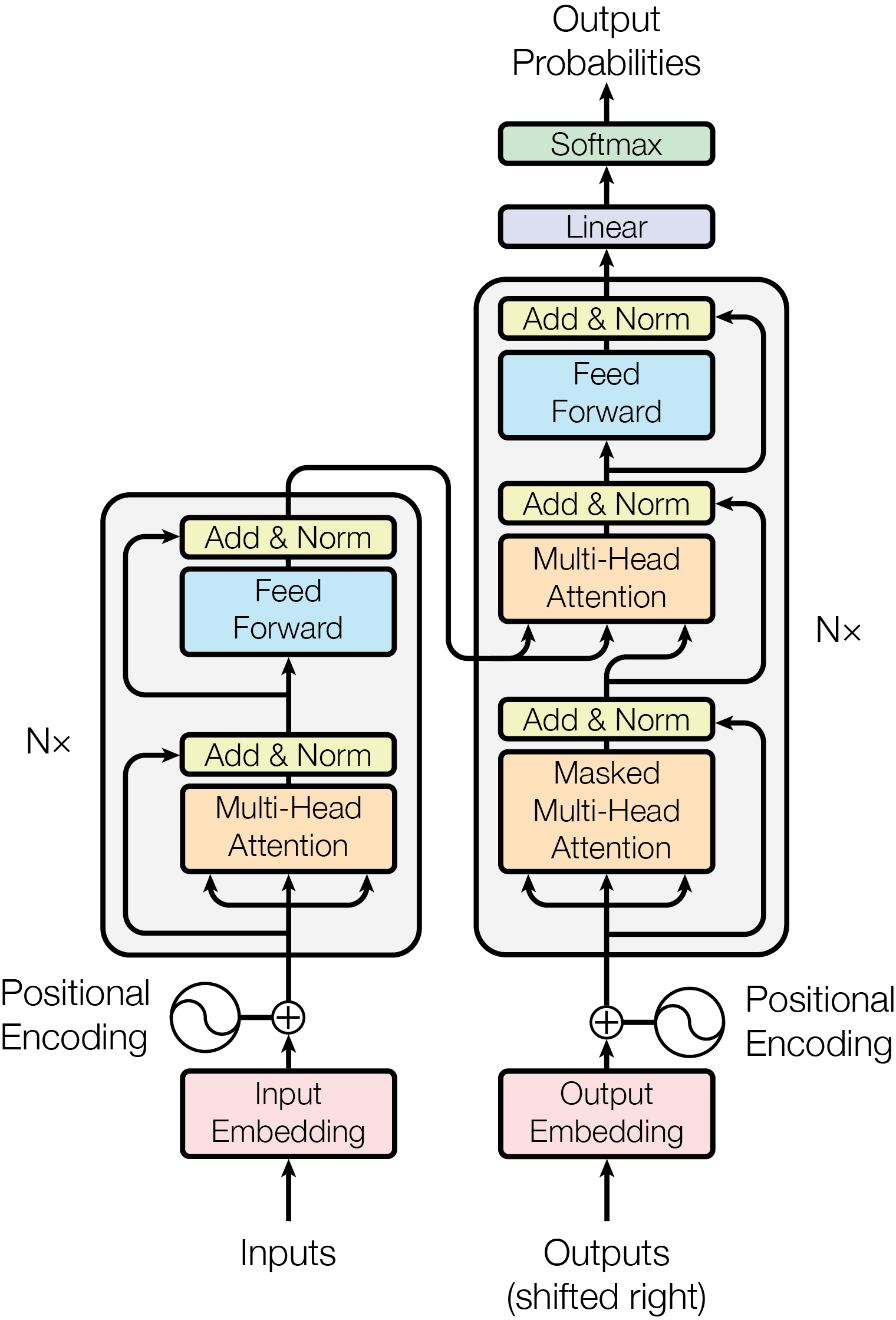
如上图所示的是论文中对 Transformer 模型的结构概述，自己初学时对此图有些难以理解。回过头来看，实际上作者默认读者是一个对深度学习较为熟悉的，所以隐去了部分细节信息，仅将最核心的建模思想绘制了出来。

在这里，我想再降低一下门槛，提高复习和阅读的舒适度。需要指出的是，论文提出该模型是基于nlp 中翻译任务的，所以是一个 seq2seq 的结构，如下图所示。

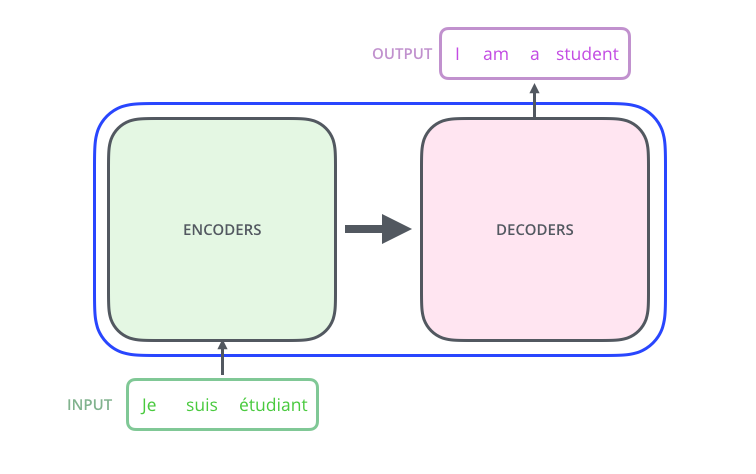
图中表明了输入的句子经过多个编码器 encoder 后再经过多个解码器 decoder 得到最后的预估结果。那么重点就在于以下四个部分：

• input
• encoder
• decoder
• output

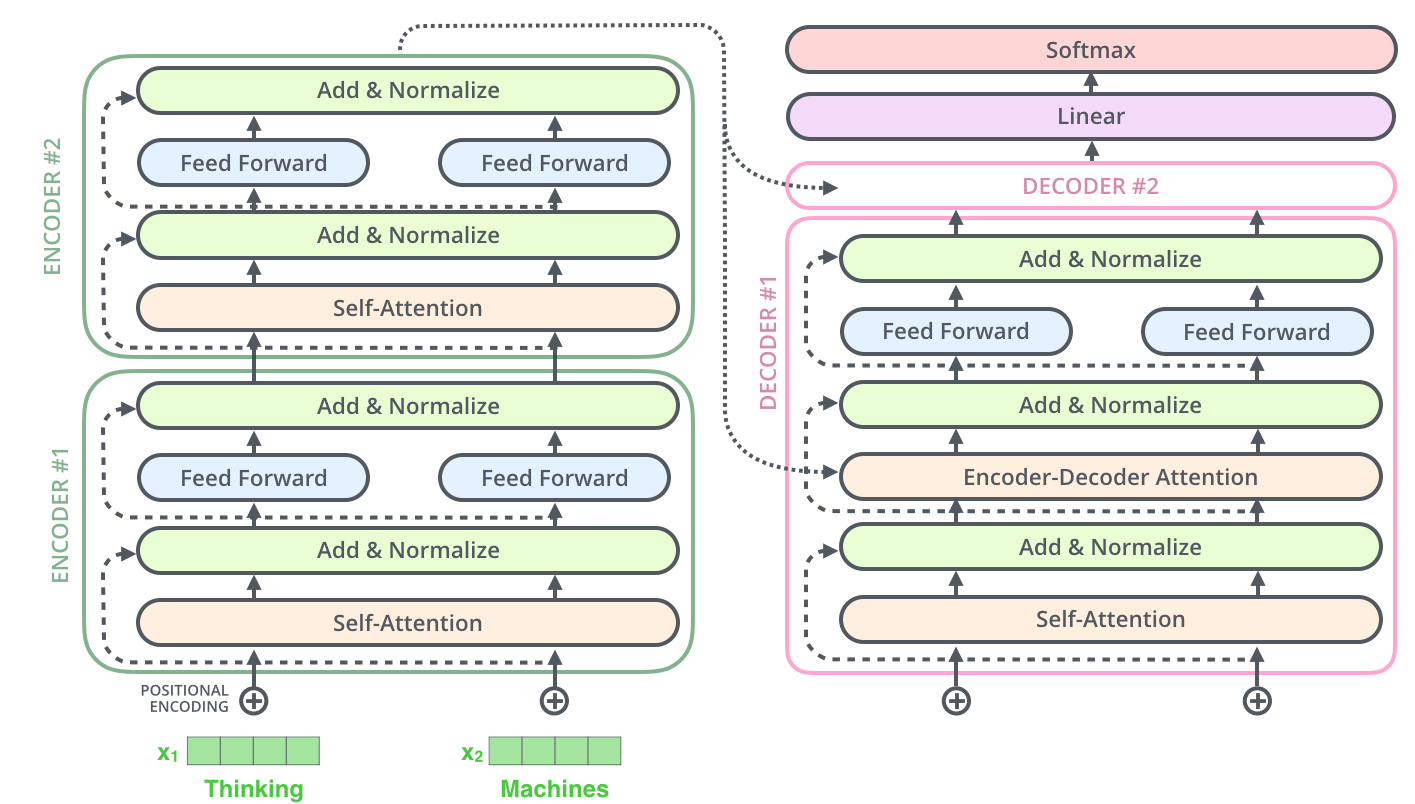
结合上述的模型图，将这四个部分详细展示的话可以表示成如下结构。实际上此图与论文中的结构图如出一辙，但是相对更易于理解一些。下面将基于此结构，结合 Kyubyong 的 tf 实现代码，详细分析每个模块。

3 模块解析

3.1 Input

模型核心的入口便是 train 方法模块，如下所示，在 input 有的情况下，前馈网络是比较清晰简洁的，只有 encode 和 decode，与模型结构图一致。其余的代码便是主要用来构建训练 loss 和优化器 opt 的。需要注意的是 encode 模块并不完全等价于模型结构图中的 encoder，后者是前者中的一部分。

def train(self, xs, ys):
   '''
   Returns
   loss: scalar.
   train_op: training operation
   global_step: scalar.
   summaries: training summary node
   '''
   # forward 前向
   memory, sents1, src_masks = self.encode(xs)    # 编码
   logits, preds, y, sents2 = self.decode(ys, memory, src_masks)    # 解码
 
   # train scheme
   y_ = label_smoothing(tf.one_hot(y, depth=self.hp.vocab_size))    # 平滑标签
   ce = tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits, labels=y_)    # softmax分类
   nonpadding = tf.to_float(tf.not_equal(y, self.token2idx["<pad>"]))  # 0: <pad>
   loss = tf.reduce_sum(ce * nonpadding) / (tf.reduce_sum(nonpadding) + 1e-7)

   global_step = tf.train.get_or_create_global_step()
   lr = noam_scheme(self.hp.lr, global_step, self.hp.warmup_steps)
   optimizer = tf.train.AdamOptimizer(lr)
   train_op = optimizer.minimize(loss, global_step=global_step)

   tf.summary.scalar('lr', lr)
   tf.summary.scalar("loss", loss)
   tf.summary.scalar("global_step", global_step)

   summaries = tf.summary.merge_all()

   return loss, train_op, global_step, summaries

进一步的，我们深入 encode 去看 input 在进入 encoder 前的一些预处理，如下代码所示。可以看到输入 xs 实际上包含三个部分：

• x: 被补全的句子映射的 tokenid 序列
• seqlens: 句子的长度
• sents: 原始句子

首先根据 tokenid 是否为0构建了 src_masks 源句掩码，接着将输入 x 进行词向量嵌入。

这里需要注意，code 中作者将词向量进行了缩放，系数是 $d_{model}^{0.5}$。而这一部分原始论文中是没有提及的。

之后，还进行了两步处理：

• 加上 positional_encoding：为了融入位置信息；
• 接一层 dropout：为了防止过拟合。

到此，输入的预处理便结束了，之后就如模型结构图所示，开始进入多个 encoder 进行编码了。

def encode(self, xs, training=True):
    '''
    Returns
    memory: encoder outputs. (N, T1, d_model)
    '''
    with tf.variable_scope("encoder", reuse=tf.AUTO_REUSE):
        x, seqlens, sents1 = xs    # 被补全的句子，句子长度，原句
 
        # src_masks 源句掩码
        src_masks = tf.math.equal(x, 0) # (N, T1) 掩码，标记补全位置
 
        # embedding 嵌入
        enc = tf.nn.embedding_lookup(self.embeddings, x) # (N, T1, d_model)    # 词嵌入 Input Embedding
        enc *= self.hp.d_model**0.5 # scale 对enc缩放，但是原论文中没有发现相关内容
 
        enc += positional_encoding(enc, self.hp.maxlen1)    # 位置嵌入
        enc = tf.layers.dropout(enc, self.hp.dropout_rate, training=training)     #Dropout 防止过拟合
        # 截止现在输入已被嵌入完毕
 
        ## Blocks Encoder 块
        for i in range(self.hp.num_blocks):    # 设定的Encoder块
            with tf.variable_scope("num_blocks_{}".format(i), reuse=tf.AUTO_REUSE):    #当前是第几个Encoder块
                # self-attention    多头注意力机制
                enc = multihead_attention(queries=enc,
                                          keys=enc,
                                          values=enc,
                                          key_masks=src_masks,
                                          num_heads=self.hp.num_heads,
                                          dropout_rate=self.hp.dropout_rate,
                                          training=training,
                                          causality=False)    # 多头注意力机制
                # feed forward    前向传播
                enc = ff(enc, num_units=[self.hp.d_ff, self.hp.d_model])
    memory = enc # 记住当前进度
    return memory, sents1, src_masks

3.2 Positional encoding

前面提到为了融入位置信息，引入了 positional_encoding 的模块。而位置编码的需求：

1. 需要体现同一个单词在不同位置的区别；
2. 需要体现一定的先后次序关系；
3. 并且在一定范围内的编码差异不应该依赖于文本长度，具有一定不变性。

官方的做法是：

$$PE_{(pos, 2i)} = sin(pos/10000^{2i/d_{model}})$$ $$PE_{(pos, 2i+1)} = cos(pos/10000^{2i/d_{model}})$$

其中：

• pos 是指词在句中的位置;
• i 是指位置嵌入 emb 的位置序号。

整个模块的代码如下所示。

def positional_encoding(inputs,
                        maxlen,
                        masking=True,
                        scope="positional_encoding"):
    '''Sinusoidal Positional_Encoding. See 3.5
    inputs: 3d tensor. (N, T, E)
    maxlen: scalar. Must be >= T
    masking: Boolean. If True, padding positions are set to zeros.
    scope: Optional scope for `variable_scope`.
    returns
    3d tensor that has the same shape as inputs.
    '''
 
    E = inputs.get_shape().as_list()[-1] # static 获取此向量维度 d_model
    N, T = tf.shape(inputs)[0], tf.shape(inputs)[1] # dynamic N为batch_size，T为最长句子长度
    with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
        # position indices    位置索引
        position_ind = tf.tile(tf.expand_dims(tf.range(T), 0), [N, 1]) # (N, T) 对张量进行扩展 1,T → N,T
 
        # First part of the PE function: sin and cos argument 位置嵌入方法
        position_enc = np.array([
            [pos / np.power(10000, (i-i%2)/E) for i in range(E)]
            for pos in range(maxlen)])
 
        # Second part, apply the cosine to even columns and sin to odds.  不同位置 使用sin和cos方法
        position_enc[:, 0::2] = np.sin(position_enc[:, 0::2])  # dim 2i
        position_enc[:, 1::2] = np.cos(position_enc[:, 1::2])  # dim 2i+1
        position_enc = tf.convert_to_tensor(position_enc, tf.float32) # (maxlen, E)
 
        # lookup
        outputs = tf.nn.embedding_lookup(position_enc, position_ind)
 
        # masks
        if masking:    # 是否需要掩码
            outputs = tf.where(tf.equal(inputs, 0), inputs, outputs) 
        # inputs中值为0的地方（为True的地方）保持值不变，其余元素替换为outputs结果。因为0的地方就是掩码的地方，不需要有所谓的位置嵌入。
 
        return tf.to_float(outputs)

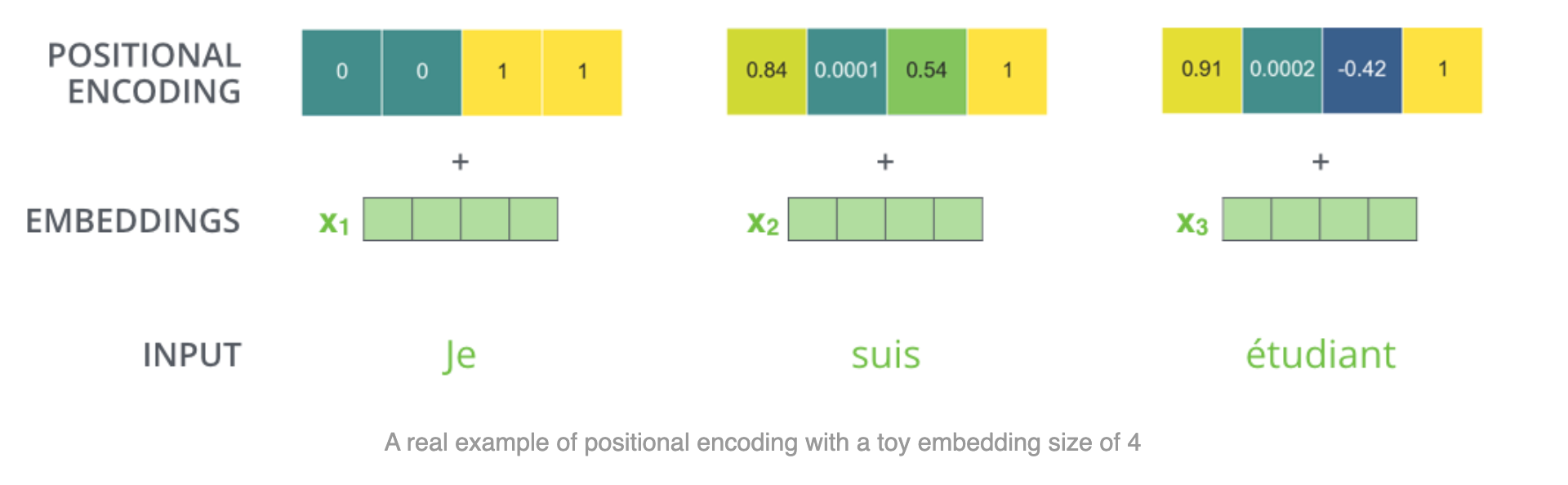
论文中对该嵌入方法生成的 embdding 进行了可视化，如下图所示：

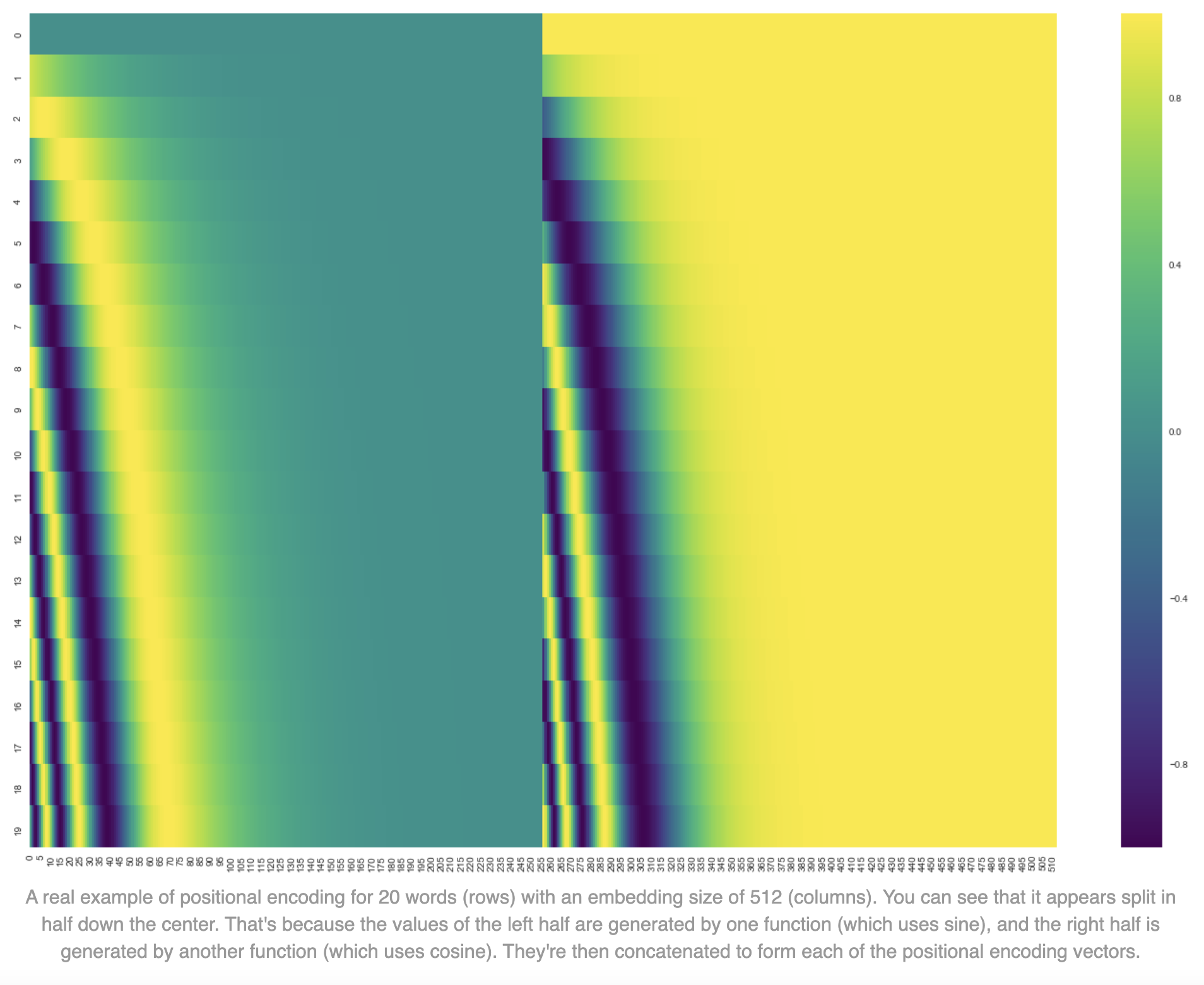
为何如此设计呢？从公式看，sin & cos 的交替使用只是为了使编码更丰富，在哪些维度上使用 sin，哪些使用 cos，不是很重要，都是模型可以调整适应的。而论文给的解释是：

对任意确定的偏移 k，$PE{pos+k}$ 可以表示为 $PE{pos}$ 的函数。

推导的结果是:

$$PE(pos + k, 2i) = PE(pos, 2i) * constant^k_{2i + 1} + constant^k_i * PE(pos, 2i + 1)$$

需要指出的是：

1. 这个函数形式很可能是基于经验得到的，并且应该有不少可以替代的方法；
2. 谷歌后期的作品 BERT 已经换用位置嵌入(positional embedding)来学习了。

3.3 Multi Head Attention

3.3.1 机制概述

多头注意力机制是 Transformer 的核心，且这里的 Attention 被称为 self-attention，是为了区别另一种 target-attention。名字不是特别重要，重点是理解逻辑和实现。这里先抛出对此的看法：模型在理解句中某个词的时候，需要结合上下文，而 Multihead Attention 便是用来从不同角度度量句中单个词与上下文各个词之间关联性的机制。

文字可能没有图片直观，这里以一个可视化的例子来呈现：

如上图所示，当模型想要理解句子 “The animal didn’t cross the street because it was too tired” 中 it 含义的时候，attention 机制可以计算上下文中各个词与它的相关性，图中颜色的深浅便代表相关性大小。

所以，Multihead Attention 模块的任务就是将原本独立的词向量（维度d_k）经过一系列的计算过程，最终映射到一组新的向量(维度d_v)，新向量包含了上下文、位置等有助于词义理解的信息。

3.3.2 Q、K、V变换

模型 Multihead Attention 模块的输入是 embedding 后的一串词向量，而 Attention 机制中原始是对 Query 计算与 Key 的 Weight 后，叠加 Value 计算加权和，所以需要 $Query,Key,Value$ 三个矩阵。

作者便基于 Input 矩阵，通过矩阵变换来生成 Q、K、V，如下图所示，由于 Query 和 Key、Value 来源于同一个Input，故这种机制也称为 self-attention。

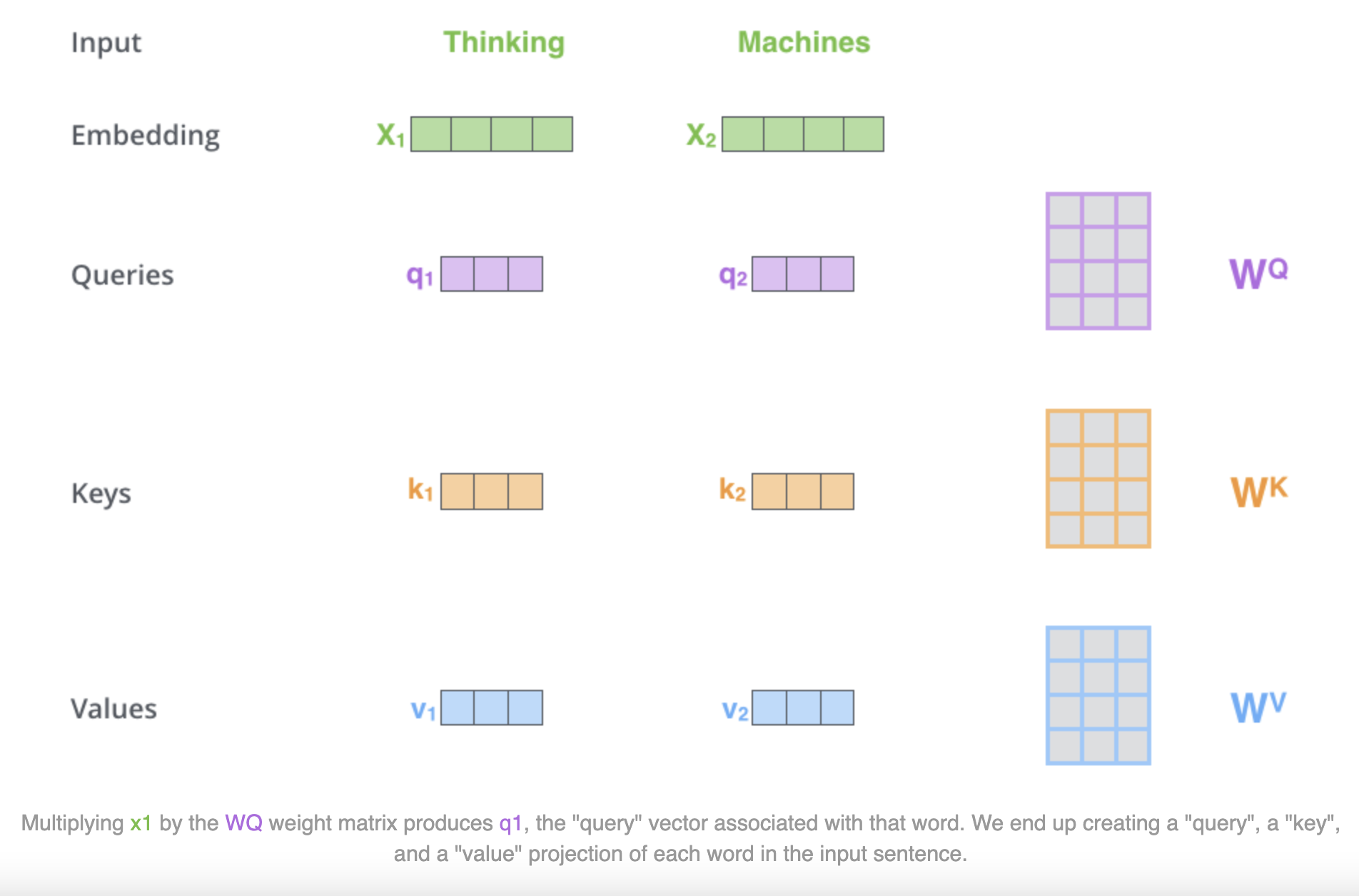
如上图所示，假设 Input 是“Thinking Matchines”句子，只有2个词向量。假设每个词映射为图中的 $1 \times 4$ 的词向量，当我们使用图中所示的3个变换矩阵 $W^Q,W^K,W^V$ 来对 Input 进行变换 (即 $W \times X$) 后，便可以得到变换后的$Q,K,V$矩阵，即每个词向量转换成图中维度为 $1 \times 3$ 的 $q,k,v$。

注意：这些新向量的维度比输入词向量的维度要小（原文 nlp 任务是 512–>64，图中 case 是4->3），并不是必须要小的，是为了让多头 attention 的计算更稳定。

对应的 code 如下所示，其中有一个 Split and concat 模块，这一块本节未提及，是模型中 multi-head 机制的体现，在后文将会详细介绍。

def multihead_attention(queries, keys, values, key_masks,
                        num_heads=8, 
                        dropout_rate=0,
                        training=True,
                        causality=False,
                        scope="multihead_attention"):
    '''Applies multihead attention. See 3.2.2
    queries: A 3d tensor with shape of [N, T_q, d_model].
    keys: A 3d tensor with shape of [N, T_k, d_model].
    values: A 3d tensor with shape of [N, T_k, d_model].
    key_masks: A 2d tensor with shape of [N, key_seqlen]
    num_heads: An int. Number of heads.
    dropout_rate: A floating point number.
    training: Boolean. Controller of mechanism for dropout.
    causality: Boolean. If true, units that reference the future are masked.
    scope: Optional scope for `variable_scope`.
        
    Returns
      A 3d tensor with shape of (N, T_q, C)  
    '''
    d_model = queries.get_shape().as_list()[-1]    # 获取词向量长度
    with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
        # Linear projections    # 通过权重矩阵得出Q,K,V矩阵
        Q = tf.layers.dense(queries, d_model, use_bias=True) # (N, T_q, d_model)
        K = tf.layers.dense(keys, d_model, use_bias=True) # (N, T_k, d_model)
        V = tf.layers.dense(values, d_model, use_bias=True) # (N, T_k, d_model)
        
        # Split and concat    针对最后一个维度划分为多头，词向量长度512 → 每个头64
        Q_ = tf.concat(tf.split(Q, num_heads, axis=2), axis=0) # (h*N, T_q, d_model/h)
        K_ = tf.concat(tf.split(K, num_heads, axis=2), axis=0) # (h*N, T_k, d_model/h)
        V_ = tf.concat(tf.split(V, num_heads, axis=2), axis=0) # (h*N, T_k, d_model/h)
 
        # Attention 计算自注意力
        outputs = scaled_dot_product_attention(Q_, K_, V_, key_masks, causality, dropout_rate, training)
 
        # Restore shape 合并多头
        outputs = tf.concat(tf.split(outputs, num_heads, axis=0), axis=2 ) # (N, T_q, d_model)
              
        # Residual connection 残差链接
        outputs += queries 
              
        # Layer Normalize 
        outputs = ln(outputs)
 
    return outputs

3.3.3 Attention

在文中的全称是 scaled_dot_product_attention（缩放的点积注意力机制），这也是 Transformer 的计算核心。

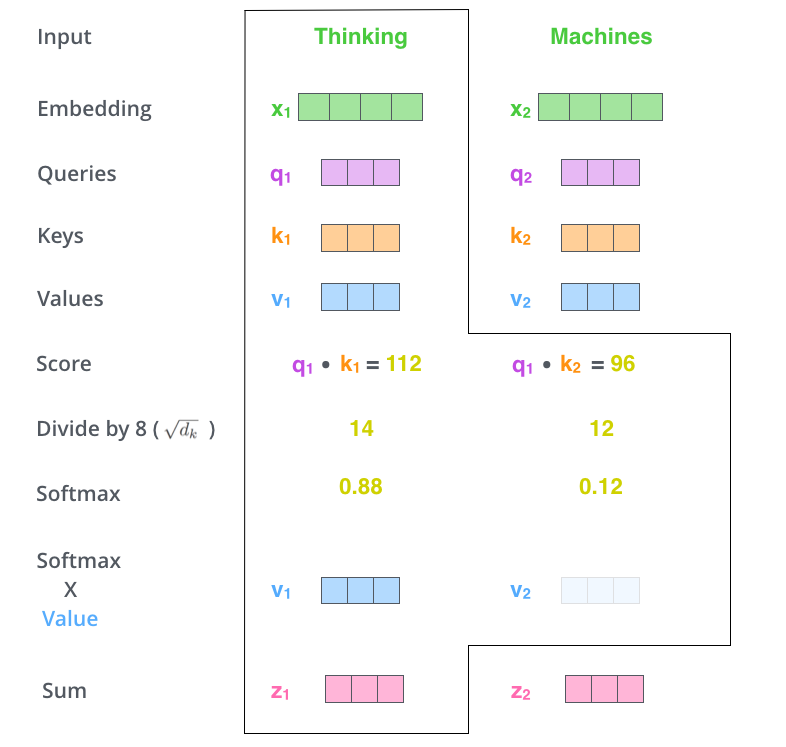
如上图所示，是 Attention 机制的一个计算过程示例。输入有2个词向量($x_1,x_2$)，分别映射成了对应的$q,k,v$向量。

作为 scaled_dot_product_attention 的输入后需要经过如下几步：

1. 计算每组 q, k 的点积，即图中的 Score；
2. 对点积 Score 进行缩放（scaled），即图中的“除以8“，8由$\sqrt{d_k}$计算得到；
3. 基于每个词维度，对其下所有的 scaled Score 计算 Softmax 得到对应的权重 Weight；
4. 用3中的权重对所有向量 $v_i$ 做加权求和，得到最终的 Sum 向量作为 output。

这里需要注意，在第 2 步中对点积的结果 Score 做了 scaled 的原因：

作者提到，这样梯度会更稳定。然后加上softmax操作，归一化分值使得全为正数且加和为1。

后半部分比较好理解，前半部分的原因可从如下角度考虑：假设 Q 和 K 的均值为0，方差为1，它们的矩阵乘积将有均值为0，方差为 $d_k$。因此，$d_k$ 的平方根被用于缩放（而非其他数值）后，因为，乘积的结果就变成了 0 均值和单位方差，这样会获得一个更平缓的 softmax，也即梯度更稳定不容易出现梯度消失。

以上是单个词向量在 Attention 中的计算过程，自然的，多个词向量可以叠加后进行矩阵运算，如下所示。实际上，就是将原来的单词向量$x_i$ ($1 \times d_k$)　堆叠到一起 $X$($N \times d_k$) 进行计算。

输入 $X$ 到 $Q,K,V$ 的矩阵变换过程：

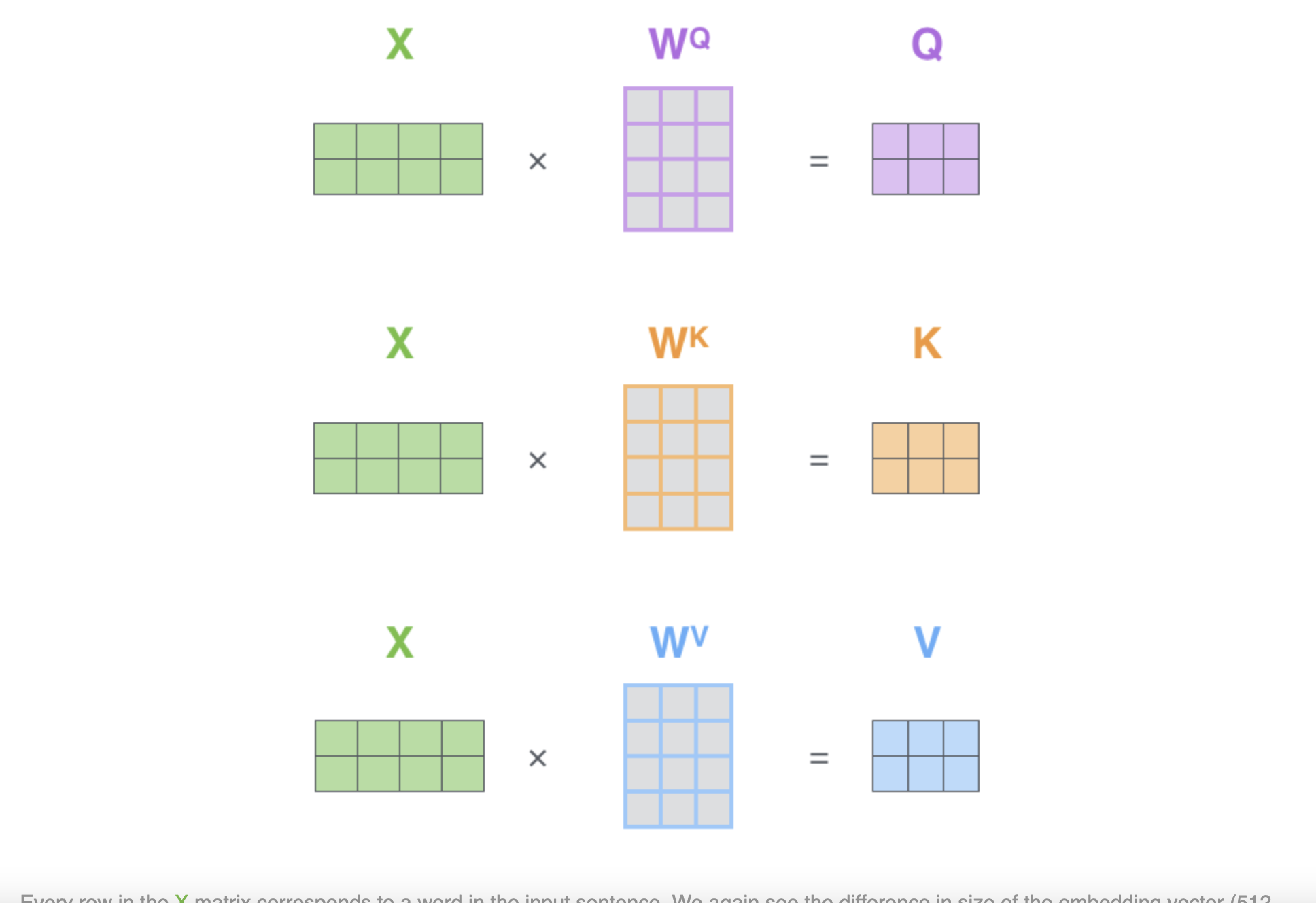
基于$Q,K,V$的 Attention 计算过程：

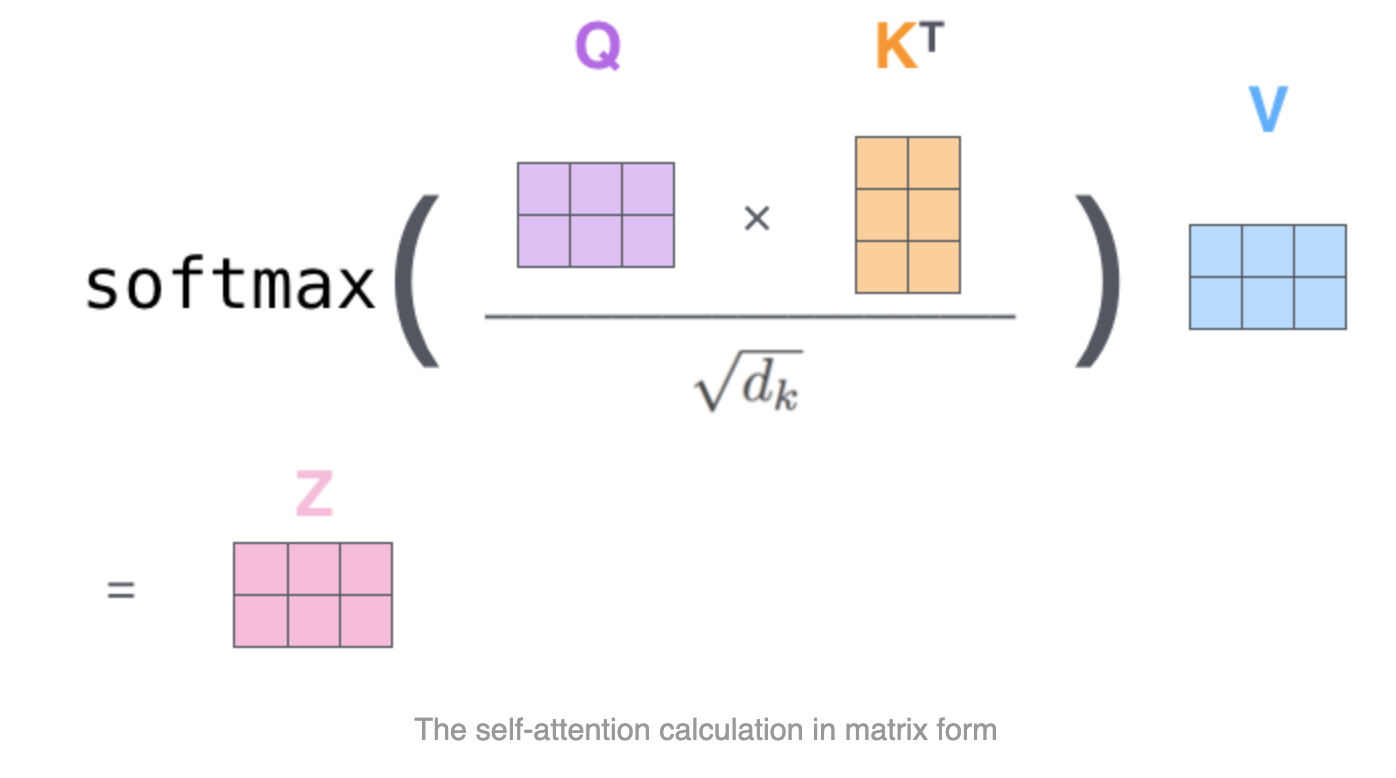
3.3.4 Multi-head

截止上述基本上就是 self-attention 的计算流程了，那么 Multi Attention 中的 multi 就体现在本节的 Multi-head 环节。

我们先看做法：

使用多组 $W^Q,W^K,W^V$ 矩阵进行变换后进行 Attention 机制的计算，如此便可以得到多组输出向量 $Z$，整个流程如下所示。

基于多组 $W^Q,W^K,W^V$ 矩阵映射成多组 $Q,K,V$：

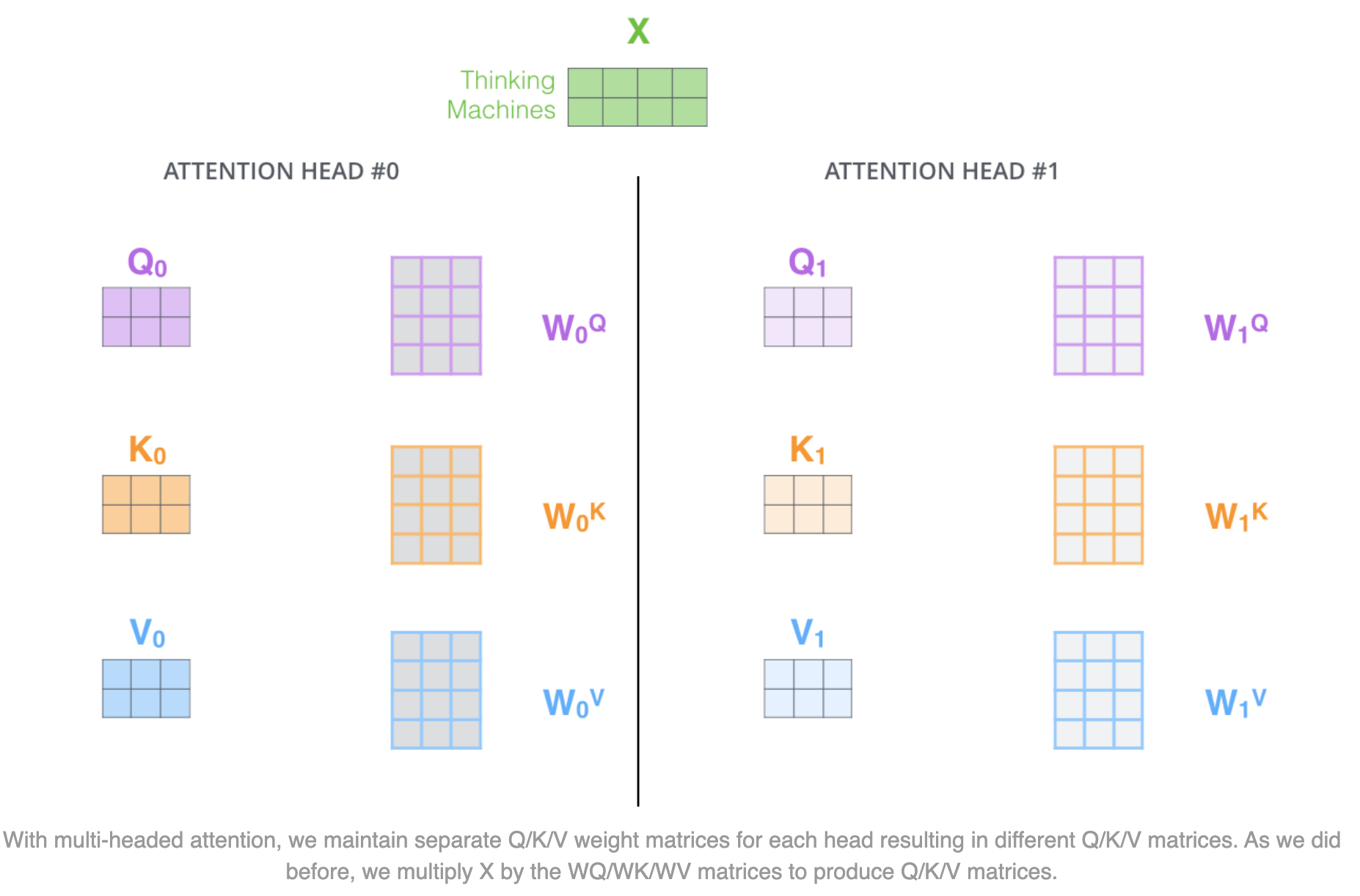
经过 Attention 多组 $Q,K,V$ 得到多个输出矩阵$Z$：

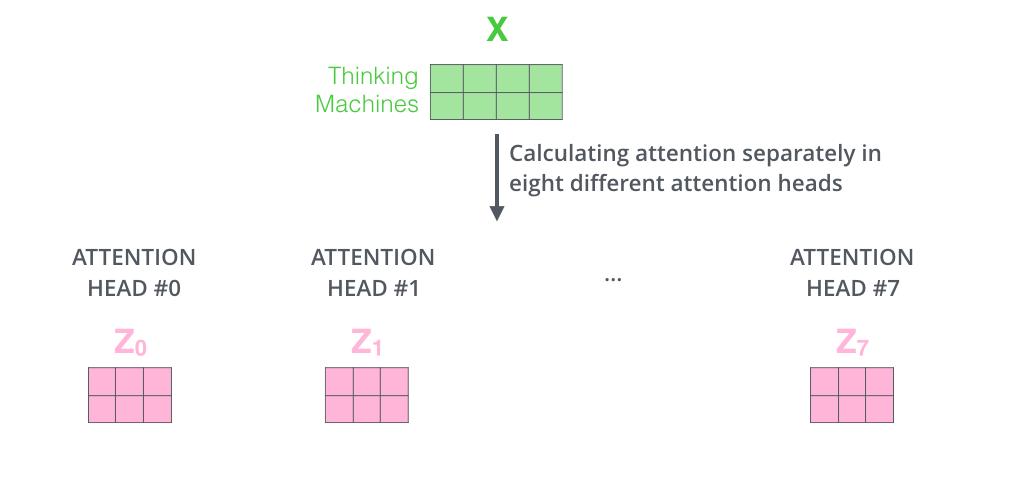
多个输出矩阵$Z$进行 concat 后再线性变换成等嵌入维度($d_k$)的最终输出矩阵$Z$：

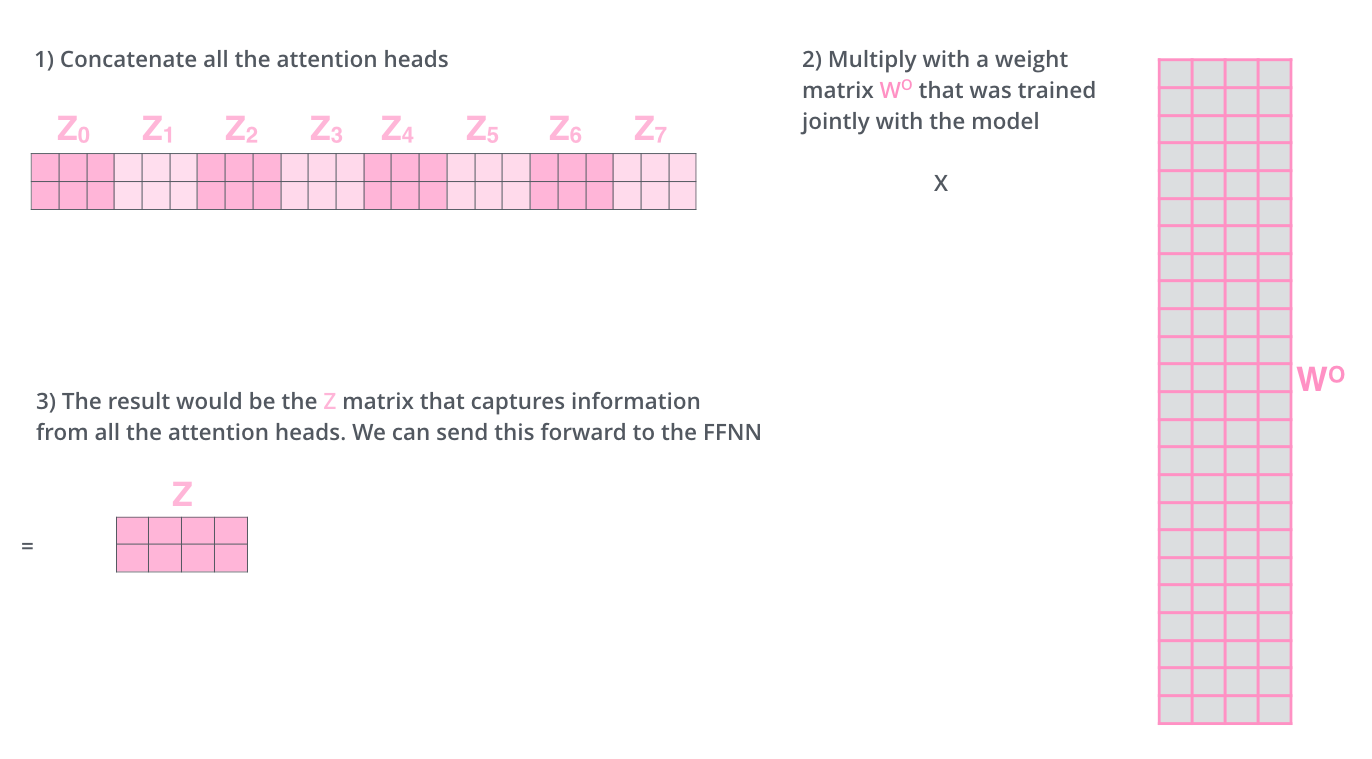
3.3.5 Attention 机制总结

这里直接看整体流程图：

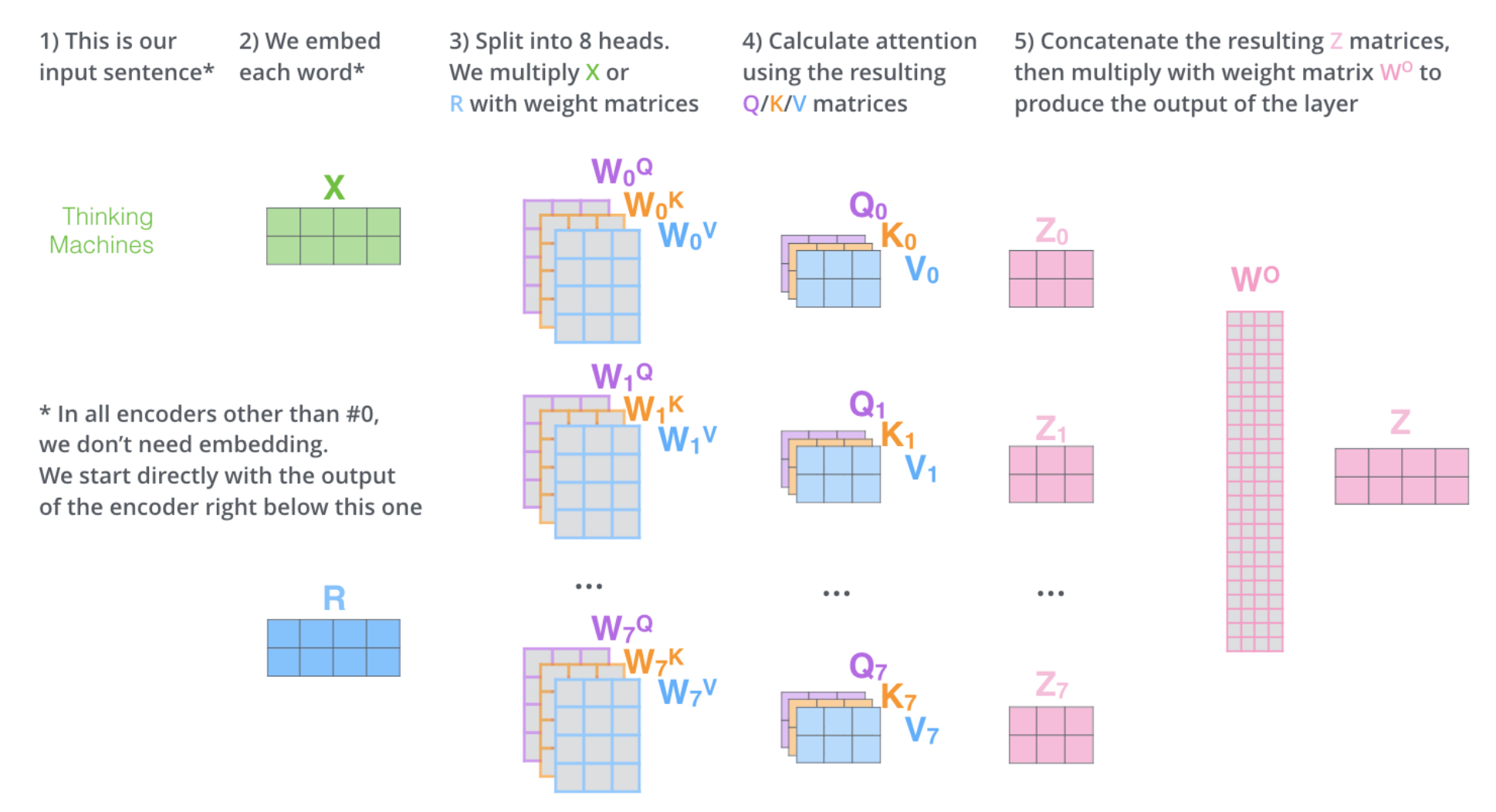
如上图所示，是一个从左往右的计算流程：

1. 输入的句子，这里 case 是”Thinking Machines”;
2. 词嵌入，将词嵌入为 embedding， 其中 R 表示非第 0 个 encoder 的 input 不需要词嵌入，而是上一个 encoder 的 ouput；
3. 生成多组变换权重矩阵；
4. 基于多组权重矩阵（多头）变换映射，得到多组 Q,K,V；
5. 多组 Q,K,V 经过 Attention 后得到多个输出 z，将他们 concat 后进行线性变换得到最终的输出矩阵 Z。

至于为什么要用 Multi Head Attention ？作者提到：

1. 多头机制扩展了模型集中于不同位置的能力。
2. 多头机制赋予 attention 多种子表达方式。

该模块的 code 如下所示，其中还有 mask 和 dropout 模块，前者是为了去除输入中 padding 的影响，后者则是为了提高模型稳健性。后者不过多介绍，mask 的 code 也附在了下方。

方法就是使用一个很小的值，对指定位置进行覆盖填充。在之后计算 softmax 时，由于我们填充的值很小，所以计算出的概率也会很小，基本就忽略了。

值得留意的是：

• type in ("k", "key", "keys"): 是 padding mask，因此全零的部分我们让 attention 的权重为一个很小的值 -4.2949673e+09。
• type in ("q", "query", "queries"): 类似的，query 序列最后面也有可能是一堆 padding，不过对 queries 做 padding mask 不需要把 padding 加上一个很小的值，只要将其置零就行，因为 outputs 是先 key mask，再经过 softmax，再进行 query mask的。
• type in ("f", "future", "right"): 是我们在做 decoder 的 self attention 时要用到的 sequence mask，也就是说在每一步，第 i 个 token 关注到的 attention 只有可能是在第 i 个单词之前的单词，因为它按理来说，看不到后面的单词, 作者用一个下三角矩阵来完成这个操作。

def scaled_dot_product_attention(Q, K, V, key_masks,
                                 causality=False, dropout_rate=0.,
                                 training=True,
                                 scope="scaled_dot_product_attention"):
    '''See 3.2.1.
    Q: Packed queries. 3d tensor. [N, T_q, d_k].
    K: Packed keys. 3d tensor. [N, T_k, d_k].
    V: Packed values. 3d tensor. [N, T_k, d_v].
    key_masks: A 2d tensor with shape of [N, key_seqlen]
    causality: If True, applies masking for future blinding
    dropout_rate: A floating point number of [0, 1].
    training: boolean for controlling droput
    scope: Optional scope for `variable_scope`.
    '''
    with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
        d_k = Q.get_shape().as_list()[-1]
 
        # dot product
        outputs = tf.matmul(Q, tf.transpose(K, [0, 2, 1]))  # (N, T_q, T_k)
 
        # scale
        outputs /= d_k ** 0.5
 
        # key masking
        outputs = mask(outputs, key_masks=key_masks, type="key")
 
        # causality or future blinding masking
        if causality:
            outputs = mask(outputs, type="future")
 
        # softmax
        outputs = tf.nn.softmax(outputs)
        attention = tf.transpose(outputs, [0, 2, 1])
        tf.summary.image("attention", tf.expand_dims(attention[:1], -1))
 
        # # query masking
        # outputs = mask(outputs, Q, K, type="query")
 
        # dropout
        outputs = tf.layers.dropout(outputs, rate=dropout_rate, training=training)
 
        # weighted sum (context vectors)
        outputs = tf.matmul(outputs, V)  # (N, T_q, d_v)
 
    return outputs
    
def mask(inputs, key_masks=None, type=None):
    """Masks paddings on keys or queries to inputs
    inputs: 3d tensor. (h*N, T_q, T_k)
    key_masks: 3d tensor. (N, 1, T_k)
    type: string. "key" | "future" 
    e.g.,
    >> inputs = tf.zeros([2, 2, 3], dtype=tf.float32)
    >> key_masks = tf.constant([[0., 0., 1.],
                                [0., 1., 1.]])
    >> mask(inputs, key_masks=key_masks, type="key")
    array([[[ 0.0000000e+00,  0.0000000e+00, -4.2949673e+09],
        [ 0.0000000e+00,  0.0000000e+00, -4.2949673e+09]],
       [[ 0.0000000e+00, -4.2949673e+09, -4.2949673e+09],
        [ 0.0000000e+00, -4.2949673e+09, -4.2949673e+09]],
       [[ 0.0000000e+00,  0.0000000e+00, -4.2949673e+09],
        [ 0.0000000e+00,  0.0000000e+00, -4.2949673e+09]],
       [[ 0.0000000e+00, -4.2949673e+09, -4.2949673e+09],
        [ 0.0000000e+00, -4.2949673e+09, -4.2949673e+09]]], dtype=float32)
    """
    padding_num = -2 ** 32 + 1 #足够小的负数，保证被填充的位置进入softmax之后概率接近0
    if type in ("k", "key", "keys"): # padding mask
        key_masks = tf.to_float(key_masks)
        key_masks = tf.tile(key_masks, [tf.shape(inputs)[0] // tf.shape(key_masks)[0], 1]) # (h*N, seqlen)
        key_masks = tf.expand_dims(key_masks, 1)  # (h*N, 1, seqlen)
        outputs = inputs + key_masks * padding_num
    # elif type in ("q", "query", "queries"):
    #     # Generate masks
    #     masks = tf.sign(tf.reduce_sum(tf.abs(queries), axis=-1))  # (N, T_q)
    #     masks = tf.expand_dims(masks, -1)  # (N, T_q, 1)
    #     masks = tf.tile(masks, [1, 1, tf.shape(keys)[1]])  # (N, T_q, T_k)
    #
    #     # Apply masks to inputs
    #     outputs = inputs*masks
    elif type in ("f", "future", "right"):    # future mask
        diag_vals = tf.ones_like(inputs[0, :, :])  # (T_q, T_k)    
        tril = tf.linalg.LinearOperatorLowerTriangular(diag_vals).to_dense()  # (T_q, T_k)    # 上三角皆为0
        future_masks = tf.tile(tf.expand_dims(tril, 0), [tf.shape(inputs)[0], 1, 1])  # (N, T_q, T_k)    # N batch size
 
        paddings = tf.ones_like(future_masks) * padding_num
        outputs = tf.where(tf.equal(future_masks, 0), paddings, inputs)     # 上三角中用padding值代替 
    else:
        print("Check if you entered type correctly!")
 
    return outputs

3.4 Add & Norm

在 multihead_attention 模块的代码中有以下2行代码，这边对应着模型结构图 encoder 中的 Add & Norm 模块，如下图所示。

# Residual connection
outputs += queries 

# Layer Normalize 
outputs = ln(outputs)

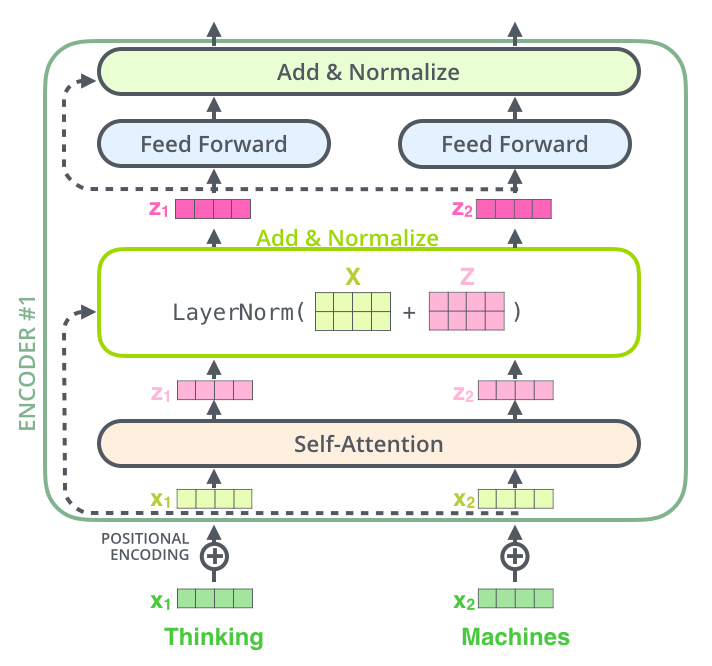
其中 Add 是类似残差的操作，但与残差不同的是，不是用输入减去输出，而是用输入加上输出。

而对于 Norm，这里则用的是 Layer Norm，其代码如后文所示。不论是哪一种实际上都是对输入的分布进行调整，调整的通常方式是：

$$Norm(x_i) = \alpha \times \frac{x_i - u}{\sqrt{\sigma^2_L + \epsilon}} + \beta$$

其中，不同的 Norm 方法便对应着不同的 $u,\sigma$ 计算方式。

这里之所以使用 Layer Norm 而不是 Batch Norm 的原因是：

1. BN 比较依赖 BatchSize，偏小不适合，过大耗费 GPU 显存；
2. BN 需要 batch 内 features 的维度一致；
3. BN 只在训练的时候用，inference 的时候不会用到，因为 inference 的输入不是批量输入；
4. 每条样本的 token 是同一类型特征，LN 擅长处理，与其他样本不关联，通信成本更少；
5. embedding 和 layer size 大，且长度不统一，LN 可以处理且保持分布稳定。

def ln(inputs, epsilon = 1e-8, scope="ln"):
    '''Applies layer normalization. See https://arxiv.org/abs/1607.06450.
    inputs: A tensor with 2 or more dimensions, where the first dimension has `batch_size`.
    epsilon: A floating number. A very small number for preventing ZeroDivision Error.
    scope: Optional scope for `variable_scope`.
      
    Returns:
      A tensor with the same shape and data dtype as `inputs`.
    '''
    with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
        inputs_shape = inputs.get_shape()    # 输入形状
        params_shape = inputs_shape[-1:]    # 
    
        mean, variance = tf.nn.moments(inputs, [-1], keep_dims=True)    # 求均值和方差
        beta= tf.get_variable("beta", params_shape, initializer=tf.zeros_initializer())
        gamma = tf.get_variable("gamma", params_shape, initializer=tf.ones_initializer())
        normalized = (inputs - mean) / ( (variance + epsilon) ** (.5) )
        outputs = gamma * normalized + beta
        
    return outputs

3.5 Feed Forward

承接上述，encoder 中只剩下最后一个环节了，也就是 ff 层（Feed Forward），对比模型图，实际上 ff 后还有一层 Add & Norm，但是一般将其二者合并在一个模块中，统称为 ff 层。

该模块的 code 如下所示，相对比较清晰，2 层 dense 网络后紧接一个 Residual connection 即将输入直接相加，最后再过一层 Layer Normalization 即可。

def ff(inputs, num_units, scope="positionwise_feedforward"):
    '''position-wise feed forward net. See 3.3
    
    inputs: A 3d tensor with shape of [N, T, C].
    num_units: A list of two integers.  
                num_units[0]=d_ff: 隐藏层大小（2048）
                num_units[1]=d_model: 词向量长度（512）
    scope: Optional scope for `variable_scope`.
    Returns:
      A 3d tensor with the same shape and dtype as inputs
    '''
    with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
        # Inner layer
        outputs = tf.layers.dense(inputs, num_units[0], activation=tf.nn.relu)
 
        # Outer layer 
        outputs = tf.layers.dense(outputs, num_units[1])
 
        # Residual connection
        outputs += inputs
        
        # Layer Normalize
        outputs = ln(outputs)
    
    return outputs

3.6 decoder

截止上述是完成了模型的 encoder 模块，本节重点介绍 decoder 模块，其在应用形式上与 encoder 略有不同，整体结构如前文模型结构图中已有展示，容易发现有几个特殊之处：

1. 输入是经过 Sequence Mask 的，也就是掩去未出现的词；
2. 每个 decoder 有 2 个 multihead_attention 层；
3. 首层 multihead_attention 的 $Q,K,V$都是来源输入向量，第二层输入中的 $K,V$ 则是来自 encoder 模块的输出作为 memory 来输入。

整个 decoder 侧的工作原理可以如下动画展示：

其中在最后一层 Linear+Softmax 后是怎么得到单词的，想必了解 nlp 的同学也不会陌生，一般就是转化为对应词表大小的概率分布，取最大的位置词即可，如下图所示：

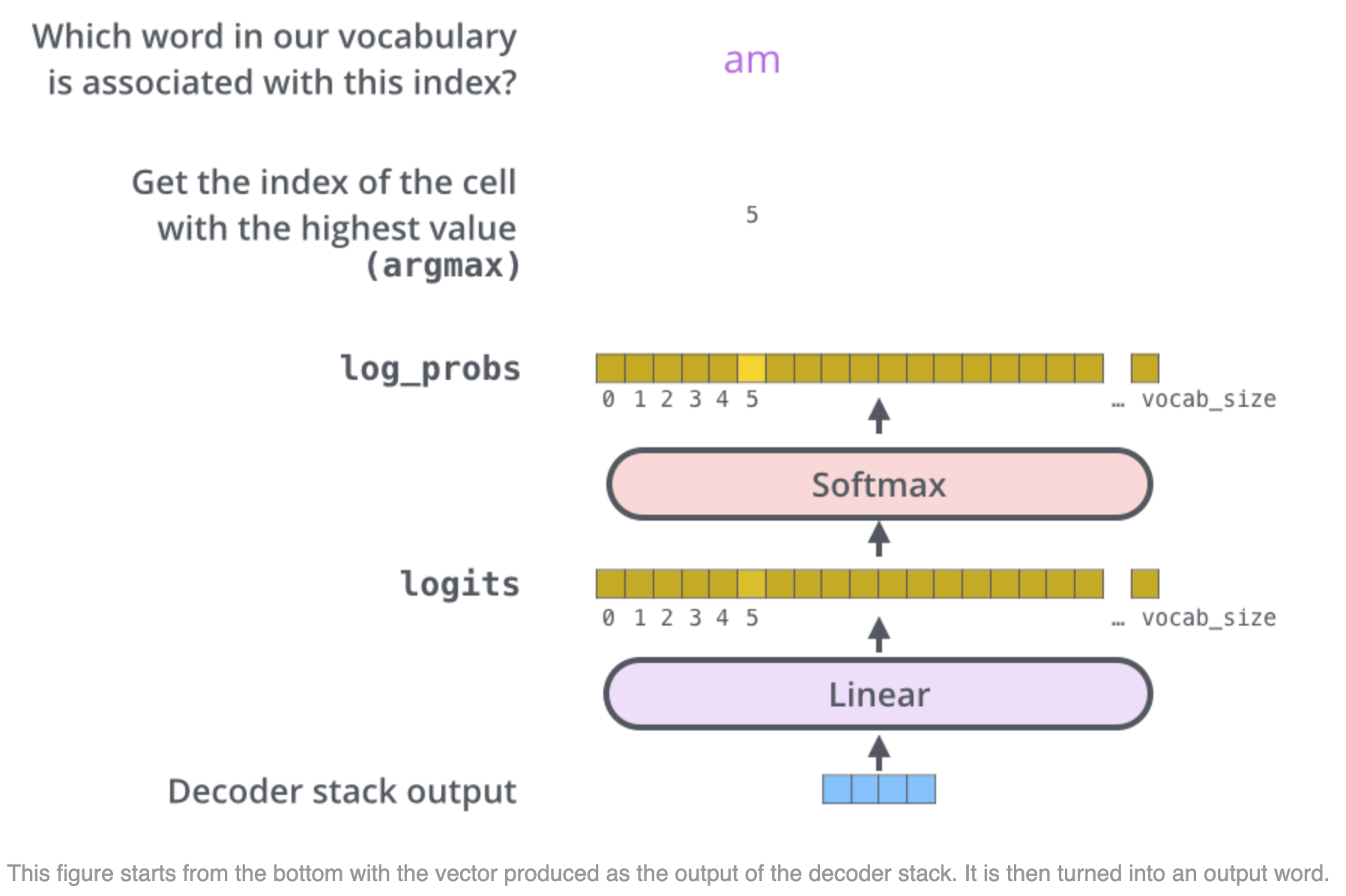
整个 decode 的 code 如下所示，可以清晰的看到 decoder 前的处理与 encoder 几乎一致，唯独 mask 模块走的是 Sequence Mask，在前面的 mask 代码有涉及。每个 decoder 中的 2 层 multihead_attention 的输入差异也比较清晰，重点就是将 encode 模块的输出应用在每个 decoder 的第二层 multihead_attention 中。输出的时候，实际上利用了 softmax 的单调性，直接使用 tf.argmax 来获取最大值位置。

def decode(self, ys, memory, src_masks, training=True):
    '''
    memory: encoder outputs. (N, T1, d_model)
    src_masks: (N, T1)

    Returns
    logits: (N, T2, V). float32.
    y_hat: (N, T2). int32
    y: (N, T2). int32
    sents2: (N,). string.
    '''
    with tf.variable_scope("decoder", reuse=tf.AUTO_REUSE):
        decoder_inputs, y, seqlens, sents2 = ys

        # tgt_masks
        tgt_masks = tf.math.equal(decoder_inputs, 0)  # (N, T2)

        # embedding
        dec = tf.nn.embedding_lookup(self.embeddings, decoder_inputs)  # (N, T2, d_model)
        dec *= self.hp.d_model ** 0.5  # scale

        dec += positional_encoding(dec, self.hp.maxlen2)
        dec = tf.layers.dropout(dec, self.hp.dropout_rate, training=training)

        # Blocks
        for i in range(self.hp.num_blocks):
            with tf.variable_scope("num_blocks_{}".format(i), reuse=tf.AUTO_REUSE):
                # Masked self-attention (Note that causality is True at this time)
                dec = multihead_attention(queries=dec,
                                          keys=dec,
                                          values=dec,
                                          key_masks=tgt_masks,
                                          num_heads=self.hp.num_heads,
                                          dropout_rate=self.hp.dropout_rate,
                                          training=training,
                                          causality=True,
                                          scope="self_attention")

                # Vanilla attention
                dec = multihead_attention(queries=dec,
                                          keys=memory,
                                          values=memory,
                                          key_masks=src_masks,
                                          num_heads=self.hp.num_heads,
                                          dropout_rate=self.hp.dropout_rate,
                                          training=training,
                                          causality=False,
                                          scope="vanilla_attention")
                ### Feed Forward
                dec = ff(dec, num_units=[self.hp.d_ff, self.hp.d_model])

    # Final linear projection (embedding weights are shared)
    weights = tf.transpose(self.embeddings) # (d_model, vocab_size)
    logits = tf.einsum('ntd,dk->ntk', dec, weights) # (N, T2, vocab_size)
    y_hat = tf.to_int32(tf.argmax(logits, axis=-1))

    return logits, y_hat, y, sents2

3.7 特殊模块

3.7.1 label_smoothing

如前文提到的 train 模块代码，在 decode 后，紧接的便是 label_smoothing 模块。其作用就是：

平滑一下标签值，比如 ground truth 标签是 1 的，改到 0.9333，本来是 0 的，他改到 0.0333，这是一个比较经典的平滑技术了。

def label_smoothing(inputs, epsilon=0.1):
    '''Applies label smoothing. See 5.4 and https://arxiv.org/abs/1512.00567.
    inputs: 3d tensor. [N, T, V], where V is the number of vocabulary.
    epsilon: Smoothing rate.
    
    For example,
    

import tensorflow as tf
inputs = tf.convert_to_tensor([[[0, 0, 1], 
   [0, 1, 0],
   [1, 0, 0]],

  [[1, 0, 0],
   [1, 0, 0],
   [0, 1, 0]]], tf.float32)

outputs = label_smoothing(inputs)

with tf.Session() as sess:
    print(sess.run([outputs]))

>>
[array([[[ 0.03333334,  0.03333334,  0.93333334],
    [ 0.03333334,  0.93333334,  0.03333334],
    [ 0.93333334,  0.03333334,  0.03333334]],

   [[ 0.93333334,  0.03333334,  0.03333334],
    [ 0.93333334,  0.03333334,  0.03333334],
    [ 0.03333334,  0.93333334,  0.03333334]]], dtype=float32)]   
'''
V = inputs.get_shape().as_list()[-1] # number of channels
return ((1-epsilon) * inputs) + (epsilon / V)

3.7.2 noam_scheme

在模型的学习了上，作者使用了 noam_scheme 这样一个机制来处理。代码如后文所示，使用的学习率递减公式为：

$$Lr = init_lr * warm_step^{0.5} * min(s * warm_step^{-1.5}, s^{-0.5})$$

其中，$init_lr$ 是指初始学习率，$warm_step$ 是指预热步数，而 $s$ 则是代表全局步数。

def noam_scheme(init_lr, global_step, warmup_steps=4000.):
    '''Noam scheme learning rate decay
    init_lr: initial learning rate. scalar.
    global_step: scalar.
    warmup_steps: scalar. During warmup_steps, learning rate increases
        until it reaches init_lr.
    '''
    step = tf.cast(global_step + 1, dtype=tf.float32)
    return init_lr * warmup_steps ** 0.5 * tf.minimum(step * warmup_steps ** -1.5, step ** -0.5)

3.8 其他

3.8.1 项目运行

该项目运行需要 sentencepiece，其安装的时候留意是否关了 VPN，否则安装会失败，然后可以使用如下代码直接安装：

pip install sentencepiece

3.8.2 uitls模块

Transformer 项目中 utils 模块是训练中使用到的工具算子集合，这里简单较少一下各个算子的作用。

• calc_num_batches: 计算样本的 num_batch，就是 total_num/batch_size 取整，再加1；
• convert_idx_to_token_tensor: 将 int32 转为字符串张量（string tensor）;
• postprocess: 做翻译后的处理，输入一个是翻译的预测列表，还有一个是 id2token 的表，就是用查表的方式把数字序列转化成字符序列，从而形成一句可以理解的话。(如果做中文数据这个就要改一下了，中文不适用BPE等word piece算法)。
• save_hparams: 保存超参数。
• load_hparams: 加载超参数并覆写parser对象。
• save_variable_specs: 保存一些变量的信息，包括变量名，shape，总参数量等等。
• get_hypotheses: 得到预测序列。这个方法就是结合前面的 postprocess 方法，来生成 num_samples 个数的有意义的自然语言输出。
• calc_bleu: 计算BLEU值。

3.8.3 data_load模块

在数据加载中有不少预处理环节，我们重点介绍一下相关算子。

• load_vocab: 加载词汇表。参数 vocab_fpath表示词文件的地址，会返回两个字典，一个是 id->token，一个是 token->id；
• load_data: 加载数据。加载源语和目标语数据，筛除过长的数据，注意是筛除，也就是长度超过maxlen的数据直接丢掉了，没加载进去。
• encode: 将字符串转化为数字，这里具体方法是输入的是一个字符序列，然后根据空格切分，然后如果是源语言，则每一句话后面加上“\</s>”，如果是目标语言，则在每一句话前面加上”\“，后面加上“\</s>”，然后再转化成数字序列。如果是中文，这里很显然要改。
• generator_fn: 生成训练和评估集数据。对于每一个sent1，sent2（源句子，目标句子），sent1经过前面的encode函数转化成x，sent2经过前面的encode函数转化成y之后，decoder的输入decoder_input是y[:-1]，预期输出y是y[1:]。
• input_fn: 生成Batch数据。
• get_batch: 获取batch数据。

参考文章
Attention is All You Need
transformer 源码
Transformer和Bert相关知识解
Transformer(二)—论文理解：transformer 结构详解
Python - 安装sentencepiece异常
The Illustrated Transformer【译】
The Illustrated Transformer
Attention专场——（2）Self-Attention 代码解析
如何理解Transformer论文中的positional encoding，和三角函数有什么关系？

---