SNE 和 t-SNE 算法

1 引言

实际研究中有很多的降维算法，例如经典的线性降维算法PCA，相信很多人都比较熟悉了。而在这里，我们要介绍的是一个经典的降维算法t-SNE，它往往用来对高维数据做非线性降维来进行可视化分析。参考了不少大牛的文章，加上一些自己的思考，从一个小白的角度来总结一下该算法的原理和使用姿势。

1.1 维数灾难

维数灾难（curse of dimensionality）：描述的是高维空间中若干迥异于低维空间、甚至反直觉的现象。

在这里我们要阐述两个理论：

高维空间中数据样本极其稀疏。
如下图所示，高维数据降维到低维空间将发生“拥挤问题（Crowding Problem）。

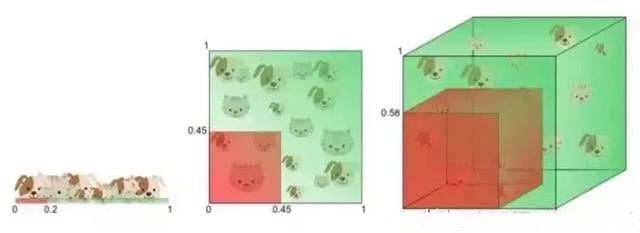
高维单位空间中数据几乎全部位于超立方体的边缘。

1.2 数理佐证

以上两个理论并不是空口而谈，我们能够用几何学来证明。首先，在高维空间中的单位超立方体的体积是：

$V_{hypercube} = 1^d = 1$

对应的内切球体积为：

$V_{hypersphere} = \frac{\pi^{n/2}}{\Gamma(n/2 + 1)} \cdot 0.5^d$

两者的商取极限就有：

$lim_{d \to +\infty} \frac{V_{hypersphere}}{V_{hypercube}} = 0$

上述表明：在极端的高维情况下，单元空间只有边角，而没有中心。数据也只能处于边缘上，而远离中心。

由此我们又能推出结论：欧式距离会失效

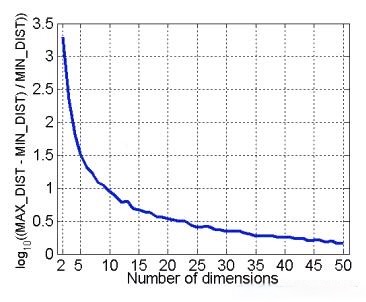
上图描述的是高维空间中大距离和小距离的差异越来越不明显：

$lim_{d \to +\infty} \frac{dist_{max} - dist_{min}}{d_{min}} = 0$

所以降维的基本作用：

缓解维数灾难，使得欧式距离重新生效；
数据预处理，降噪去冗余；
可视化分析。

1.3 SNE算法的思想基础

SNE 的两个思想要点：

构建一个高维对象之间的概率分布，使得对象间的相似度和被选择的概率成正相关；
将高维的数据映射到低维空间，使得两个空间的概率分布尽可能相似；

看下面的图，比较形似。高维空间中的数据点对应低维空间的数据点，通过一个链接关系牵引使得两个空间中对应数据点的分布类似。

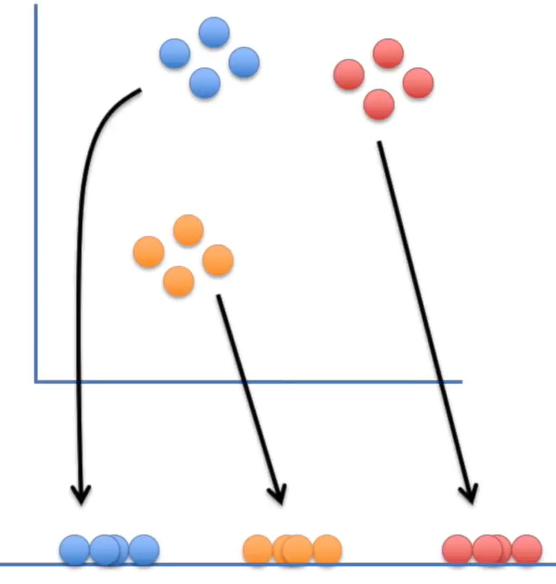
SNE 两个主要步骤：

将欧氏距离转化为条件概率来表征点间相似度（pairwise similarity）。
使用梯度下降算法来使低维分布学习/拟合高维分布。

2 SNE的算法原理

给定一组高维空间的数据样本： $(x_1, … , x_N)$ ，其中N表示的是样本数，并不是维度。前面我们提到，在高维空间中，欧式距离将会失效，所以这里会将其转化成条件概率来度量两个样本数据之间的相似度或者说距离。

2.1 相似性度量-条件概率

那么对于样本点$xi $来说，上面提到的相似性度量$ p{j|i} $就是以高斯分布来选择$ x_j$作为近邻点的条件概率：

$p_{j \mid i} = \frac{\exp(- \mid \mid x_i -x_j \mid \mid ^2 / (2 \sigma^2_i ))} {\sum_{k \neq i} \exp(- \mid \mid x_i - x_k \mid \mid ^2 / (2 \sigma^2_i))}$

这里需要指出三点：

对除 i 外其他所有 j 都计算一个条件概率后，形成一个概率分布列，所以分母需要归一化；
设定 $p_{i|i}=0$ ，因为我们关注的是两两之间的相似度。
有一个参数是 $\sigma_i$ ，对于不同的点 $x_i$ 取值不一样。

另一方面，如前面所述，降维就是将高维映射到低维，那么我们对上述的高维样本点 $(x_1, … , x_N)$ ，构造出低维空间中对应的样本点 $(y_1, … , y_N)$ 。同样的，该空间中也有对应的度量相似度的条件概率：

$q_ {j \mid i} = \frac{\exp(- \mid \mid x_i -x_j \mid \mid ^2)} {\sum_{k \neq i} \exp(- \mid \mid x_i - x_k \mid \mid ^2)}$

注意：这里我们令 $\sigma_i = \frac{1}{\sqrt 2}$ ，若方差取其他值，对结果影响仅仅是缩放而已。

2.2 高低维空间分布一致性

到这里，我们已经定义了原始高维空间的样本数据以及映射到低位空间后的对应数据点，以及两个空间中度量样本相似度的条件概率。基于前文的算法思想：我们需要做的就是让低维空间的数据分布尽可能的靠近或者拟合高维空间中的样本分布。提到度量分布的一致程度，很自然的能够想到KL散度。

$C = \sum_i KL(P_i \mid \mid Q_i) = \sum_i \sum_j p_{j \mid i} \log \frac{p_{j \mid i}}{q_{j \mid i}}$

其中，$Pi(k = j) = p{j|i} $和$ Qi(k = j) = q{j|i} $是两个分布列。所以，我们期望，在降维效果好的时候局部分布保留相似性，即$ p{i|j} = q{i|j}$。

这里需要注意：KL散度具有不对称性。

则如果高维数据相邻而低维数据分开（即p大q小），则cost很大；相反，如果高维数据分开而低维数据相邻（即p小q大），则cost很小。

所以，SNE倾向于保留高维数据的局部结构。

2.3 困惑度(perplexity)

前面的公式中我们提到了不同的点具有不同的 $\sigma_i$ ，而 $P_i$ 的熵会随着 $\sigma_i$ 的增加而增加。

$Perp(P_i) = 2^{H(P_i)} = 2^{-\sum_j p_{j \mid i} \log_2 p_{j \mid i}}$

注意：困惑度设的大，则显然σ_i也大。两者是单调关系，因此可以使用二分查找。

虽然该取值对效果具有一定的鲁棒性，但一般建议困惑度设为5-50比较好，它可以解释为一个点附近的有效近邻点个数。

2.4 梯度求解

前面已经介绍了 lossfunc，简单推导可知其梯度公式为：

$\frac{\partial C}{\partial y_i} = 2 \sum_j (p_{j \mid i} - q_{j \mid i} + p_{i \mid j} - q_{i \mid j})(y_i - y_j)$

其结构与 softmax 类似。我们知道 $\sum -y \log p$ 对应的梯度为 $y-p$ 可以简单推导得知SNE的lossfunc中的i在j下的条件概率情况的梯度是$2(p{i \mid j}-q{i \mid j})(yi-y_j) $，同样j在i下的条件概率的梯度是$ 2(p{j \mid i}-q_{j \mid i})(y_i-y_j)$.

为了加速优化过程和避免陷入局部最优解，我们需要引入动量，即之前的梯度累加的指数衰减项：

$y_i^{(t)} = y_i^{(t-1)} + \eta \frac{\partial C}{\partial y_i} + \alpha(t)(y_i^{(t-1)} - y_i^{(t-2)})$

在初始优化的阶段，每次迭代中可以引入一些高斯噪声，之后像模拟退火一样逐渐减小该噪声，可以用来避免陷入局部最优解。因此，SNE在选择高斯噪声，以及学习速率，什么时候开始衰减，动量选择等等超参数上，需要跑多次优化才可以。

2.5 SNE的问题

虽然上述给出了SNE算法的原理和求解方式，但实际上其是比较难以优化的，而且存在crowding problem(拥挤问题)：

由于降维后的空间压缩，会使得哪怕高维空间中离得较远的点，在低维空间中留不出这么多空间来映射。于是到最后高维空间中的点，尤其是远距离和中等距离的点，在低维空间中统统被塞在了一起。

这里的原理在前文已经详细介绍过，是一个比较重要的问题。所以，Hinton 等人又提出了 t-SNE 的方法。与 SNE 不同，主要如下:

使用对称版的SNE，简化梯度公式
低维空间下，使用t分布替代高斯分布表达两点之间的相似度

3 对称 SNE(Symmetric SNE)

我们首先简单介绍一下对称SNE，它也是一种缓解拥挤问题的办法。它的主要思想就是使用联合概率分布来替换条件概率分布。我们假设P是高维空间里的各个点的联合概率分布，Q是对应的低维空间，目前函数：

$C = KL(P \mid \mid Q) = \sum_i \sum_j p_{i,j} \log \frac{p_{ij}}{q_{ij}}$

这里的$p{ii}, q{ii}$为0，我们将这种SNE称之为 symmetric SNE (对称SNE)，因为他假设了对于任意i,$p{ij} = p{ji}, q{ij} = q{ji}$，因此概率分布可以改写为:

$p_{ij} = \frac{\exp(- \mid \mid x_i - x_j \mid \mid ^2 / 2\sigma^2)}{\sum_{k \neq l} \exp(- \mid \mid x_k-x_l \mid \mid ^2 / 2\sigma^2)} \ \ \ \ q_{ij} = \frac{\exp(- \mid \mid y_i - y_j \mid \mid ^2)}{\sum_{k \neq l} \exp(- \mid \mid y_k-y_l \mid \mid ^2)}$

公式整体简洁一些，但是如果 $x_i$ 是异常值，将会使得 $||x_i - x_j||^2$ 很大，那么对应的lossfunc就会很小，会使得训练不好。为了解决此问题，我们可以将联合概率分布修改为：

$p_{ij} = \frac{p_{i|j} + p_{j|i}}{2}$

如此便可以保证$\sumj p{ij} > \frac{1}{2n}$，即每一个样本都会贡献一定的lossfunc，并且使得梯度变成：

$\frac{\partial C}{\partial y_i} = 4 \sum_j (p_{ij} - q_{ij})(y_i - y_j)$

实际使用中对称SNE往往不会比SNE的效果差。

4 t-SNE算法

4.1 t分布的应用到SNE

上面介绍了SNE的问题和对称SNE，更正统的做法便是t-SNE算法：

在不同空间使用不同的分布来将距离转换成概率分布，高维空间中一般用高斯分布，而在对应的低维空间中我们一般使用更加长尾的t-分布，如此便可以使得高维度下中低等的距离在映射后能够有一个较大的距离。

首先我们知道t-分布的概率密度函数（PDF）形式为：

$f(t) = \frac{\Gamma(\frac{v+1}{2})}{\sqrt{v \pi} \Gamma(\frac{v}{2})} (1 + \frac{t^2}{v})^{-\frac{v+1}{2}}$

其中v代表数据的自由度，当 $v=1$ 的时候一般称为柯西分布（Cauchy distribution），这就是我们在低维空间中将要使用的具体分布：

$f(t) = \frac{1}{\pi(1 + t^2)}$

而当 $v = \infty$ 的时候就称为高斯/正态分布(Guassian/Normal distribution)，也就是原始数据高维空间中使用的分布：

$f(t) = \frac{1}{\sqrt{2 \pi}} e^{- \frac{t^2}{2}}$

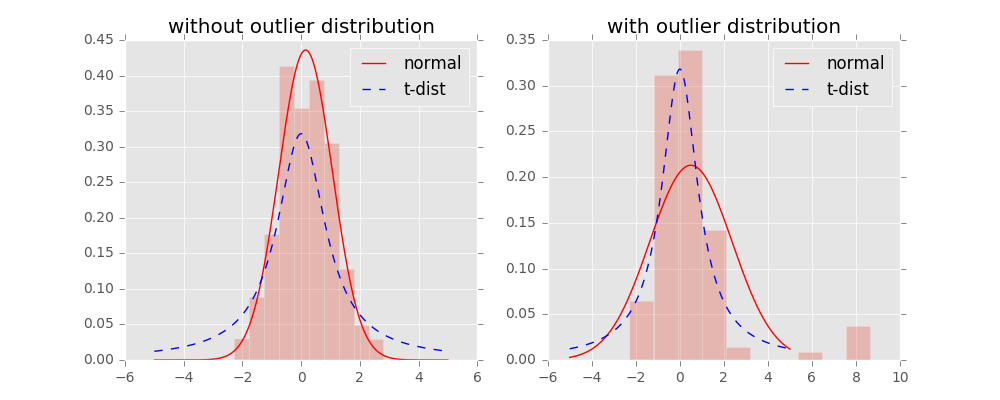
上图展示了所介绍的两个分布的对比图，可以发现t-分布相对厚尾许多，能够更好的捕捉真实数据特征。

回到SNE求解那里，我们使用t-分布带入变换之后，将得到：

$q_{ij} = \frac{(1 + \mid \mid y_i -y_j \mid \mid ^2)^{-1}}{\sum_{k \neq l} (1 + \mid \mid y_i -y_j \mid \mid ^2)^{-1}}$

对应的梯度为：

$\frac{\delta C}{\delta y_i} = 4 \sum_j(p_{ij}-q_{ij})(y_i-y_j)(1+ \mid \mid y_i-y_j \mid \mid ^2)^{-1}$

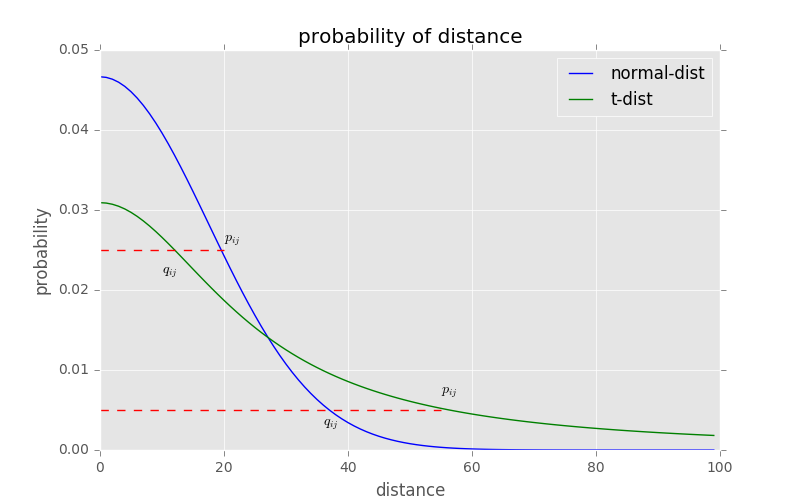
为了更好的展示为什么使用t-分布可以通过“把尾巴抬高”来缓解SNE的拥挤问题，我们将两个分布的映射对比图画出如下所示。其中，横轴表示距离，纵轴表示相似度。我们可以发现t-分布很好的满足了我们的需求，即：

对于较大相似度的点，即图中上方的红线，表明t分布在低维空间中的距离需要稍小一点；
对于低相似度的点，即图中下方的红线，表明t分布在低维空间中的距离需要更远。

4.2 t-SNE缺点

时间、空间复杂度为O(n^2)，计算代价昂贵。百万量级的数据需要几小时，对于PCA可能只需要几分钟。
升级版 Barnes-Hut t-SNE 可以让复杂度降为O(nlogn)，但只限于获得二维和三维的嵌入。（sklearn中可以直接使用参数method=’barnes_hut’）
由于代价函数非凸，多次执行算法的结果是随机的（名字中“Stochatsic”的由来？），需要多次运行选取最好的结果。
全局结构不能很清楚的保留。这个问题可以通过先用PCA降维到一个合理的维度（如50）后再用t-SNE来缓解，前置的PCA步骤也可以起到去除噪声等功能。（sklearn中可以直接使用参数init=’pca’）

4.3 小补充

优化过程中可以尝试的两个 trick:

提前压缩(early compression)：开始初始化的时候，各个点要离得近一点。这样小的距离，方便各个聚类中心的移动。可以通过引入L2正则项(距离的平方和)来实现。
提前夸大(early exaggeration)：在开始优化阶段，pij 乘以一个大于1的数进行扩大，来避免因为 qij 太小导致优化太慢的问题。比如前50次迭代，pij 乘以4。

最后附上一幅常见的t-SNE降维过程效果图：

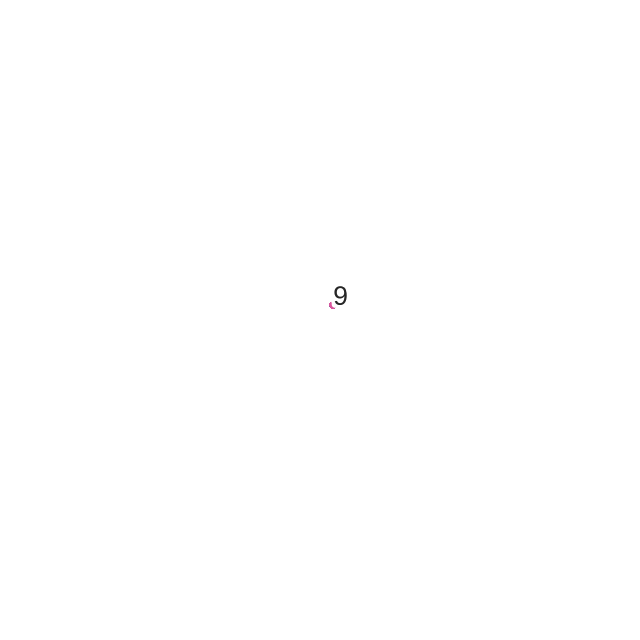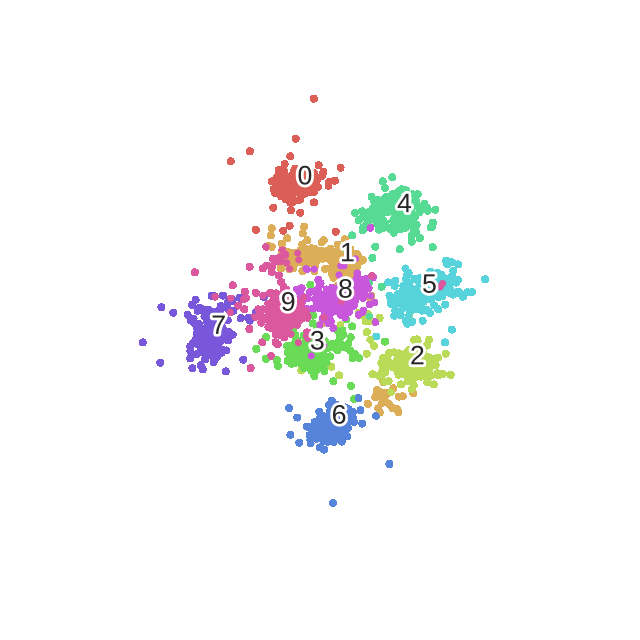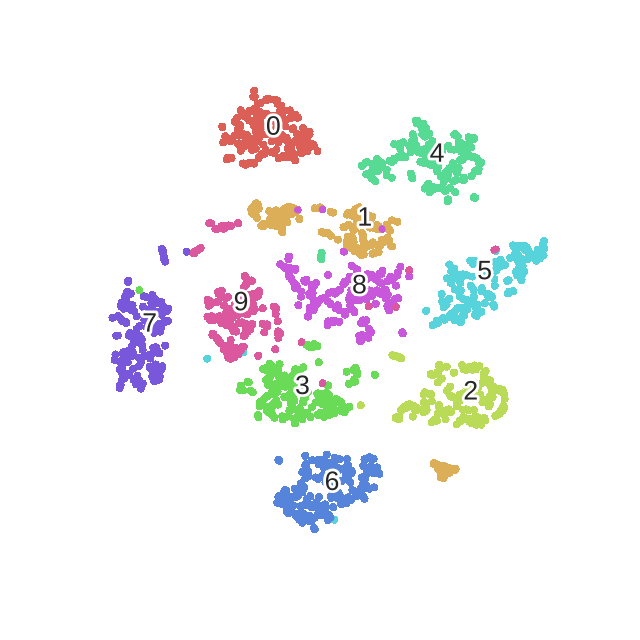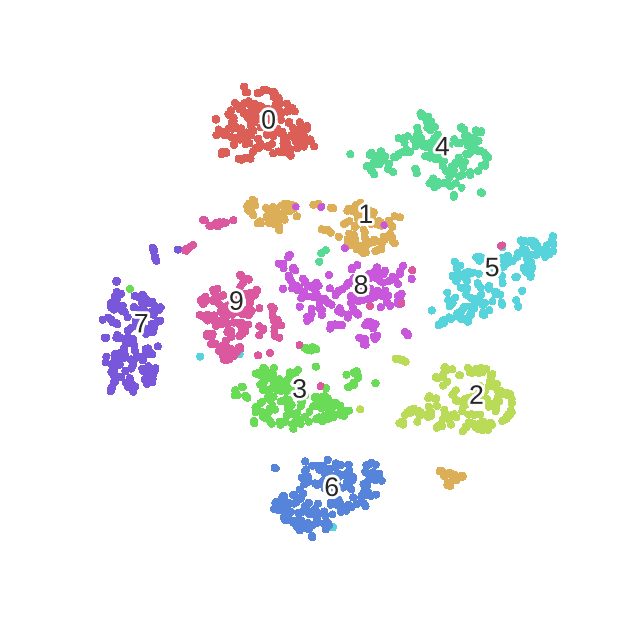
5 t-SNE实战coding

我们来看两个简单的例子。

假设现在有一组3维数据，我需要将其降维到2维进行可视化。

def hello_tSNE():
    X = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
    tsne = TSNE(n_components=2)
    tsne.fit_transform(X)
    print(tsne.embedding_)

高维S曲线数据的降维可视化。

"""
S curve visualization
"""
# # Next line to silence pyflakes. This import is needed.
# Axes3D
def tSNE_forS():
    n_points = 1000
    # 生成S曲线的样本数据
    # X是一个(1000, 3)的2维数据，color是一个(1000,)的1维数据
    X, color = datasets.make_s_curve(n_points, random_state=0)
    n_neighbors = 10
    n_components = 2

    fig = plt.figure(figsize=(8, 8))
    # 创建了一个figure，标题为"Manifold Learning with 1000 points, 10 neighbors"
    plt.suptitle("Manifold Learning with %i points, %i neighbors"
                 % (1000, n_neighbors), fontsize=14)

    '''绘制S曲线的3D图像'''
    ax = fig.add_subplot(211, projection='3d')
    ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
    ax.view_init(4, -72)  # 初始化视角

    '''t-SNE'''
    t0 = time()
    tsne = manifold.TSNE(n_components=n_components, init='pca', random_state=0)
    Y = tsne.fit_transform(X)  # 转换后的输出
    t1 = time()
    print("t-SNE: %.2g sec" % (t1 - t0))  # 算法用时
    ax = fig.add_subplot(2, 1, 2)
    plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
    plt.title("t-SNE (%.2g sec)" % (t1 - t0))
    ax.xaxis.set_major_formatter(NullFormatter())  # 设置标签显示格式为空
    ax.yaxis.set_major_formatter(NullFormatter())
    # plt.axis('tight')
    plt.show()

效果：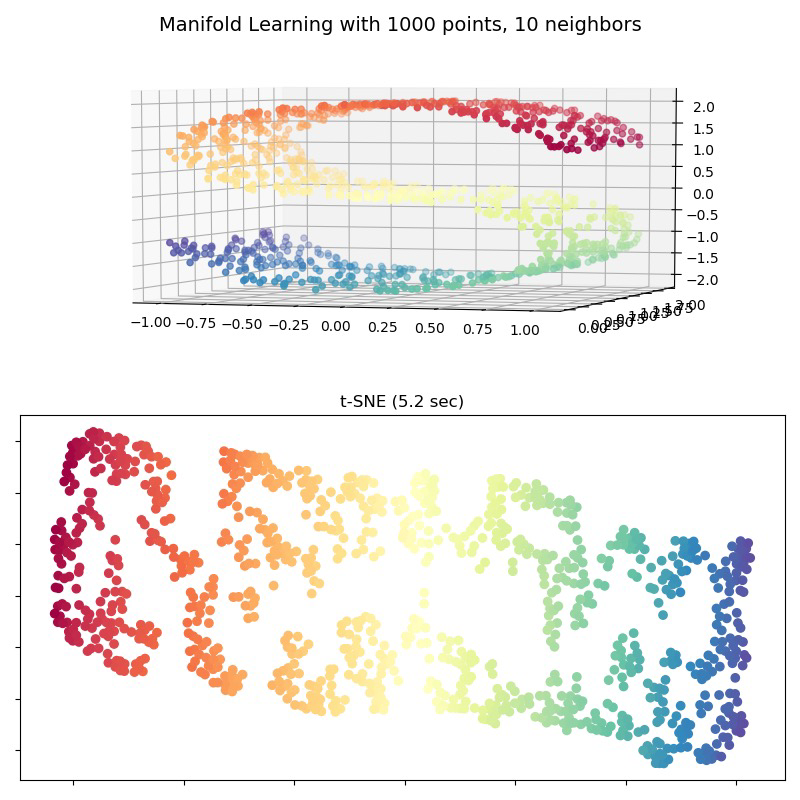

参考文章
Visualizing Data using t-SNE
t-SNE完整笔记
 数据降维与可视化——t-SNE
详解可视化利器 t-SNE 算法：数无形时少直觉
 t-SNE降维原理
 t-SNE：最好的降维方法之一
 从SNE到t-SNE再到LargeVis